Portail d'informations sur la sécurité. Filtrage de Kalman Filtre de Kalman pour les mesures scalaires

Les filtres de Wiener sont les mieux adaptés au traitement de processus ou de segments de processus dans leur ensemble (traitement par blocs). Le traitement séquentiel nécessite une estimation courante du signal à chaque cycle, en tenant compte des informations reçues à l'entrée du filtre lors du processus d'observation.

Avec le filtrage de Wiener, chaque nouvel échantillon de signal nécessiterait un recalcul de tous les poids de filtre. À l'heure actuelle, les filtres adaptatifs sont largement utilisés, dans lesquels les nouvelle information utilisé pour la correction continue d'une estimation de signal précédemment faite (poursuite de cible dans le radar, systèmes de contrôle automatique dans le contrôle, etc.). Les filtres adaptatifs de type récursif, dits filtre de Kalman, sont particulièrement intéressants.

Ces filtres sont largement utilisés dans les boucles de contrôle des systèmes de régulation et de contrôle automatiques. C'est de là qu'ils venaient, comme en témoigne la terminologie spécifique utilisée pour décrire leur travail en tant qu'espace d'état.

L'une des principales tâches à résoudre dans la pratique de l'informatique neuronale est d'obtenir des algorithmes d'apprentissage de réseau neuronal rapides et fiables. A cet égard, il peut être utile d'utiliser un algorithme d'apprentissage de filtres linéaires dans la boucle de rétroaction. Puisque les algorithmes d'apprentissage sont de nature itérative, un tel filtre doit être un estimateur récursif séquentiel.

Problème d'estimation des paramètres

L'un des problèmes de la théorie des solutions statistiques, qui revêt une grande importance pratique, est le problème de l'estimation des vecteurs d'état et des paramètres des systèmes, qui se formule comme suit. Supposons qu'il soit nécessaire d'estimer la valeur du paramètre vectoriel $X$, qui est inaccessible à la mesure directe. Au lieu de cela, un autre paramètre $Z$ est mesuré, en fonction de $X$. La tâche de l'estimation est de répondre à la question : que peut-on dire de $X$ étant donné $Z$ ? Dans le cas général, la procédure d'estimation optimale du vecteur $X$ dépend du critère de qualité accepté pour l'estimation.

Par exemple, l'approche bayésienne du problème d'estimation des paramètres nécessite des informations a priori complètes sur les propriétés probabilistes du paramètre estimé, ce qui est souvent impossible. Dans ces cas, on recourt à la méthode des moindres carrés (LSM), qui nécessite beaucoup moins d'informations a priori.

Considérons l'application des moindres carrés pour le cas où le vecteur d'observation $Z$ est relié au vecteur d'estimation des paramètres $X$ par un modèle linéaire, et qu'il y a un bruit $V$ dans l'observation qui n'est pas corrélé avec le paramètre estimé :

$Z = HX + V$, (1)

où $H$ est la matrice de transformation décrivant la relation entre les valeurs observées et les paramètres estimés.

L'estimation $X$ minimisant l'erreur quadratique s'écrit :

$X_(ots)=(H^TR_V^(-1)H)^(-1)H^TR_V^(-1)Z$, (2)

Soit le bruit $V$ non corrélé, auquel cas la matrice $R_V$ n'est que la matrice identité, et l'équation d'estimation devient plus simple :

$X_(ots)=(H^TH)^(-1)H^TZ$, (3)

L'enregistrement sous forme de matrice permet d'économiser beaucoup de papier, mais peut être inhabituel pour quelqu'un. L'exemple suivant, tiré de la monographie de Yu. M. Korshunov "Mathematical Foundations of Cybernetics", illustre tout cela.
Il y a le circuit électrique suivant :

Les valeurs observées dans ce cas sont les lectures de l'instrument $A_1 ​​​​= 1 A, A_2 = 2 A, V = 20 B$.

De plus, la résistance $R = 5$ Ohm est connue. Il s'agit d'estimer au mieux, du point de vue du critère d'erreur quadratique moyenne minimale, les valeurs des courants $I_1$ et $I_2$. La chose la plus importante ici est qu'il existe une relation entre les valeurs observées (lectures de l'instrument) et les paramètres estimés. Et cette information est apportée de l'extérieur.

Dans ce cas, ce sont les lois de Kirchhoff, dans le cas du filtrage (qui sera discuté plus tard) - un modèle de série chronologique autorégressif, qui suppose que la valeur actuelle dépend des précédentes.

Ainsi, la connaissance des lois de Kirchhoff, qui n'a rien à voir avec la théorie des décisions statistiques, permet d'établir un lien entre les valeurs observées et les paramètres estimés (ceux qui ont étudié l'électrotechnique peuvent vérifier, les autres devront croyez-les sur parole):

$$z_1 = A_1 = I_1 + \xi_1 = 1$$

$$z_2 = A_2 = I_1 + I_2 + \xi_2 = 2$$

$$z_2 = V/R = I_1 + 2 * I_2 + \xi_3 = 4$$

C'est sous forme vectorielle :

$$\begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) \begin(vmatrix) I_1\ \ I_2 \end(vmatrice) + \begin(vmatrice) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrice)$$

Soit $Z = HX + V$, où

$$Z= \begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1\\ 2\\ 4 \end(vmatrix) ; H= \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) ; X= \begin(vmatrix) I_1\\ I_2 \end(vmatrix) ; V= \begin(vmatrice) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrice)$$

En considérant les valeurs de bruit comme non corrélées entre elles, on trouve l'estimation de I 1 et I 2 par la méthode des moindres carrés conformément à la formule 3 :

$H^TH= \begin(vmatrix) 1 & 1& 1\\ 0 & 1& 2 \end(vmatrix) \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) = \ begin(vmatrix) 3 & 3\\ 3 & 5 \end(vmatrix) ; (H^TH)^(-1)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) $;

$H^TZ= \begin(vmatrix) 1 & 1& 1\\ 0 & 1& 2 \end(vmatrix) \begin(vmatrix) 1 \\ 2\\ 4 \end(vmatrix) = \begin(vmatrix) 7\ \ 10 \end(vmatrice) ; X(vmatrix)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) \begin(vmatrix) 7\\ 10 \end(vmatrix) = \frac (1)(6) \begin(vmatrice) 5\\ 9 \end(vmatrice)$ ;

Donc $I_1 = 5/6 = 0,833 A$ ; $I_2 = 9/6 = 1,5 A$.

Tâche de filtrage

Contrairement au problème d'estimation des paramètres qui ont des valeurs fixes, dans le problème de filtration, il est nécessaire d'évaluer les processus, c'est-à-dire de trouver des estimations actuelles d'un signal variant dans le temps déformé par le bruit et, par conséquent, inaccessible à la mesure directe. Dans le cas général, le type d'algorithmes de filtrage dépend des propriétés statistiques du signal et du bruit.

Nous supposerons que le signal utile est une fonction du temps variant lentement et que le bruit est un bruit non corrélé. Nous utiliserons la méthode des moindres carrés, toujours en raison du manque d'information a priori sur les caractéristiques probabilistes du signal et du bruit.

Tout d'abord, nous obtenons une estimation de la valeur actuelle de $x_n$ en utilisant les dernières valeurs $k$ de la série temporelle $z_n, z_(n-1),z_(n-2)\dots z_(n-( k-1))$. Le modèle d'observation est le même que dans le problème d'estimation des paramètres :

Il est clair que $Z$ est un vecteur colonne constitué des valeurs observées de la série temporelle $z_n, z_(n-1),z_(n-2)\dots z_(n-(k-1)) $, $V $ – vecteur colonne de bruit $\xi _n, \xi _(n-1),\xi_(n-2)\dots \xi_(n-(k-1))$, déformant le vrai signal. Et que signifient les symboles $H$ et $X$ ? De quel type de vecteur colonne $X$, par exemple, pouvons-nous parler si tout ce qui est nécessaire est de donner une estimation de la valeur actuelle de la série temporelle ? Et ce que l'on entend par la matrice de transformation $H$ n'est pas du tout clair.

Toutes ces questions ne peuvent être résolues que si le concept d'un modèle de génération de signaux est introduit en considération. C'est-à-dire qu'un modèle du signal d'origine est nécessaire. Cela se comprend, en l'absence d'informations a priori sur les caractéristiques probabilistes du signal et du bruit, il ne reste plus qu'à faire des hypothèses. Vous pouvez appeler cela la divination sur le marc de café, mais les experts préfèrent une terminologie différente. Dans leur sèche-cheveux, cela s'appelle un modèle paramétrique.

Dans ce cas, les paramètres de ce modèle particulier sont estimés. Lors du choix d'un modèle de génération de signal approprié, rappelez-vous que toute fonction analytique peut être étendue dans une série de Taylor. La propriété frappante de la série de Taylor est que la forme d'une fonction à n'importe quelle distance finie $t$ d'un point $x=a$ est uniquement déterminée par le comportement de la fonction dans un voisinage infiniment petit du point $x=a $ (nous parlons de ses dérivées d'ordre premier et supérieur).

Ainsi, l'existence de séries de Taylor signifie que la fonction analytique a une structure interne avec une connexion très forte. Si, par exemple, nous nous limitons à trois membres de la série de Taylor, alors le modèle de génération de signal ressemblera à ceci :

$x_(n-i) = F_(-i)x_n$, (4)

$$X_n= \begin(vmatrix) x_n\\ x"_n\\ x""_n \end(vmatrix) ; F_(-i)= \begin(vmatrix) 1 & -i & i^2/2\\ 0 & 1 & -i\\ 0 & 0 & 1 \end(vmatrice) $$

Autrement dit, la formule 4, avec un ordre donné du polynôme (dans l'exemple, il est égal à 2), établit une connexion entre la $n$-ième valeur du signal dans la séquence temporelle et $(n-i)$-ième . Ainsi, le vecteur d'état estimé comprend dans ce cas, en plus de la valeur estimée elle-même, les dérivées première et seconde du signal.

Dans la théorie de la commande automatique, un tel filtre serait appelé filtre astatique du second ordre. La matrice de transformation $H$ pour ce cas (l'estimation est basée sur les échantillons actuels et $k-1$ précédents) ressemble à ceci :

$$H= \begin(vmatrice) 1 & -k & k^2/2\\ - & - & -\\ 1 & -2 & 2\\ 1 & -1 & 0.5\\ 1 & 0 & 0 \ fin(vmatrice)$$

Tous ces nombres sont obtenus à partir de la série de Taylor, en supposant que l'intervalle de temps entre les valeurs observées adjacentes est constant et égal à 1.

Ainsi, le problème de filtrage, sous nos hypothèses, s'est réduit au problème d'estimation des paramètres ; dans ce cas, les paramètres du modèle de génération de signal adopté par nous sont estimés. Et l'évaluation des valeurs du vecteur d'état $X$ s'effectue selon la même formule 3 :

$$X_(ots)=(H^TH)^(-1)H^TZ$$

En fait, nous avons implémenté un processus d'estimation paramétrique basé sur un modèle autorégressif du processus de génération de signal.

La formule 3 est facilement implémentée dans le logiciel, pour cela vous devez remplir la matrice $H$ et la colonne vectorielle des observations $Z$. Ces filtres sont appelés filtres à mémoire finie, puisqu'ils utilisent les dernières $k$ observations pour obtenir l'estimation actuelle $X_(not)$. À chaque nouvelle étape d'observation, un nouvel ensemble d'observations est ajouté à l'ensemble actuel d'observations et l'ancien est supprimé. Ce processus d'évaluation est appelé fenêtre coulissante.

Filtres de mémoire croissants

Les filtres à mémoire finie ont pour principal inconvénient qu'après chaque nouvelle observation, il est nécessaire de recalculer un recalcul complet de toutes les données stockées en mémoire. De plus, le calcul des estimations ne peut être lancé qu'après avoir cumulé les résultats des premières $k$ observations. C'est-à-dire que ces filtres ont une longue durée du processus transitoire.

Pour pallier cette lacune, il faut passer d'un filtre à mémoire permanente à un filtre à mémoire croissante. Dans un tel filtre, le nombre de valeurs observées à évaluer doit correspondre au nombre n de l'observation courante. Ceci permet d'obtenir des estimations à partir du nombre d'observations égal au nombre de composantes du vecteur estimé $X$. Et cela est déterminé par l'ordre du modèle adopté, c'est-à-dire le nombre de termes de la série de Taylor utilisés dans le modèle.

En même temps, à mesure que n augmente, les propriétés de lissage du filtre s'améliorent, c'est-à-dire que la précision des estimations augmente. Cependant, la mise en œuvre directe de cette approche est associée à une augmentation des coûts de calcul. Par conséquent, les filtres de mémoire croissants sont implémentés comme récurrent.

Le fait est qu'au temps n nous avons déjà l'estimation $X_((n-1)ots)$, qui contient des informations sur toutes les observations précédentes $z_n, z_(n-1), z_(n-2) \dots z_ (n-(k-1))$. L'estimation $X_(not)$ est obtenue par l'observation suivante $z_n$ en utilisant les informations stockées dans l'estimation $X_((n-1))(\mbox (ot))$. Cette procédure est appelée filtrage récurrent et se compose des éléments suivants :

• d'après l'estimation $X_((n-1))(\mbox (ots))$, l'estimation $X_n$ est prédite par la formule 4 pour $i = 1$ : $X_(\mbox (noca priori)) = F_1X_((n-1 )ots)$. Il s'agit d'une estimation a priori ;
• selon les résultats de l'observation courante $z_n$, cette estimation a priori est transformée en vraie, c'est-à-dire a posteriori ;
• cette procédure est répétée à chaque étape, à partir de $r+1$, où $r$ est l'ordre du filtre.

La formule finale de filtrage récursif ressemble à ceci :

$X_((n-1)ots) = X_(\mbox (nocapriori)) + (H^T_nH_n)^(-1)h^T_0(z_n - h_0 X_(\mbox (nocapriori)))$, (6 )

où pour notre filtre de second ordre :

Le filtre de mémoire croissante, qui fonctionne selon la formule 6, est un cas particulier de l'algorithme de filtrage connu sous le nom de filtre de Kalman.

Dans la mise en œuvre pratique de cette formule, il faut se rappeler que l'estimation a priori qui y est incluse est déterminée par la formule 4, et la valeur $h_0 X_(\mbox (nocapriori))$ est la première composante du vecteur $X_( \mbox (pas de capriori))$.

Le filtre de mémoire croissante a une caractéristique importante. En regardant la Formule 6, le score final est la somme du vecteur de score prédit et du terme de correction. Cette correction est importante pour les petits $n$ et diminue lorsque $n$ augmente, tendant vers zéro lorsque $n \rightarrow \infty$. Autrement dit, à mesure que n augmente, les propriétés de lissage du filtre augmentent et le modèle qui y est intégré commence à dominer. Mais le signal réel ne peut correspondre au modèle que sur sections séparées, de sorte que la précision de la prévision se détériore.

Pour lutter contre cela, à partir de quelque $n$, une interdiction est imposée de réduire davantage le terme de correction. Cela équivaut à changer la bande du filtre, c'est-à-dire que pour un petit n, le filtre est plus large bande (moins inertiel), pour un grand n, il devient plus inertiel.

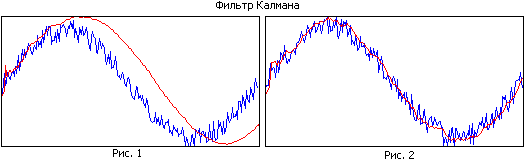
Comparez la figure 1 et la figure 2. Dans la première figure, le filtre a une grande mémoire, alors qu'il lisse bien, mais en raison de la bande étroite, la trajectoire estimée est en retard par rapport à la vraie. Dans la deuxième figure, la mémoire du filtre est plus petite, elle lisse moins bien, mais elle suit mieux la trajectoire réelle.

Littérature

1. Yu.M.Korshunov "Fondements mathématiques de la cybernétique"
2. AVBalakrishnan "Théorie de la filtration de Kalman"
3. V.N. Fomin "Estimation récurrente et filtrage adaptatif"
4. CFN Cowen, P.M. Accorder "Filtres adaptatifs"

Fig. 1

Ainsi, la paire que nous recherchons se situe quelque part sur cette ligne droite. Je le répète, il est impossible de choisir parmi toutes ces options la paire qui a réellement existé - qui a donné le chiffre 12, sans avoir d'indices supplémentaires. Cependant, dans la situation pour laquelle le filtre de Kalman a été inventé, il existe de tels indices. Il y a quelque chose de connu à l'avance sur les nombres aléatoires. En particulier, l'histogramme dit de distribution pour chaque couple de nombres y est connu. Il est généralement obtenu après des observations suffisamment longues des retombées de ces nombres très aléatoires. C'est-à-dire que, par exemple, il est connu par expérience que dans 5 % des cas, la paire x=1, y=8 tombe généralement (nous notons cette paire comme suit : (1,8)), dans 2 % des cas, le couple x=2, y=3 ( 2,3), dans 1% des cas un couple (3,1), dans 0,024% des cas un couple (11,1), etc. Encore une fois, cet histogramme est défini pour tous les couples nombres, y compris ceux qui totalisent 12. Ainsi, pour chaque paire qui totalise 12, on peut dire que, par exemple, la paire (1, 11) tombe dans 0,8 % des cas, la paire ( 2, 10) - dans 1% des cas, paire (3, 9) - dans 1,5% des cas, etc. Ainsi, nous pouvons déterminer à partir de l'histogramme dans quel pourcentage de cas la somme des termes de la paire est 12. Soit, par exemple, dans 30% des cas, la somme donne 12. Et dans les 70% restants, les paires restantes tombent out - ce sont (1.8), (2, 3), (3,1), etc. - ceux qui totalisent des nombres autres que 12. Par ailleurs, supposons par exemple qu'un couple (7,5) tombe dans 27 % des cas, alors que tous les autres couples qui donnent un total de 12 tombent dans 0,024 % + 0,8 % + 1%+1,5%+…=3% des cas. Ainsi, d'après l'histogramme, nous avons découvert que les nombres donnant un total de 12 tombent dans 30% des cas. Dans le même temps, nous savons que si 12 tombe, alors le plus souvent (27% de 30%) la raison en est une paire (7,5). C'est-à-dire si déjà 12 lancé, on peut dire que dans 90% (27% de 30% - ou, ce qui revient au même, 27 fois sur 30) la raison du résultat de 12 est une paire (7,5). Sachant que la paire (7,5) est le plus souvent la raison pour laquelle la somme est égale à 12, il est logique de supposer que, très probablement, elle est tombée maintenant. Bien sûr, ce n'est toujours pas un fait que le nombre 12 est réellement formé par cette paire particulière, cependant, la prochaine fois, si nous rencontrons 12, et nous supposons à nouveau une paire (7,5), alors quelque part dans 90% des cas Nous sommes 100% raison. Mais si nous supposons une paire (2, 10), nous n'aurons raison que 1% de 30% du temps, ce qui équivaut à 3,33% de suppositions correctes contre 90% lorsque nous devinons une paire (7,5). C'est tout - c'est le but de l'algorithme du filtre de Kalman. Autrement dit, le filtre de Kalman ne garantit pas qu'il ne se trompera pas dans la détermination de la somme, mais il garantit qu'il se trompera le nombre minimum de fois (la probabilité d'une erreur sera minime), car il utilise des statistiques - un histogramme de chute de paires de nombres. Il convient également de souligner que la soi-disant densité de distribution de probabilité (PDD) est souvent utilisée dans l'algorithme de filtrage de Kalman. Cependant, il faut bien comprendre que la signification y est la même que celle de l'histogramme. De plus, un histogramme est une fonction construite sur la base de PDF et en étant l'approximation (voir, par exemple, ).
En principe, nous pouvons représenter cet histogramme en fonction de deux variables, c'est-à-dire comme une sorte de surface au-dessus du plan xy. Lorsque la surface est plus élevée, la probabilité que la paire correspondante tombe est également plus élevée. La figure 2 montre une telle surface.

fig.2

Comme vous pouvez le voir, au-dessus de la ligne x + y = 12 (qui sont des variantes de paires donnant un total de 12), il y a des points de surface à différentes hauteurs et la hauteur la plus élevée est dans la variante avec les coordonnées (7,5). Et lorsque l'on tombe sur une somme égale à 12, dans 90% des cas le couple (7,5) est à l'origine de l'apparition de cette somme. Ceux. c'est cette paire, qui totalise 12, qui a la probabilité la plus élevée de se produire, à condition que la somme soit 12.
Ainsi, l'idée derrière le filtre de Kalman est décrite ici. C'est sur lui que toutes sortes de ses modifications sont construites - récurrentes en une seule étape, en plusieurs étapes, etc. Pour une étude plus approfondie du filtre de Kalman, je recommande le livre : Van Tries G. Theory of detection, estimation and modulation.

p.s. Pour ceux qui sont intéressés à expliquer les concepts des mathématiques, ce qu'on appelle "sur les doigts", nous pouvons recommander ce livre et, en particulier, les chapitres de sa section "Mathématiques" (vous pouvez acheter le livre lui-même ou des chapitres individuels de ce).

Une étude a été faite sur l'utilisation du filtre de Kalman dans les développements modernes de systèmes de navigation. Un exemple de construction est donné et analysé modèle mathématique, qui utilise un filtre de Kalman étendu pour améliorer la précision de la détermination des coordonnées des véhicules aériens sans pilote. Le filtre partiel est considéré. Fabriqué bref examen travaux scientifiques utiliser ce filtre pour améliorer la fiabilité et la tolérance aux pannes des systèmes de navigation. Cet article nous permet de conclure que l'utilisation du filtre de Kalman dans les systèmes de positionnement UAV est pratiquée dans de nombreux développements modernes. Il existe un grand nombre de variantes et d'aspects de cette utilisation, qui donnent également des résultats tangibles dans l'amélioration de la précision, notamment en cas de défaillance des systèmes de navigation par satellite standard. C'est le facteur principal de l'influence de cette technologie sur divers domaines scientifiques liés au développement de systèmes de navigation précis et tolérants aux pannes pour divers aéronefs.

Filtre de Kalman

la navigation

véhicule aérien sans pilote (UAV)

1. Makarenko G.K., Alesechkin A.M. Étude de l'algorithme de filtrage pour déterminer les coordonnées d'un objet à partir des signaux des systèmes de radionavigation par satellite Doklady TUSUR. - 2012. - N° 2 (26). - P. 15-18.

2. Bar-Shalom Y., Li X. R., Kirubarajan T. Estimation avec applications

au suivi et à la navigation // Algorithmes théoriques et logiciels. - 2001. - Vol. 3. - P. 10-20.

3. Bassem I.S. Navigation basée sur la vision (VBN) des véhicules aériens sans pilote (UAV) // UNIVERSITÉ DE CALGARY. - 2012. - Vol. 1. - P. 100-127.

4. Conte G., Doherty P. Un système de navigation UAV intégré basé sur la correspondance d'images aériennes // Conférence aérospatiale. - 2008. -Vol. 1. - P. 3142-3151.

5. Guoqiang M., Drake S., Anderson B. Conception d'un filtre de kalman étendu pour la localisation des drones // In Information, Decision and Control. - 2007. - Vol. 7. – P. 224–229.

6. Ponda S.S Trajectory Optimization for Target Localization Using Small Unmanned Aerial Vehicles // Massachusetts Institute of Technology. - 2008. - Vol. 1. - P. 64-70.

7. Wang J., Garrat M., Lambert A. Intégration de capteurs gps/ins/vision pour naviguer dans des véhicules aériens sans pilote // IAPRS&SIS. - 2008. - Vol. 37. – P. 963-969.

L'une des tâches urgentes de la navigation moderne des véhicules aériens sans pilote (UAV) est la tâche d'augmenter la précision de la détermination des coordonnées. Ce problème est résolu en utilisant diverses options d'intégration des systèmes de navigation. L'une des variantes modernes de l'intégration est la combinaison de la navigation gps / glonass avec un filtre de Kalman étendu (Extended Kalmanfilter), estimant de manière récursive la précision à l'aide de mesures incomplètes et bruyantes. Actuellement, diverses variantes du filtre de Kalman étendu existent et sont en cours de développement, y compris un nombre varié de variables d'état. Dans ce travail, nous montrerons à quel point son utilisation peut être efficace dans les développements modernes. Considérons une des représentations caractéristiques d'un tel filtre.

Construire un modèle mathématique

À cet exemple nous ne parlerons que du mouvement du drone dans le plan horizontal, sinon, nous considérerons le problème de localisation dit 2d. Dans notre cas, cela se justifie par le fait que pour de nombreuses situations rencontrées en pratique, le drone peut rester approximativement à la même hauteur. Cette hypothèse est largement utilisée pour simplifier la modélisation de la dynamique des aéronefs. Le modèle dynamique UAV est donné par le système d'équations suivant :

où () - les coordonnées de l'UAV dans le plan horizontal en fonction du temps, de la direction de l'UAV, de la vitesse angulaire de l'UAV et v de la vitesse au sol de l'UAV, fonctionnent et seront considérées comme constantes. Ils sont indépendants les uns des autres, avec des covariances connues et , égales à et , respectivement, et sont utilisées pour simuler les changements d'accélération du drone causés par le vent, les manœuvres du pilote, etc. Les valeurs et sont dérivées de la vitesse angulaire maximale du drone et des valeurs expérimentales des changements de vitesse linéaire du drone, - le symbole de Kronecker.

Ce système d'équations sera approximatif en raison de la non-linéarité du modèle et de la présence de bruit. L'approximation la plus simple dans ce cas est l'approximation d'Euler. Le modèle discret du système de mouvement dynamique UAV est illustré ci-dessous.

vecteur d'état discret du filtre de Kalman, qui permet d'approximer la valeur d'un vecteur d'état continu. ∆ - intervalle de temps entre k et k+1 mesures. () et () - séquences de valeurs de bruit gaussien blanc avec une moyenne nulle. Matrice de covariance pour la première séquence :

De même, pour la deuxième séquence :

Après avoir effectué les substitutions appropriées dans les équations du système (2), on obtient :

Les séquences et sont mutuellement indépendantes. Ce sont également des séquences de bruit gaussien blanc à moyenne nulle avec des matrices de covariance et respectivement. L'avantage de cette forme est qu'elle montre l'évolution du bruit discret entre chaque mesure. En conséquence, nous obtenons le modèle dynamique discret suivant :

(3)

Équation pour :

= + , (4)

où, x et y sont les coordonnées de l'UAV au point de temps k, et est une séquence gaussienne de paramètres aléatoires avec une valeur moyenne nulle, qui est utilisée pour définir l'erreur. Cette séquence est supposée indépendante de () et ().

Les expressions (3) et (4) servent de base pour estimer l'emplacement de l'UAV, où k-ième coordonnées obtenu à l'aide du filtre de Kalman étendu. Modélisation de la défaillance des systèmes de navigation par rapport à ce type filtre montre son efficacité significative.

Pour plus de clarté, nous donnons un petit exemple simple. Laissez un UAV voler uniformément, avec une accélération constante a.

Où, x est la coordonnée de l'UAV au temps t, et δ est une variable aléatoire.

Supposons que nous ayons un capteur GPS qui reçoit des données sur l'emplacement d'un avion. Présentons le résultat de la modélisation de ce processus dans le progiciel MATLAB.

Riz. 1. Filtrage de la lecture du capteur à l'aide du filtre de Kalman

Sur la fig. 1 montre à quel point l'utilisation du filtrage de Kalman peut être efficace.

Cependant, en situation réelle, les signaux présentent souvent une dynamique non linéaire et un bruit anormal. C'est dans de tels cas que le filtre de Kalman étendu est utilisé. Dans le cas où les dispersions de bruit ne sont pas trop importantes (c'est-à-dire qu'une approximation linéaire est adéquate), l'application du filtre de Kalman étendu donne une solution au problème avec une grande précision. Cependant, lorsque le bruit n'est pas gaussien, le filtre de Kalman étendu ne peut pas être appliqué. Dans ce cas, un filtre partiel est généralement utilisé, qui utilise des méthodes numériques pour prendre des intégrales basées sur des méthodes de Monte Carlo avec des chaînes de Markov.

Filtre à particule

Imaginons l'un des algorithmes qui développent les idées du filtre de Kalman étendu - un filtre partiel. Le filtrage partiel est une méthode de filtrage sous-optimale qui fonctionne lors de l'exécution d'une combinaison de Monte Carlo sur un ensemble de particules qui représentent la distribution de probabilité du processus. Ici, une particule est un élément tiré de la distribution a priori du paramètre estimé. L'idée principale d'un filtre partiel est qu'un grand nombre de particules peut être utilisé pour représenter une estimation de distribution. Plus le nombre de particules utilisées est grand, plus l'ensemble de particules représentera avec précision la distribution antérieure. Le filtre à particules est initialisé en y mettant N particules à partir de la distribution a priori des paramètres que l'on veut estimer. L'algorithme de filtrage suppose que ces particules traversent système spécial, puis pondération à l'aide des informations issues de la mesure de ces particules. Les particules résultantes et leurs masses associées représentent la distribution a posteriori du processus d'estimation. Le cycle est répété pour chaque nouvelle mesure et les poids des particules sont mis à jour pour représenter la distribution ultérieure. L'un des principaux problèmes de l'approche traditionnelle du filtrage des particules est que le résultat est généralement quelques particules très lourdes, par opposition à la plupart des autres qui sont très légères. Cela conduit à une instabilité de filtrage. Ce problème peut être résolu en introduisant un taux d'échantillonnage, où N nouvelles particules sont extraites d'une distribution composée d'anciennes particules. Le résultat d'évaluation est obtenu en obtenant un échantillon de la valeur moyenne de la pluralité de particules. Si nous avons plusieurs échantillons indépendants, la moyenne de l'échantillon sera une estimation exacte de la moyenne, définissant la variance finale.

Même si le filtre à particules n'est pas optimal, alors comme le nombre de particules tend vers l'infini, l'efficacité de l'algorithme se rapproche de la règle d'estimation bayésienne. Par conséquent, il est souhaitable d'avoir autant de particules que possible afin d'obtenir meilleur résultat. Malheureusement, cela conduit à une forte augmentation de la complexité des calculs, et, par conséquent, oblige à rechercher un compromis entre précision et rapidité de calcul. Ainsi, le nombre de particules doit être choisi en fonction des exigences du problème d'évaluation de la précision. Un autre facteur important pour le fonctionnement d'un filtre à particules est la limitation du taux d'échantillonnage. Comme mentionné précédemment, le taux d'échantillonnage est un paramètre important de filtrage des particules et sans lui, l'algorithme finira par dégénérer. L'idée est que si les poids sont répartis de manière trop inégale et que le seuil d'échantillonnage est rapidement atteint, les particules de faible poids sont rejetées et l'ensemble restant forme une nouvelle densité de probabilité pour laquelle de nouveaux échantillons peuvent être prélevés. Le choix du seuil de fréquence d'échantillonnage est une tâche assez difficile, car trop haute fréquence rend le filtre trop sensible au bruit, et trop bas donne une grande erreur. Un autre facteur important est la densité de probabilité.

En général, l'algorithme de filtrage des particules montre de bonnes performances de positionnement pour les cibles stationnaires et pour les cibles se déplaçant relativement lentement avec une dynamique d'accélération inconnue. En général, l'algorithme de filtrage des particules est plus stable que le filtre de Kalman étendu et moins sujet à la dégénérescence et aux problèmes graves. En cas de distribution non linéaire, non gaussienne cet algorithme le filtrage montre une très bonne précision de localisation de la cible, tandis que l'algorithme de filtrage de Kalman étendu ne peut pas être utilisé dans de telles conditions. Les inconvénients de cette approche incluent sa plus grande complexité par rapport au filtre de Kalman étendu, ainsi que le fait qu'il n'est pas toujours évident de choisir les bons paramètres pour cet algorithme.

Des recherches prometteuses dans ce domaine

On peut voir dans , l'utilisation d'un modèle de filtre de Kalman similaire à celui que nous avons donné, où il est utilisé pour améliorer les performances d'un système intégré (GPS + modèle de vision par ordinateur pour l'appariement avec une base géographique), et la situation de panne de l'équipement de navigation par satellite est également simulé. Avec l'aide du filtre de Kalman, les résultats du fonctionnement du système en cas de panne ont été considérablement améliorés (par exemple, l'erreur de détermination de la hauteur a été réduite d'environ deux fois et les erreurs de détermination des coordonnées le long de différents axes ont été réduites de près de 9 fois). Une utilisation similaire du filtre de Kalman est également donnée dans .

Un problème intéressant du point de vue d'un ensemble de méthodes est résolu dans . Il utilise également un filtre de Kalman à 5 états, avec quelques différences dans la construction du modèle. Le résultat obtenu dépasse le résultat de notre modèle du fait de l'utilisation de moyens d'intégration supplémentaires (photo et images thermiques sont utilisées). L'application du filtre de Kalman permet dans ce cas de réduire l'erreur de détermination des coordonnées spatiales d'un point donné à une valeur de 5,5 m.

Conclusion

En conclusion, nous notons que l'utilisation du filtre de Kalman dans les systèmes de positionnement UAV est pratiquée dans de nombreux développements modernes. Il existe un grand nombre de variantes et d'aspects de cette utilisation, jusqu'à l'utilisation simultanée de plusieurs filtres similaires avec des facteurs d'état différents. L'un des domaines les plus prometteurs pour le développement des filtres de Kalman est le travail sur la création d'un filtre modifié, dont les erreurs seront représentées par un bruit coloré, ce qui le rendra encore plus précieux pour résoudre des problèmes réels. Un filtre partiel avec lequel un bruit non gaussien peut être filtré est également d'un grand intérêt dans l'art. Cette diversité et des résultats tangibles dans l'amélioration de la précision, notamment en cas de défaillance des systèmes de navigation par satellite standard, sont les principaux facteurs influençant cette technologie dans divers domaines scientifiques liés au développement de systèmes de navigation précis et tolérants aux pannes pour divers aéronefs.

Réviseurs :

Labunets V.G., docteur en sciences techniques, professeur, professeur du département fondements théoriques Radio Engineering Université fédérale de l'Oural du nom du premier président de la Russie B.N. Eltsine, Ekaterinbourg ;

Ivanov V.E., docteur en sciences techniques, professeur, chef. Département de technologie et de communication, Université fédérale de l'Oural du nom du premier président de la Russie B.N. Eltsine, Ekaterinbourg.

Lien bibliographique

Random Forest est l'un de mes algorithmes d'exploration de données préférés. Premièrement, il est incroyablement polyvalent, il peut être utilisé pour résoudre à la fois des problèmes de régression et de classification. Recherchez des anomalies et sélectionnez des prédicteurs. Deuxièmement, il s'agit d'un algorithme très difficile à appliquer de manière incorrecte. Tout simplement parce que, contrairement à d'autres algorithmes, il possède peu de paramètres personnalisables. Et pourtant, il est étonnamment simple dans son essence. En même temps, il est remarquablement précis.

Quelle est l'idée d'un algorithme aussi merveilleux? L'idée est simple : disons que nous avons un algorithme très faible, disons . Si nous créons de nombreux modèles différents à l'aide de cet algorithme faible et que nous calculons la moyenne du résultat de leurs prédictions, le résultat final sera bien meilleur. C'est ce qu'on appelle l'apprentissage d'ensemble en action. L'algorithme Random Forest est donc appelé "Random Forest", pour les données reçues il crée de nombreux arbres de décision puis fait la moyenne du résultat de leurs prédictions. Un point important ici est l'élément aléatoire dans la création de chaque arbre. Après tout, il est clair que si nous créons de nombreux arbres identiques, le résultat de leur moyenne aura la précision d'un arbre.

Comment travaille-t-il ? Supposons que nous ayons des données d'entrée. Chaque colonne correspond à un paramètre, chaque ligne correspond à un élément de données.

Nous pouvons choisir, au hasard, un certain nombre de colonnes et de lignes dans l'ensemble de données et construire un arbre de décision à partir de celles-ci.

jeudi 10 mai 2012

jeudi 12 janvier 2012

Tout a commencé en avril 2011 lorsque j'ai eu un entretien téléphonique avec Zynga. Ensuite, tout cela ressemblait à une sorte de jeu qui n'avait rien à voir avec la réalité, et je ne pouvais même pas imaginer à quoi cela mènerait. En juin 2011, Zynga est arrivé à Moscou et a mené une série d'entretiens, environ 60 candidats ayant réussi un entretien téléphonique ont été pris en compte et environ 15 personnes ont été sélectionnées parmi eux (je ne connais pas le nombre exact, quelqu'un a changé d'avis plus tard, quelqu'un a immédiatement refusé). L'interview s'est avérée étonnamment simple. Aucune tâche de programmation pour vous, aucune question complexe sur la forme des hachures, principalement la possibilité de discuter a été testée. Et la connaissance, à mon avis, n'a été évaluée que superficiellement.

Et puis le galimatias a commencé. Nous avons d'abord attendu les résultats, puis l'offre, puis l'approbation du LCA, puis l'approbation de la demande de visa, puis les documents des États-Unis, puis la ligne à l'ambassade, puis le contrôle supplémentaire, puis le visa. Parfois, il m'a semblé que j'étais prêt à tout lâcher et à marquer. Parfois, j'ai douté que nous ayons besoin de cette Amérique, car la Russie n'est pas mal non plus. L'ensemble du processus a pris environ six mois, à la fin, à la mi-décembre, nous avons reçu des visas et avons commencé à préparer le départ.

Lundi était mon premier jour au nouveau travail. Le bureau a toutes les conditions non seulement pour travailler, mais aussi pour vivre. Petits déjeuners, déjeuners et dîners de nos propres chefs, un tas de plats variés farcis dans tous les coins, une salle de sport, des massages et même un coiffeur. Tout cela est entièrement gratuit pour les employés. Beaucoup se rendent au travail à vélo et plusieurs salles sont équipées pour entreposer les véhicules. En général, je n'ai jamais rien vu de tel en Russie. Cependant, tout a son prix, nous avons tout de suite été prévenus que nous devions beaucoup travailler. Ce qui est "beaucoup", selon leurs normes, n'est pas très clair pour moi.

J'espère cependant que malgré la quantité de travail, dans un avenir prévisible, je pourrai reprendre le blog et peut-être raconter quelque chose sur la vie américaine et le travail de programmeur en Amérique. Attend et regarde. En attendant, je vous souhaite à tous un Joyeux Noël et une Bonne Année et à bientôt !

résultat<- NULL for(i in (1:length(divs[,1]))){ d <- divs if (d$Divs>0)( essayer(( guillemets<- getSymbols(d$Symbol, src="Finam", from="2010-01-01", auto.assign=FALSE) if (!is.nan(quotes)){ price <- Cl(quotes) if (length(price)>0)(jj<- d$Divs result <- rbind(result, data.frame(d$Symbol, d$Name, d$RegistryDate, as.numeric(dd)/as.numeric(price), stringsAsFactors=FALSE)) } } }, silent=TRUE) } } colnames(result) <- c("Symbol", "Name", "RegistryDate", "Divs") result

Sur Internet, y compris Habré, vous pouvez trouver de nombreuses informations sur le filtre de Kalman. Mais il est difficile de trouver une dérivation facilement digestible des formules elles-mêmes. Sans conclusion, toute cette science est perçue comme une sorte de chamanisme, les formules ressemblent à un ensemble de symboles sans visage et, plus important encore, de nombreuses déclarations simples qui se trouvent à la surface de la théorie sont incompréhensibles. Le but de cet article sera de parler de ce filtre dans le langage le plus accessible.
Le filtre de Kalman est un puissant outil de filtrage des données. Son principe principal est que lors du filtrage, des informations sur la physique du phénomène lui-même sont utilisées. Disons que si vous filtrez les données du compteur de vitesse d'une voiture, l'inertie de la voiture vous donne le droit de percevoir des sauts de vitesse trop rapides comme une erreur de mesure. Le filtre de Kalman est intéressant car, en un sens, c'est le meilleur filtre. Nous discuterons plus en détail ci-dessous de ce que signifient exactement les mots "le meilleur". A la fin de l'article, je montrerai que dans de nombreux cas les formules peuvent être simplifiées à tel point qu'il n'en reste presque plus rien.

Likbez

Avant de me familiariser avec le filtre de Kalman, je propose de rappeler quelques définitions et faits simples issus de la théorie des probabilités.

Valeur aléatoire

Quand ils disent qu'une variable aléatoire est donnée, ils veulent dire que cette variable peut prendre des valeurs aléatoires. Il prend différentes valeurs avec différentes probabilités. Lorsque vous lancez, disons, un dé, un ensemble discret de valeurs tombera : . Quand il s'agit, par exemple, de la vitesse d'une particule errante, alors, évidemment, on doit faire face à un ensemble continu de valeurs. Les valeurs "abandonnées" d'une variable aléatoire seront désignées par , mais parfois nous utiliserons la même lettre qui désigne une variable aléatoire : .
Dans le cas d'un ensemble continu de valeurs, la variable aléatoire est caractérisée par la densité de probabilité , qui nous dicte que la probabilité que la variable aléatoire "tombe" dans un petit voisinage d'un point de longueur est égale à . Comme on peut le voir sur l'image, cette probabilité est égale à l'aire du rectangle grisé sous le graphique :

Assez souvent dans la vie, les variables aléatoires sont distribuées selon Gauss, lorsque la densité de probabilité est .

On voit que la fonction a la forme d'une cloche centrée en un point et de largeur caractéristique de l'ordre de .
Puisque nous parlons de la distribution gaussienne, ce serait un péché de ne pas mentionner d'où elle vient. Tout comme les nombres sont solidement ancrés dans les mathématiques et apparaissent aux endroits les plus inattendus, la distribution gaussienne s'est profondément enracinée dans la théorie des probabilités. Une déclaration remarquable qui explique en partie l'omniprésence gaussienne est la suivante :
Soit une variable aléatoire ayant une distribution arbitraire (en fait, il existe certaines restrictions à cet arbitraire, mais elles ne sont pas du tout rigides). Réalisons des expériences et calculons la somme des valeurs "abandonnées" d'une variable aléatoire. Faisons beaucoup de ces expériences. Il est clair que nous recevrons à chaque fois une valeur différente de la somme. En d'autres termes, cette somme est en elle-même une variable aléatoire avec sa propre loi de distribution. Il s'avère que pour suffisamment grand, la loi de distribution de cette somme tend vers la distribution gaussienne (d'ailleurs, la largeur caractéristique de la « cloche » croît comme ). En savoir plus sur wikipedia : théorème central limite. Dans la vie, il y a très souvent des quantités composées d'un grand nombre de variables aléatoires indépendantes également réparties, et donc distribuées selon Gauss.

Moyenne

La valeur moyenne d'une variable aléatoire est ce que nous obtenons dans la limite si nous menons de nombreuses expériences et calculons la moyenne arithmétique des valeurs supprimées. La valeur moyenne est désignée de différentes manières : les mathématiciens aiment désigner par (espérance) et les mathématiciens étrangers par (espérance). Physique même à travers ou. On désignera de façon étrangère :.
Par exemple, pour une distribution gaussienne , la moyenne est .

Dispersion

Dans le cas de la distribution gaussienne, nous pouvons clairement voir que la variable aléatoire préfère tomber dans un voisinage de sa valeur moyenne . Comme on peut le voir sur le graphique, la dispersion caractéristique des valeurs de commande est . Comment estimer cet étalement de valeurs pour une variable aléatoire arbitraire si on connaît sa distribution. Vous pouvez tracer un graphique de sa densité de probabilité et estimer la largeur caractéristique à l'œil nu. Mais nous préférons suivre la voie algébrique. Vous pouvez trouver la longueur moyenne de l'écart (module) par rapport à la valeur moyenne : . Cette valeur sera une bonne estimation de la dispersion caractéristique des valeurs. Mais vous et moi savons très bien que l'utilisation de modules dans les formules est un casse-tête, donc cette formule est rarement utilisée pour estimer la propagation caractéristique.
Un moyen plus simple (simple en termes de calculs) est de trouver . Cette quantité s'appelle la variance et est souvent appelée . La racine de la variance s'appelle l'écart-type. L'écart-type est une bonne estimation de la propagation d'une variable aléatoire.
Par exemple, pour une distribution gaussienne, on peut supposer que la variance définie ci-dessus est exactement égale à , ce qui signifie que l'écart type est égal à , ce qui s'accorde très bien avec notre intuition géométrique.
En fait, il y a une petite arnaque cachée ici. Le fait est que dans la définition de la distribution gaussienne, sous l'exposant se trouve l'expression . Ce deux au dénominateur est précisément pour que l'écart type soit égal au coefficient. C'est-à-dire que la formule de distribution gaussienne elle-même est écrite sous une forme spécialement affinée pour le fait que nous allons considérer son écart type.

Variables aléatoires indépendantes

Les variables aléatoires peuvent être dépendantes ou non. Imaginez que vous jetez une aiguille dans un avion et notez les coordonnées de ses deux extrémités. Ces deux coordonnées sont dépendantes, elles sont reliées par la condition que la distance entre elles soit toujours égale à la longueur de l'aiguille, bien qu'il s'agisse de variables aléatoires.
Les variables aléatoires sont indépendantes si le résultat de la première est complètement indépendant du résultat de la seconde. Si les variables aléatoires et sont indépendantes, alors la valeur moyenne de leur produit est égale au produit de leurs valeurs moyennes :

Preuve

Par exemple, avoir les yeux bleus et terminer ses études avec une médaille d'or sont des variables aléatoires indépendantes. Si aux yeux bleus, disons médaillés d'or , alors médaillés aux yeux bleus Cet exemple nous dit que si les variables aléatoires et sont données par leurs densités de probabilité et , alors l'indépendance de ces quantités s'exprime dans le fait que la densité de probabilité (la première valeur abandonnée , et la seconde ) est trouvée par la formule :

Il en résulte immédiatement que :

Comme vous pouvez le voir, la preuve est effectuée pour des variables aléatoires qui ont un spectre continu de valeurs et sont données par leur densité de probabilité. Dans d'autres cas, l'idée de la preuve est similaire.

Filtre de Kalman

Formulation du problème

Désignons par la valeur que nous allons mesurer puis filtrer. Il peut s'agir de coordonnées, de vitesse, d'accélération, d'humidité, de degré de puanteur, de température, de pression, etc.
Commençons par un exemple simple, qui nous conduira à la formulation d'un problème général. Imaginez que nous ayons une voiture radiocommandée qui ne peut qu'avancer et reculer. Nous, connaissant le poids de la voiture, sa forme, la surface de la route, etc., avons calculé comment le joystick de contrôle affecte la vitesse de déplacement.

Ensuite, la coordonnée de la machine changera conformément à la loi :

Dans la vraie vie, nous ne pouvons pas prendre en compte dans nos calculs les petites perturbations agissant sur la voiture (vent, bosses, cailloux sur la route), donc la vitesse réelle de la voiture sera différente de celle calculée. Une variable aléatoire est ajoutée au côté droit de l'équation écrite :

Nous avons un capteur GPS installé sur la voiture, qui essaie de mesurer la véritable coordonnée de la voiture et, bien sûr, ne peut pas la mesurer exactement, mais la mesure avec une erreur, qui est également une variable aléatoire. En conséquence, nous obtenons des données erronées du capteur :

Le problème est que, connaissant les lectures incorrectes du capteur, trouvez une bonne approximation de la vraie coordonnée de la machine.
Dans la formulation du problème général, tout peut être responsable de la coordonnée (température, humidité ...), et nous désignerons le terme responsable du contrôle du système de l'extérieur par (dans l'exemple avec la machine). Les équations pour les relevés de coordonnées et de capteurs ressembleront à ceci :

Discutons en détail de ce que nous savons :

Il est utile de noter que la tâche de filtrage n'est pas une tâche de lissage. Nous ne visons pas à lisser les données du capteur, nous visons à obtenir la valeur la plus proche de la coordonnée réelle.

Algorithme de Kalman

On raisonnera par induction. Imaginez qu'à la -ième étape nous ayons déjà trouvé la valeur filtrée du capteur, qui se rapproche bien de la vraie coordonnée du système. N'oubliez pas que nous connaissons l'équation qui contrôle le changement d'une coordonnée inconnue :

par conséquent, sans obtenir encore la valeur du capteur, nous pouvons supposer qu'à l'étape où le système évolue selon cette loi, le capteur affichera quelque chose de proche de . Malheureusement, nous ne pouvons encore rien dire de plus précis. D'autre part, à l'étape, nous aurons une lecture de capteur inexacte sur nos mains.
L'idée de Kalman est la suivante. Pour obtenir la meilleure approximation de la vraie coordonnée, nous devons choisir un juste milieu entre la lecture inexacte du capteur et notre prédiction de ce que nous nous attendions à voir. Nous donnerons un poids à la lecture du capteur et la valeur prédite aura un poids :

Le coefficient est appelé coefficient de Kalman. Cela dépend du pas d'itération, il serait donc plus correct d'écrire , mais pour l'instant, afin de ne pas encombrer les formules de calcul, nous allons omettre son indice.
Nous devons choisir le coefficient de Kalman de manière à ce que la valeur optimale résultante de la coordonnée soit la plus proche de la vraie valeur. Par exemple, si nous savons que notre capteur est très précis, alors nous ferons davantage confiance à sa lecture et donnerons plus de poids à la valeur (proche de un). Si le capteur, au contraire, n'est pas du tout précis, alors nous nous concentrerons davantage sur la valeur théoriquement prédite de .
En général, pour trouver la valeur exacte du coefficient de Kalman, il suffit de minimiser l'erreur :

Nous utilisons les équations (1) (celles de la case bleue) pour réécrire l'expression de l'erreur :

Preuve

Il est maintenant temps de discuter de ce que signifie l'expression minimiser l'erreur ? Après tout, l'erreur, comme on le voit, est elle-même une variable aléatoire et prend à chaque fois des valeurs différentes. Il n'y a vraiment pas d'approche unique pour définir ce que signifie que l'erreur soit minimale. Comme dans le cas de la variance d'une variable aléatoire, lorsque l'on a essayé d'estimer la largeur caractéristique de sa dispersion, on choisira ici le critère de calcul le plus simple. Nous allons minimiser la moyenne de l'erreur quadratique :

Écrivons la dernière expression :

Preuve

Du fait que toutes les variables aléatoires incluses dans l'expression de sont indépendantes, il s'ensuit que tous les termes "croisés" sont égaux à zéro :

Nous avons utilisé le fait que , alors la formule de la variance semble beaucoup plus simple : .

Cette expression prend une valeur minimale lorsque (égaliser la dérivée à zéro) :

Ici, nous écrivons déjà une expression pour le coefficient de Kalman avec l'indice de pas , nous soulignons donc qu'il dépend du pas d'itération.
Nous substituons la valeur optimale obtenue dans l'expression pour laquelle nous avons minimisé. Nous recevons;

Notre tâche est résolue. Nous avons obtenu une formule itérative pour calculer le coefficient de Kalman.
Résumons nos connaissances acquises dans un cadre :

Exemple

Code Matlab

tout effacer; N=100% nombre d'échantillons a=0,1% accélération sigmaPsi=1 sigmaEta=50 ; k=1:N x=k x(1)=0 z(1)=x(1)+normrnd(0,sigmaEta); pour t=1 :(N-1) x(t+1)=x(t)+a*t+normrnd(0,sigmaPsi) ; z(t+1)=x(t+1)+normrnd(0,sigmaEta); fin; %filtre de kalman xOpt(1)=z(1); eOpt(1) = sigmaEta ; pour t=1 :(N-1) eOpt(t+1)=sqrt((sigmaEta^2)*(eOpt(t)^2+sigmaPsi^2)/(sigmaEta^2+eOpt(t)^2+ sigmaPsi^2)) K(t+1)=(eOpt(t+1))^2/sigmaEta^2 xOpt(t+1)=(xOpt(t)+a*t)*(1-K(t +1))+K(t+1)*z(t+1) fin ; plot(k,xopt,k,z,k,x)

Une analyse

Si nous suivons comment le coefficient de Kalman change avec l'étape d'itération, nous pouvons montrer qu'il se stabilise toujours à une certaine valeur. Par exemple, lorsque les erreurs RMS du capteur et du modèle sont liées l'une à l'autre comme dix pour un, le tracé du coefficient de Kalman en fonction de l'étape d'itération ressemble à ceci :

Dans l'exemple suivant, nous verrons comment cela peut rendre nos vies beaucoup plus faciles.

Deuxième exemple

En pratique, il arrive souvent que nous ne sachions rien du tout sur le modèle physique de ce que nous filtrons. Par exemple, vous souhaitez filtrer les lectures de votre accéléromètre préféré. Vous ne savez pas à l'avance selon quelle loi vous comptez faire tourner l'accéléromètre. La plupart des informations que vous pouvez glaner sont la variance d'erreur du capteur. Dans une situation aussi difficile, toute ignorance du modèle de mouvement peut être ramenée à une variable aléatoire :

Mais, franchement, un tel système ne satisfait plus les conditions que nous avons imposées à la variable aléatoire , car maintenant toute la physique du mouvement qui nous est inconnue s'y cache, et donc on ne peut pas dire qu'à différents moments du temps, les erreurs de la modèle sont indépendants les uns des autres et que leurs valeurs moyennes sont nulles. Dans ce cas, en gros, la théorie du filtre de Kalman n'est pas applicable. Mais, nous ne ferons pas attention à ce fait, mais, appliquons bêtement tout le colosse de formules, en choisissant les coefficients et à l'œil, pour que les données filtrées soient jolies.
Mais il y a une autre façon beaucoup plus simple de procéder. Comme nous l'avons vu plus haut, le coefficient de Kalman se stabilise toujours à la valeur . Par conséquent, au lieu de sélectionner les coefficients et de trouver le coefficient de Kalman à l'aide de formules complexes, nous pouvons considérer ce coefficient comme étant toujours une constante et ne sélectionner que cette constante. Cette hypothèse ne gâchera presque rien. Premièrement, nous utilisons déjà illégalement la théorie de Kalman, et deuxièmement, le coefficient de Kalman se stabilise rapidement à une constante. Au final, tout sera très simple. Nous n'avons pas du tout besoin de formules de la théorie de Kalman, nous avons juste besoin de choisir une valeur acceptable et de l'insérer dans la formule itérative :

Le graphique suivant montre les données d'un capteur fictif filtrées de deux manières différentes. A condition de ne rien savoir de la physique du phénomène. La première voie est honnête, avec toutes les formules de la théorie de Kalman. Et le second est simplifié, sans formules.

Comme nous pouvons le voir, les méthodes sont presque les mêmes. Une petite différence n'est observée qu'au début, lorsque le coefficient de Kalman n'est pas encore stabilisé.

Discussion

Comme nous l'avons vu, l'idée principale du filtre de Kalman est de trouver un coefficient tel que la valeur filtrée

en moyenne différerait le moins de la valeur réelle de la coordonnée . Nous voyons que la valeur filtrée est une fonction linéaire de la lecture du capteur et de la valeur filtrée précédente. Et la valeur filtrée précédente est, à son tour, une fonction linéaire de la lecture du capteur et de la valeur filtrée précédente. Et ainsi de suite, jusqu'à ce que la chaîne soit complètement déroulée. Autrement dit, la valeur filtrée dépend de tout lectures précédentes du capteur linéairement :

Par conséquent, le filtre de Kalman est appelé filtre linéaire.
On peut prouver que le filtre de Kalman est le meilleur de tous les filtres linéaires. Le meilleur dans le sens où le carré moyen de l'erreur de filtre est minime.

Cas multivarié

Toute la théorie du filtre de Kalman peut être généralisée au cas multidimensionnel. Les formules y semblent un peu plus effrayantes, mais l'idée même de leur dérivation est la même que dans le cas unidimensionnel. Vous pouvez les voir dans cet excellent article : http://habrahabr.ru/post/140274/ .
Et dans ce merveilleux vidéo un exemple de comment les utiliser.