Drošības informācijas portāls. Kalmana filtrēšana Kalmana filtrs skalārajiem mērījumiem

Wiener filtri ir vislabāk piemēroti apstrādes procesiem vai procesu sekcijām kopumā (bloku apstrādei). Secīgai apstrādei nepieciešams pašreizējais signāla novērtējums katrā pulksteņa ciklā, ņemot vērā informāciju, kas saņemta filtra ieejā novērošanas procesa laikā.

Izmantojot Vīnera filtrēšanu, katram jaunam signāla paraugam būtu jāpārrēķina visi filtra svara koeficienti. Šobrīd adaptīvie filtri, kuros ienākošie jaunu informāciju izmanto iepriekš veiktā signāla novērtējuma nepārtrauktai regulēšanai (mērķa izsekošana radarā, automātiskās vadības sistēmas kontrolē utt.). Īpaši interesanti ir adaptīvie rekursīvie filtri, kas pazīstami kā Kalmana filtrs.

Šos filtrus plaši izmanto automātiskās regulēšanas un vadības sistēmu vadības cilpās. Lūk, no kurienes viņi nāca, par ko liecina īpašā terminoloģija, ko izmanto, lai aprakstītu viņu darbu kā valsts telpu.

Viena no galvenajām problēmām, kas jāatrisina neironu skaitļošanas praksē, ir ātru un uzticamu algoritmu iegūšana neironu tīklu apmācībai. Šajā sakarā var būt lietderīgi atgriezeniskās saites cilpā izmantot lineāro filtru apmācības algoritmu. Tā kā mācību algoritmi pēc būtības ir iteratīvi, šādam filtram ir jābūt secīgam rekursīvam novērtētājam.

Parametru novērtēšanas problēma

Viena no statistisko risinājumu teorijas problēmām, kam ir liela praktiska nozīme, ir stāvokļu vektoru un sistēmu parametru novērtēšanas problēma, kas formulēta šādi. Pieņemsim, ka ir nepieciešams novērtēt vektora parametra $X$ vērtību, kas nav tieši izmērāms. Tā vietā tiek mērīts cits parametrs $Z$ atkarībā no $X$. Novērtējuma uzdevums ir atbildēt uz jautājumu: ko var teikt par $X$, zinot $Z$. Kopumā vektora $X$ optimālās novērtēšanas procedūra ir atkarīga no pieņemtā vērtējuma kvalitātes kritērija.

Piemēram, Bajesa pieeja parametru novērtēšanas problēmai prasa pilnīgu a priori informāciju par novērtētā parametra varbūtības īpašībām, kas bieži vien nav iespējams. Šādos gadījumos viņi izmanto mazāko kvadrātu metodi (LSM), kas prasa ievērojami mazāk a priori informācijas.

Apskatīsim mazāko kvadrātu pielietojumu gadījumam, kad novērojuma vektors $Z$ ir saistīts ar parametra novērtējuma vektoru $X$ ar lineāro modeli, un novērojumā ir troksnis $V$, kas nav korelēts ar aprēķināto parametru:

$Z = HX + V$, (1)

kur $H$ ir transformācijas matrica, kas apraksta saistību starp novērotajiem daudzumiem un aprēķinātajiem parametriem.

Aprēķinu $X$, kas samazina kļūdu kvadrātā, raksta šādi:

$X_(ots)=(H^TR_V^(-1)H)^(-1)H^TR_V^(-1)Z$, (2)

Lai troksnis $V$ ir nekorelēts, un tādā gadījumā matrica $R_V$ ir vienkārši identitātes matrica, un novērtējuma vienādojums kļūst vienkāršāks:

$X_(ots)=(H^TH)^(-1)H^TZ$, (3)

Rakstīšana matricas formā ietaupa daudz papīra, taču dažiem tas var būt neparasti. To visu ilustrē šāds piemērs, kas ņemts no Ju. M. Koršunova monogrāfijas “Kibernētikas matemātiskie pamati”.
Ir šāda elektriskā ķēde:

Novērotie lielumi šajā gadījumā ir instrumenta rādījumi $A_1 ​​= 1 A, A_2 = 2 A, V = 20 B$.

Turklāt ir zināms, ka pretestība ir $ R = 5 $ Ohm. No minimālās vidējās kvadrātiskās kļūdas kritērija viedokļa vislabākajā veidā ir jānovērtē strāvu $I_1$ un $I_2$ vērtības. Vissvarīgākais šeit ir tas, ka starp novērotajiem daudzumiem (instrumentu rādījumiem) un aprēķinātajiem parametriem ir kāda saistība. Un šī informācija tiek ienesta no ārpuses.

Šajā gadījumā tie ir Kirhhofa likumi, filtrēšanas gadījumā (kas tiks apspriests vēlāk) - laika rindas autoregresīvs modelis, kas pieņem pašreizējās vērtības atkarību no iepriekšējām.

Tātad Kirhofa likumu zināšanas, kas nekādā veidā nav saistītas ar statistisko risinājumu teoriju, ļauj mums izveidot saikni starp novērotajām vērtībām un aprēķinātajiem parametriem (tie, kas ir studējuši elektrotehniku, var pārbaudīt, pārējie būs lai pieņemtu viņu vārdus):

$$z_1 = A_1 = I_1 + \xi_1 = 1 $$

$$z_2 = A_2 = I_1 + I_2 + \xi_2 = 2 $$

$$z_2 = V/R = I_1 + 2 * I_2 + \xi_3 = 4 $$

Tas ir vektora formā:

$$\begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) \begin(vmatrix) I_1\ \ I_2 \end(vmatrix) + \begin(vmatrix) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrix)$$

Vai $Z = HX + V$, kur

$$Z= \begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1\\ 2\\ 4 \end(vmatrix) ; H= \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) ; X= \begin(vmatrix) I_1\\ I_2 \end(vmatrix) ; V= \begin(vmatrix) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrix)$$

Ņemot vērā, ka trokšņa vērtības nav savstarpēji saistītas, mēs atradīsim I 1 un I 2 novērtējumu, izmantojot mazāko kvadrātu metodi saskaņā ar 3. formulu:

$H^TH= \begin(vmatrix) 1 & 1& 1\\ 0 & 1& 2 \end(vmatrix) \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) = \ begin(vmatrix) 3 & 3\\ 3 & 5 \end(vmatrix) ; (H^TH)^(-1)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) $;

$H^TZ= \begin(vmatrix) 1 & 1& 1\\ 0 & 1& 2 \end(vmatrix) \begin(vmatrix) 1 \\ 2\\ 4 \end(vmatrix) = \begin(vmatrix) 7\ \ 10 \end(vmatrix) ; X(ots)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) \begin(vmatrix) 7\\ 10 \end(vmatrix) = \frac (1) (6) \begin(vmatrix) 5\\ 9 \end(vmatrix)$;

Tātad $I_1 = 5/6 = 0,833 A$; I_2 $ = 9/6 = 1,5 A$.

Filtrēšanas uzdevums

Atšķirībā no parametru, kuriem ir fiksētas vērtības, novērtēšanas problēmas, filtrēšanas problēmai ir nepieciešami novērtēšanas procesi, tas ir, atrast pašreizējos aprēķinus par laikā mainīgu signālu, kas ir izkropļots ar troksni un tāpēc nav pieejams tiešam mērījumam. Kopumā filtrēšanas algoritmu veids ir atkarīgs no signāla un trokšņa statistiskajām īpašībām.

Mēs pieņemsim, ka noderīgais signāls ir lēni mainīga laika funkcija, un traucējumi ir nekorelēts troksnis. Mēs izmantosim mazāko kvadrātu metodi, atkal tāpēc, ka trūkst a priori informācijas par signāla un trokšņa varbūtības raksturlielumiem.

Pirmkārt, mēs iegūstam pašreizējās vērtības $x_n$ aprēķinu, pamatojoties uz pieejamajām $k$ jaunākajām vērtībām laikrindā $z_n, z_(n-1),z_(n-2)\dots z_(n- (k-1))$. Novērošanas modelis ir tāds pats kā parametru novērtēšanas uzdevumā:

Ir skaidrs, ka $Z$ ir kolonnas vektors, kas sastāv no novērotajām laikrindu vērtībām $z_n, z_(n-1),z_(n-2)\dots z_(n-(k-1))$ , $V $ ir trokšņu kolonnas vektors $\xi _n, \xi _(n-1),\xi_(n-2)\dots \xi _(n-(k-1))$, izkropļojot patieso signālu. . Ko nozīmē simboli $H$ un $X$? Par ko, piemēram, kolonnas vektoru $X$ var runāt, ja atliek vien novērtēt laikrindas pašreizējo vērtību? Un kas ir domāts ar transformācijas matricu $H$, parasti nav skaidrs.

Uz visiem šiem jautājumiem var atbildēt tikai tad, ja tiek ņemta vērā signāla ģenerēšanas modeļa koncepcija. Tas ir, ir nepieciešams kāds sākotnējā signāla modelis. Tas ir saprotams; ja nav a priori informācijas par signāla un traucējumu varbūtības raksturlielumiem, var izdarīt tikai pieņēmumus. To var saukt par zīlēšanu uz kafijas biezumiem, taču eksperti dod priekšroku citai terminoloģijai. Viņu fēnā to sauc par parametrisko modeli.

Šajā gadījumā tiek aprēķināti šī konkrētā modeļa parametri. Izvēloties piemērotu signālu ģenerēšanas modeli, atcerieties, ka jebkuru analītisko funkciju var paplašināt Taylor sērijā. Teilora sērijas pārsteidzoša īpašība ir tāda, ka funkcijas formu jebkurā ierobežotā attālumā $t$ no noteikta punkta $x=a$ unikāli nosaka funkcijas darbība bezgalīgi mazā punkta $x=a apkārtnē. $ (mēs runājam par tā pirmās un augstākās kārtas atvasinājumiem).

Tādējādi Teilora sērijas esamība nozīmē, ka analītiskajai funkcijai ir iekšēja struktūra ar ļoti spēcīgu savienojumu. Ja, piemēram, mēs aprobežojamies ar trim Teilora sērijas terminiem, signāla ģenerēšanas modelis izskatīsies šādi:

$x_(n-i) = F_(-i)x_n$, (4)

$$X_n= \begin(vmatrix) x_n\\ x"_n\\ x""_n \end(vmatrix) ; F_(-i)= \begin(vmatrix) 1 & -i & i^2/2\\ 0 & 1 & -i\\ 0 & 0 & 1 \end(vmatrix) $$

Tas ir, formula 4 noteiktai polinoma secībai (piemērā tas ir vienāds ar 2) izveido savienojumu starp signāla $n$-to vērtību laika secībā un $(n-i)$-. th. Tādējādi aprēķinātais stāvokļa vektors šajā gadījumā papildus pašai aprēķinātajai vērtībai ietver signāla pirmo un otro atvasinājumu.

Automātiskās vadības teorijā šādu filtru varētu saukt par filtru ar 2. kārtas astatismu. Transformācijas matrica $H$ šim gadījumam (novērtēta, izmantojot pašreizējos un $k-1$ iepriekšējos paraugus) izskatās šādi:

$$H= \begin(vmatrix) 1 & -k & k^2/2\\ - & - & -\\ 1 & -2 & 2\\ 1 & -1 & 0.5\\ 1 & 0 & 0 \ end(vmatrix)$$

Visi šie skaitļi ir iegūti no Teilora sērijas, pieņemot, ka laika intervāls starp blakus esošajām novērotajām vērtībām ir nemainīgs un vienāds ar 1.

Tātad filtrēšanas problēma saskaņā ar mūsu izdarītajiem pieņēmumiem ir samazināta līdz parametru novērtēšanas problēmai; šajā gadījumā tiek novērtēti mūsu pieņemtā signāla ģenerēšanas modeļa parametri. Un stāvokļa vektora $X$ vērtību novērtējums tiek veikts, izmantojot to pašu formulu 3:

$$X_(ots)=(H^TH)^(-1)H^TZ$$

Būtībā mēs esam ieviesuši parametru novērtēšanas procesu, pamatojoties uz signāla ģenerēšanas procesa autoregresīvo modeli.

Formulu 3 var viegli ieviest programmatūrā, lai to izdarītu, ir jāaizpilda matrica $H$ un novērojumu kolonnas vektors $Z$. Tādus filtrus sauc filtri ar ierobežotu atmiņu, jo viņi izmanto pēdējos $k$ novērojumus, lai iegūtu pašreizējo novērtējumu $X_(noc)$. Katrā jaunā novērošanas solī esošajai novērojumu kopai tiek pievienots jauns un vecais tiek izmests. Šo aplēšu iegūšanas procesu sauc bīdāms logs.

Filtri ar augošu atmiņu

Filtriem ar ierobežotu atmiņu ir galvenais trūkums, ka pēc katra jauna novērojuma ir jāpārrēķina visi atmiņā saglabātie dati. Turklāt aplēšu aprēķināšanu var sākt tikai pēc tam, kad ir apkopoti pirmo $k$ novērojumu rezultāti. Tas nozīmē, ka šiem filtriem ir ilgs pārejas procesa ilgums.

Lai novērstu šo trūkumu, ir jāpāriet no filtra ar pastāvīgo atmiņu uz filtru ar augoša atmiņa. Šādā filtrā novēroto vērtību skaitam, pēc kura tiek veikts novērtējums, ir jāatbilst pašreizējā novērojuma skaitlim n. Tas ļauj iegūt aplēses, sākot no vairākiem novērojumiem, kas vienādi ar aprēķinātā vektora $X$ komponentu skaitu. Un to nosaka pieņemtā modeļa secība, tas ir, cik termini no Teilora sērijas tiek izmantoti modelī.

Šajā gadījumā, palielinoties n, uzlabojas filtra izlīdzināšanas īpašības, tas ir, palielinās aprēķinu precizitāte. Tomēr šīs pieejas tieša ieviešana ir saistīta ar skaitļošanas izmaksu pieaugumu. Tāpēc filtri ar pieaugošu atmiņu tiek ieviesti kā atkārtojas.

Fakts ir tāds, ka līdz laikam n mums jau ir aprēķins $X_((n-1)ots)$, kas satur informāciju par visiem iepriekšējiem novērojumiem $z_n, z_(n-1), z_(n-2) \dots z_ (n-(k-1))$. Aprēķins $X_(nots)$ tiek iegūts no nākamā novērojuma $z_n$, izmantojot aplēsē $X_((n-1))(\mbox (ots))$ saglabāto informāciju. Šo procedūru sauc par atkārtotu filtrēšanu, un tā sastāv no šādām darbībām:

• saskaņā ar aprēķinu $X_((n-1))(\mbox (ots))$, prognozējiet aprēķinu $X_n$, izmantojot formulu 4, ja $i = 1$: $X_(\mbox (notspriori)) = F_1X_( (n-1)ots)$. Šī ir a priori aplēse;
• saskaņā ar pašreizējā novērojuma $z_n$ rezultātiem šis a priori novērtējums tiek pārvērsts par patiesu, tas ir, a posteriori;
• šī procedūra tiek atkārtota katrā solī, sākot no $r+1$, kur $r$ ir filtra secība.

Galīgā atkārtotās filtrēšanas formula izskatās šādi:

$X_((n-1)oc) = X_(\mbox (nocapriori)) + (H^T_nH_n)^(-1)h^T_0(z_n - h_0 X_(\mbox (nocapriori)))$, (6 )

kur mūsu otrā pasūtījuma filtrs:

Pieaugošs atmiņas filtrs, kas darbojas saskaņā ar 6. formulu, ir īpašs filtrēšanas algoritma gadījums, kas pazīstams kā Kalmana filtrs.

Realizējot šo formulu praksē, jāatceras, ka tajā ietvertais apriori novērtējums tiek noteikts pēc formulas 4, un vērtība $h_0 X_(\mbox (nocapriori))$ apzīmē vektora $X_( pirmo komponentu. \mbox (nocapriori))$.

Pieaugošajam atmiņas filtram ir viena svarīga iezīme. Ja paskatās uz 6. formulu, galīgais novērtējums ir prognozētā novērtējuma vektora un korekcijas termiņa summa. Šī korekcija ir liela maziem $n$ un samazinās, palielinoties $n$, tiecoties līdz nullei pie $n \rightarrow \infty$. Tas ir, palielinoties n, palielinās filtra izlīdzināšanas īpašības un tajā iestrādātais modelis sāk dominēt. Bet reālais signāls modelim var atbilst tikai zināmā mērā. atsevišķas zonas, tāpēc prognozes precizitāte pasliktinās.

Lai to apkarotu, sākot no noteikta $n$, tiek noteikts aizliegums vēl vairāk samazināt korekcijas termiņu. Tas ir līdzvērtīgs filtra joslas maiņai, tas ir, maziem n filtrs ir plašāks joslas platums (mazāk inerciāls), lielam n tas kļūst inerciālāks.

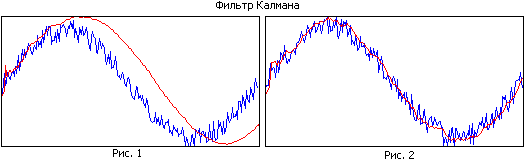
Salīdziniet 1. un 2. attēlu. Pirmajā attēlā filtram ir liela atmiņa, un tas labi izlīdzinās, taču šaurās joslas dēļ aprēķinātā trajektorija atpaliek no reālās. Otrajā attēlā filtra atmiņa ir mazāka, tas sliktāk izlīdzinās, bet labāk izseko reālo trajektoriju.

Literatūra

1. Ju.M. Koršunovs "Kibernētikas matemātiskie pamati"
2. A.V.Balakrišnans "Kalmana filtrācijas teorija"
3. V.N.Fomins "Atkārtota novērtēšana un adaptīvā filtrēšana"
4. C.F.N.Cowan, P.M. Piešķirt "Adaptīvos filtrus"

1. att

Tādējādi pāris, ko mēs meklējam, atrodas kaut kur uz šīs taisnes. Es atkārtoju, ka no visiem šiem variantiem nav iespējams izvēlēties pāri, kas faktiski eksistēja - kas deva skaitli 12, nezinot nekādus papildu pavedienus. tomēr situācijā, kurai tika izgudrots Kalmana filtrs, šādas norādes pastāv. Par nejaušiem skaitļiem ir kaut kas zināms jau iepriekš. Jo īpaši tur ir zināma tā sauktā sadalījuma histogramma katram skaitļu pārim. To parasti iegūst, pietiekami ilgi novērojot šo ļoti nejaušo skaitļu rašanos. Tas ir, piemēram, no pieredzes zināms, ka 5% gadījumu parasti parādās pāris x=1, y=8 (šo pāri apzīmējam šādi: (1,8)), 2% gadījumu pāris x=2, y=3 ( 2,3), 1% gadījumu pāris (3,1), 0,024% gadījumu pāris (11,1) utt. Es atkārtoju, šī histogramma ir dota visiem pāriem skaitļi, tostarp tie, kuru summa ir 12. Tādējādi katram pārim, kas saskaita līdz 12, varam teikt, ka, piemēram, pāris (1, 11) parādās 0,8% gadījumu, pāris ( 2, 10) – 1% gadījumu, pāris (3, 9) – 1,5% gadījumu utt. Tādējādi mēs varam izmantot histogrammu, lai noteiktu, cik procentos gadījumu pāra vārdu summa ir vienāda ar 12. Pieņemsim, piemēram, 30% gadījumu summa dod 12. Un atlikušajos 70% atlikušie pāri izkrīt - tie ir (1,8), (2, 3), (3,1) utt. – tie, kuru summa nav 12. Turklāt, lai, piemēram, pāris (7,5) parādās 27% gadījumu, bet visi pārējie pāri, kuru summa ir 12, parādās 0,024%+0,8% +1 %+1,5%+…=3% gadījumu. Tātad no histogrammas mēs noskaidrojām, ka skaitļi, kas kopā veido 12, parādās 30% gadījumu. Turklāt mēs zinām, ka, ja tiek izmests 12, tad visbiežāk (27% no 30%) iemesls tam ir pāris (7,5). Tas ir, ja jau Ja tiek izmests 12, mēs varam teikt, ka 90% gadījumu (27% no 30% - vai, kas ir tas pats, 27 reizes no katriem 30) 12 metiena iemesls ir pāris (7,5 ). Zinot, ka visbiežāk summas, kas vienāda ar 12, saņemšanas iemesls ir pāris (7,5), ir loģiski pieņemt, ka, visticamāk, tā šobrīd ir kritusies. Protams, joprojām nav fakts, ka faktiski tagad skaitli 12 veido tieši šis pāris, tomēr nākamreiz, ja sastapsimies ar 12 un atkal pieņemsim pāri (7,5), tad aptuveni 90% gadījumu no 100% mums būs taisnība. Bet, ja uzminēsim pāri (2, 10), mums būs taisnība tikai 1% no 30% gadījumu, kas ir vienāds ar 3,33% pareizo minējumu, salīdzinot ar 90%, uzminot pāri (7,5). Tā tas ir – tāda ir Kalmana filtra algoritma būtība. Tas ir, Kalmana filtrs negarantē, ka tas nekļūdīsies, nosakot summēšanu pēc summas, bet tas garantē, ka tas kļūdīsies minimālo reižu skaitu (kļūdas iespējamība būs minimāla), jo tajā tiek izmantota statistika – skaitļu pāru rašanās histogramma. Tāpat jāuzsver, ka Kalmana filtrēšanas algoritms bieži izmanto tā saukto varbūtības sadalījuma blīvumu (PDD). Tomēr ir jāsaprot, ka nozīme tur ir tāda pati kā histogrammai. Turklāt histogramma ir funkcija, kas izveidota, pamatojoties uz PDF, un ir tās tuvinājums (skatiet, piemēram,).
Principā mēs varam attēlot šo histogrammu kā divu mainīgo funkciju - tas ir, noteiktas virsmas formā virs xy plaknes. Kur virsma ir augstāka, varbūtība iegūt atbilstošo pāri ir lielāka. 2. attēlā parādīta šāda virsma.

2. att

Kā redzams virs taisnes x+y=12 (kurai ir došanas pāru varianti kopā 12), virsmas punkti atrodas dažādos augstumos un augstākais augstums ir variantam ar koordinātām (7,5). Un, kad mēs sastopamies ar summu, kas vienāda ar 12, 90% gadījumu šīs summas parādīšanās iemesls ir tieši pāris (7,5). Tie. Tieši šim pārim, kura summa ir 12, ir vislielākā rašanās varbūtība, ja summa ir 12.
Tādējādi Kalmana filtra ideja ir aprakstīta šeit. Uz šī pamata tiek veidotas visdažādākās tā modifikācijas - vienpakāpju, daudzpakāpju atkārtotas utt. Lai padziļināti izpētītu Kalmana filtru, es iesaku grāmatu: Van Trees G. Theory of Detection, estimation and modulation.

p.s. Tiem, kurus interesē matemātikas jēdzienu skaidrojumi, kā saka “uz pirkstiem”, mēs varam ieteikt šo grāmatu un jo īpaši tās sadaļas “Matemātika” nodaļas (var iegādāties gan pašu grāmatu, gan atsevišķas nodaļas no tās ).

Pētījums par Kalmana filtra izmantošanu integrētā mūsdienu attīstībā navigācijas sistēmas. Tiek sniegts un analizēts būvniecības piemērs matemātiskais modelis, kurā tiek izmantots paplašināts Kalmana filtrs, lai uzlabotu bezpilota lidaparātu koordinātu noteikšanas precizitāti. Tiek apsvērts daļējs filtrs. Izgatavots īss apskats zinātniskie darbi, izmantojot šo filtru, lai uzlabotu navigācijas sistēmu uzticamību un kļūdu toleranci. Šis raksts ļauj secināt, ka Kalmana filtra izmantošana UAV atrašanās vietas noteikšanas sistēmās tiek praktizēta daudzās mūsdienu izstrādēs. Šim lietojumam ir ļoti daudz variāciju un aspektu, kas arī sniedz taustāmus rezultātus, palielinot precizitāti, īpaši standarta satelītu navigācijas sistēmu atteices gadījumā. Tas ir galvenais faktors, kas ietekmē šīs tehnoloģijas dažādās zinātnes jomās, kas saistītas ar precīzu un defektu izturīgu navigācijas sistēmu izstrādi dažādiem gaisa kuģiem.

Kalmana filtrs

navigācija

bezpilota lidaparāts (UAV)

1. Makarenko G.K., Alešečkins A.M. Filtrēšanas algoritma izpēte, nosakot objekta koordinātas, izmantojot signālus no satelīta radionavigācijas sistēmām // TUSUR ziņojumi. – 2012. – Nr.2 (26). – 15.-18.lpp.

2. Bar-Shalom Y., Li X. R., Kirubarajan T. Estimation with Applications

uz izsekošanu un navigāciju // Teorijas algoritmi un programmatūra. – 2001. – Sēj. 3. – 10.-20.lpp.

3. Bassem I.S. Uz redzi balstīta bezpilota lidaparātu (UAV) navigācija (VBN) // KALGARIJAS UNIVERSITĀTE. – 2012. – sēj. 1. – P. 100-127.

4. Conte G., Doherty P. Integrēta UAV navigācijas sistēma, kuras pamatā ir aeroattēlu saskaņošana // Aerospace Conference. – 2008. –Sēj. 1. – P. 3142-3151.

5. Guoqiang M., Drake S., Anderson B. Design of an extension Kalman filter for uav localization // In Information, Decision and Control. – 2007. – Sēj. 7. – 224.–229.lpp.

6. Ponda S.S trajektorijas optimizācija mērķa lokalizācijai, izmantojot mazus bezpilota gaisa transportlīdzekļus // Masačūsetsas Tehnoloģiju institūts. – 2008. – Sēj. 1. – 64.-70.lpp.

7. Wang J., Garrat M., Lambert A. Integration of GPS/ins/vision sensors to navigation bezpilota lidaparātos // IAPRS&SIS. – 2008. – Sēj. 37. – P. 963-969.

Viens no neatliekamajiem bezpilota lidaparātu (UAV) mūsdienu navigācijas uzdevumiem ir uzdevums palielināt koordinātu noteikšanas precizitāti. Šī problēma tiek atrisināta, izmantojot dažādas navigācijas sistēmu integrācijas iespējas. Viena no modernajām integrācijas iespējām ir GPS/GLONASS navigācijas kombinācija ar paplašināto Kalmanfiltru, kas rekursīvi novērtē precizitāti, izmantojot nepilnīgus un trokšņainus mērījumus. Šobrīd pastāv un tiek izstrādātas dažādas paplašinātā Kalmana filtra variācijas, tostarp daudzveidīgs skaits stāvokļa mainīgo. Šajā darbā mēs parādīsim, cik efektīva var būt tā izmantošana mūsdienu attīstībā. Apskatīsim vienu no šāda filtra raksturīgajiem attēlojumiem.

Matemātiskā modeļa veidošana

IN šajā piemērā mēs runāsim tikai par UAV kustību horizontālajā plaknē, pretējā gadījumā mēs apsvērsim tā saukto 2d lokalizācijas problēmu. Mūsu gadījumā tas ir attaisnojams ar to, ka daudzās praktiski sastopamās situācijās UAV var palikt aptuveni tādā pašā augstumā. Šis pieņēmums tiek plaši izmantots, lai vienkāršotu gaisa kuģu dinamikas simulācijas. UAV dinamisko modeli nosaka šāda vienādojumu sistēma:

kur () ir bezpilota lidaparāta koordinātas horizontālajā plaknē kā laika funkcija, UAV virziens, UAV leņķiskais ātrums un bezpilota lidaparāta kustības ātrums, un tās tiks uzskatītas par nemainīgām. Tie ir savstarpēji neatkarīgi, ar zināmām kovariācijām un , ir vienāds ar un attiecīgi, un tiek izmantotas, lai modelētu vēja, pilota manevru u.c. izraisītas UAV paātrinājuma izmaiņas. Vērtības un ir iegūtas no UAV maksimālā leņķiskā ātruma un UAV lineārā ātruma izmaiņu eksperimentālajām vērtībām - Kronecker simbols.

Šī vienādojumu sistēma būs aptuvena modeļa nelinearitātes un trokšņa klātbūtnes dēļ. Vienkāršākā tuvināšanas metode šajā gadījumā ir Eilera aproksimācijas metode. Tālāk ir parādīts UAV dinamiskās piedziņas sistēmas diskrēts modelis.

diskrēts Kalmana filtra stāvokļa vektors, kas ļauj tuvināt nepārtraukta stāvokļa vektora vērtību. ∆ - laika intervāls starp k un k+1 mērījumiem. () un () ir baltā Gausa trokšņa vērtību secības ar nulles vidējo vērtību. Kovariācijas matrica pirmajai secībai:

Līdzīgi otrajai secībai:

Veicot atbilstošās aizstāšanas sistēmas (2) vienādojumos, mēs iegūstam:

Secības un ir savstarpēji neatkarīgas. Tās ir arī nulles vidējā baltā Gausa trokšņa sekvences ar kovariācijas matricām un attiecīgi. Šīs formas priekšrocība ir tā, ka tā parāda diskrētā trokšņa izmaiņas starp katru mērījumu. Rezultātā mēs iegūstam šādu diskrēto dinamisko modeli:

(3)

Vienādojums:

= + , (4)

kur x un y ir bezpilota lidaparāta koordinātas k laika momentā un nejaušu parametru Gausa secība ar nulles vidējo vērtību, ko izmanto kļūdas iestatīšanai. Tiek pieņemts, ka šī secība ir neatkarīga no () un ().

Izteiksmes (3) un (4) kalpo par pamatu UAV atrašanās vietas noteikšanai, kur k-e koordinātas iegūts, izmantojot paplašināto Kalman filtru. Navigācijas sistēmu modelēšanas kļūme saistībā ar šis tips filtrs parāda tā ievērojamo efektivitāti.

Lai iegūtu lielāku skaidrību, sniegsim nelielu vienkāršu piemēru. Ļaujiet dažiem bezpilota lidaparātiem lidot vienmērīgi paātrināti ar nemainīgu paātrinājumu a.

Kur x ir UAV koordināte laikā t, un δ ir kāds nejaušs mainīgais.

Pieņemsim, ka mums ir GPS sensors, kas saņem datus par lidmašīnas atrašanās vietu. Iesniegsim šī procesa modelēšanas rezultātu MATLAB programmatūras pakotnē.

Rīsi. 1. Sensoru rādījumu filtrēšana, izmantojot Kalmana filtru

Attēlā 1 parāda, cik efektīva var būt Kalmana filtrēšanas izmantošana.

Tomēr reālās situācijās signāliem bieži ir nelineāra dinamika un neparasti trokšņi. Šādos gadījumos tiek izmantots paplašinātais Kalman filtrs. Ja trokšņu atšķirības nav pārāk lielas (t.i., lineārā tuvināšana ir piemērota), paplašinātā Kalmana filtra izmantošana nodrošina problēmas risinājumu ar augstu precizitāti. Tomēr gadījumā, ja troksnis nav Gausa troksnis, paplašināto Kalmana filtru nevar izmantot. Šajā gadījumā parasti tiek izmantots daļējs filtrs, kurā tiek izmantotas skaitliskās integrālās metodes, kuru pamatā ir Montekarlo metodes ar Markova ķēdēm.

Daļējs filtrs

Iedomāsimies vienu no algoritmiem, kas attīsta paplašinātā Kalmana filtra idejas – daļējo filtru. Daļēja filtrēšana ir neoptimāls filtrēšanas paņēmiens, kas darbojas, veicot Montekarlo apvienošanu daļiņu kopai, kas atspoguļo procesa varbūtības sadalījumu. Šeit daļiņa ir elements, kas ņemts no novērtējamā parametra iepriekšējā sadalījuma. Daļēja filtra pamatideja ir tāda, ka lielu daļiņu skaitu var izmantot, lai attēlotu sadalījuma novērtējumu. Jo lielāks ir izmantoto daļiņu skaits, jo precīzāk daļiņu kopa attēlos iepriekšējo sadalījumu. Daļiņu filtrs tiek inicializēts, ievietojot tajā N daļiņas no iepriekšēja to parametru sadalījuma, kurus vēlamies novērtēt. Filtrēšanas algoritms ietver šo daļiņu izlaišanu cauri īpaša sistēma, un pēc tam nosverot, izmantojot informāciju, kas iegūta, mērot šīs daļiņas. Iegūtās daļiņas un ar tām saistītās masas atspoguļo aplēses procesa aizmugurējo sadalījumu. Ciklu atkārto katram jaunam mērījumam, un daļiņu svars tiek atjaunināts, lai attēlotu turpmāko sadalījumu. Viena no galvenajām problēmām ar tradicionālo daļiņu filtrēšanas pieeju ir tā, ka šīs pieejas rezultātā dažām daļiņām ir ļoti liels svars, pretstatā lielākajai daļai citu daļiņu ir ļoti mazs svars. Tas noved pie filtrēšanas nestabilitātes. Šo problēmu var atrisināt, ieviešot paraugu ņemšanas ātrumu, kurā N jaunas daļiņas tiek ņemtas no sadalījuma, kas sastāv no vecajām daļiņām. Novērtējuma rezultātu iegūst, ņemot daļiņu kopas vidējās vērtības paraugu. Ja mums ir vairāki neatkarīgi paraugi, izlases vidējais rādītājs būs precīzs vidējās vērtības novērtējums, norādot galīgo dispersiju.

Pat ja daļiņu filtrs ir suboptimāls, tad, tā kā daļiņu skaitam ir tendence uz bezgalību, algoritma efektivitāte tuvojas Bajesa novērtējuma likumam. Tāpēc ir vēlams iegūt pēc iespējas vairāk daļiņu labākais rezultāts. Diemžēl tas ievērojami palielina aprēķinu sarežģītību un līdz ar to liek kompromisam starp precizitāti un aprēķinu ātrumu. Tātad daļiņu skaits jāizvēlas, pamatojoties uz precizitātes novērtējuma uzdevuma prasībām. Vēl viens svarīgs faktors daļiņu filtra darbībā ir paraugu ņemšanas ātruma ierobežojums. Kā minēts iepriekš, paraugu ņemšanas ātrums ir svarīgs parametrs daļiņu filtrēšanai, un bez tā algoritms galu galā kļūs deģenerēts. Ideja ir tāda, ka, ja svari ir sadalīti pārāk nevienmērīgi un drīz tiks sasniegts paraugu ņemšanas slieksnis, mazsvara daļiņas tiek izmestas un atlikušais kopums veido jaunu varbūtības blīvumu, no kura var ņemt jaunus paraugus. Iztveršanas ātruma sliekšņa izvēle ir diezgan grūts uzdevums, jo arī augsta frekvence izraisa filtru pārāk jutīgu pret troksni, un pārāk zems rada lielu kļūdu. Svarīgs faktors ir arī varbūtības blīvums.

Kopumā daļiņu filtrēšanas algoritms parāda labu pozīcijas aprēķināšanas veiktspēju stacionāriem mērķiem un salīdzinoši lēni kustīgu mērķu gadījumā ar nezināmu paātrinājuma dinamiku. Kopumā daļiņu filtrēšanas algoritms ir stabilāks nekā paplašinātais Kalmana filtrs un mazāk pakļauts deģenerācijai un nopietnām kļūmēm. Nelineāra, ne Gausa sadalījuma gadījumos šis algoritms filtrēšana parāda ļoti labu precizitāti mērķa atrašanās vietas noteikšanā, savukārt paplašināto Kalmana filtrēšanas algoritmu šādos apstākļos nevar izmantot. Šīs pieejas trūkumi ietver tās augstāko sarežģītību salīdzinājumā ar paplašināto Kalmana filtru, kā arī to, ka ne vienmēr ir skaidrs, kā izvēlēties pareizos parametrus šim algoritmam.

Daudzsološi pētījumi šajā jomā

Mūsu piedāvātajam līdzīga Kalmana filtra modeļa izmantošana ir redzama, kur tas tiek izmantots integrētas sistēmas veiktspējas uzlabošanai (GPS + datorredzes modelis saskaņošanai ar ģeogrāfisko bāzi), un situācija tiek simulēta arī satelītnavigācijas iekārtu atteice. Izmantojot Kalmana filtru, tika ievērojami uzlaboti sistēmas rezultāti atteices gadījumā (piemēram, kļūda augstuma noteikšanā tika samazināta aptuveni divas reizes, un kļūdas, nosakot koordinātas pa dažādām asīm, tika samazinātas gandrīz 9 reizes) . Ir norādīts arī līdzīgs Kalmana filtra lietojums.

Interesanta problēma no metožu kopuma viedokļa ir atrisināta . Tas izmanto arī 5 stāvokļu Kalman filtru ar dažām atšķirībām modeļa konstrukcijā. Iegūtais rezultāts pārsniedz mūsu prezentētā modeļa rezultātu, jo tiek izmantoti papildu integrācijas līdzekļi (tiek izmantoti fotoattēli un termoattēlveidošanas attēli). Kalmana filtra izmantošana šajā gadījumā ļauj samazināt kļūdu, nosakot dotā punkta telpiskās koordinātas, līdz vērtībai 5,5 m.

Secinājums

Noslēgumā mēs atzīmējam, ka Kalmana filtra izmantošana UAV atrašanās vietas noteikšanas sistēmās tiek praktizēta daudzās mūsdienu izstrādēs. Šim lietojumam ir ļoti daudz variāciju un aspektu, līdz pat vairāku līdzīgu filtru vienlaicīgai lietošanai ar dažādiem stāvokļa faktoriem. Viens no perspektīvākajiem Kalmana filtru izstrādes virzieniem šķiet modificēta filtra izveide, kura kļūdas attēlos krāsains troksnis, kas padarīs to vēl vērtīgāku reālu problēmu risināšanai. Lielu interesi šajā jomā rada arī daļējs filtrs, kas var filtrēt ne Gausa troksni. Šī daudzveidība un taustāmie rezultāti precizitātes uzlabošanā, īpaši standarta satelītnavigācijas sistēmu atteices gadījumā, ir galvenie faktori šīs tehnoloģijas ietekmei uz dažādām zinātnes jomām, kas saistītas ar precīzu un defektiem izturīgu navigācijas sistēmu izstrādi dažādiem gaisa kuģiem. .

Recenzenti:

Labunets V.G., tehnisko zinātņu doktors, profesors, katedras profesors teorētiskie pamati Urālu federālās universitātes radiotehnika, kas nosaukta pirmā Krievijas prezidenta B.N. vārdā. Jeļcins, Jekaterinburga;

Ivanovs V.E., tehnisko zinātņu doktors, profesors, vadītājs. Urālu federālās universitātes Tehnoloģiju un komunikāciju katedra nosaukta pirmā Krievijas prezidenta B.N. Jeļcins, Jekaterinburga.

Bibliogrāfiskā saite

Random Forest ir viens no maniem iecienītākajiem datu ieguves algoritmiem. Pirmkārt, tas ir neticami daudzpusīgs, to var izmantot gan regresijas, gan klasifikācijas problēmu risināšanai. Meklējiet anomālijas un atlasiet prognozētājus. Otrkārt, šis ir algoritms, kuru ir patiešām grūti nepareizi piemērot. Vienkārši tāpēc, ka atšķirībā no citiem algoritmiem tam ir maz pielāgojamu parametru. Un arī pēc būtības tas ir pārsteidzoši vienkāršs. Un tajā pašā laikā tas ir pārsteidzoši precīzs.

Kāda ir šāda brīnišķīga algoritma ideja? Ideja ir vienkārša: pieņemsim, ka mums ir kāds ļoti vājš algoritms, teiksim . Ja mēs izveidosim daudz dažādu modeļu, izmantojot šo vājo algoritmu un aprēķināsim to prognožu rezultātus, gala rezultāts būs ievērojami labāks. To sauc par ansambļa mācīšanos darbībā. Tāpēc Random Forest algoritmu sauc par “Random Forest”; saņemtajiem datiem tas izveido daudzus lēmumu kokus un pēc tam nosaka to prognožu rezultātu vidējo vērtību. Svarīgs punkts šeit ir nejaušības elements katra koka izveidē. Galu galā ir skaidrs, ka, ja mēs izveidosim daudzus identiskus kokus, tad to vidējā noteikšanas rezultāts būs viena koka precizitāte.

Kā viņš strādā? Pieņemsim, ka mums ir daži ievades dati. Katra kolonna atbilst kādam parametram, katra rinda atbilst kādam datu elementam.

Mēs varam nejauši atlasīt noteiktu skaitu kolonnu un rindu no visas datu kopas un, pamatojoties uz tiem, izveidot lēmumu koku.

Ceturtdiena, 2012. gada 10. maijs

Ceturtdiena, 2012. gada 12. janvāris

Tas viss sākās 2011. gada aprīlī, kad man bija telefona intervija ar Zynga. Tad tas viss likās kā kaut kāda ar realitāti nesaistīta spēle un es pat nevarēju iedomāties, pie kā tas novedīs. 2011. gada jūnijā Zynga ieradās Maskavā un veica virkni interviju, tika izskatīti aptuveni 60 kandidāti, kuri izturēja telefona interviju un no tiem tika atlasīti aptuveni 15 cilvēki (nezinu precīzu skaitu, daži vēlāk pārdomāja, citi nekavējoties atteicās). Intervija izrādījās pārsteidzoši vienkārša. Nav programmēšanas problēmu, nav sarežģītu jautājumu par lūku formu, galvenokārt pārbaudot jūsu spēju tērzēt. Un zināšanas, manuprāt, tika vērtētas tikai virspusēji.

Un tad sākās strīds. Vispirms gaidījām rezultātus, tad piedāvājumu, tad LCA apstiprinājumu, tad vīzas petīcijas apstiprināšanu, tad dokumentus no ASV, tad rindu pie vēstniecības, tad papildus pārbaudi, tad vīzu. Brīžiem man šķita, ka esmu gatava atdot visu un gūt vārtus. Brīžiem šaubījos, vai mums vajag šo Ameriku, galu galā arī Krievija nav slikta. Viss process ilga apmēram pusgadu, beigās decembra vidū saņēmām vīzas un sākām gatavoties izbraukšanai.

Pirmdiena bija mana pirmā darba diena jaunā vietā. Birojā ir visi apstākļi ne tikai strādāt, bet arī dzīvot. Brokastis, pusdienas un vakariņas mūsu pašu šefpavāri, daudz un daudzveidīgs ēdiens, kas sabāzts katrā stūrī, trenažieru zāle, masāža un pat frizieris. Tas viss darbiniekiem ir pilnīgi bez maksas. Daudzi cilvēki uz darbu brauc ar velosipēdu, vairākas telpas ir aprīkotas transportlīdzekļu glabāšanai. Vispār neko tādu Krievijā neesmu redzējis. Tomēr visam ir sava cena, mūs uzreiz brīdināja, ka būs daudz jāstrādā. Kas pēc viņu standartiem ir “daudz”, man nav īsti skaidrs.

Ceru tomēr, ka, neskatoties uz darba apjomu, pārskatāmā nākotnē varēšu atsākt blogošanu un, iespējams, pastāstīt kaut ko par amerikāņu dzīvi un programmētāja darbu Amerikā. Gaidi un redzēsi. Tikmēr novēlu visiem laimīgu Jauno gadu un Ziemassvētkus un tiekamies atkal!

Rezultāts<- NULL for(i in (1:length(divs[,1]))){ d <- divs if (d$Divs>0)( try(( pēdiņas<- getSymbols(d$Symbol, src="Finam", from="2010-01-01", auto.assign=FALSE) if (!is.nan(quotes)){ price <- Cl(quotes) if (length(price)>0)(dd<- d$Divs result <- rbind(result, data.frame(d$Symbol, d$Name, d$RegistryDate, as.numeric(dd)/as.numeric(price), stringsAsFactors=FALSE)) } } }, silent=TRUE) } } colnames(result) <- c("Symbol", "Name", "RegistryDate", "Divs") result

Internetā, tostarp vietnē Habré, varat atrast daudz informācijas par Kalmana filtru. Bet pašām formulām ir grūti atrast viegli sagremojamu secinājumu. Bez slēdziena visa šī zinātne tiek uztverta kā sava veida šamanisms, formulas izskatās kā bezsejas simbolu kopums, un pats galvenais, daudzi vienkārši apgalvojumi, kas guļ uz teorijas virsmas, ir nesaprotami. Šī raksta mērķis būs runāt par šo filtru pēc iespējas pieejamākā valodā.
Kalmana filtrs ir spēcīgs datu filtrēšanas rīks. Tās galvenais princips ir tāds, ka filtrēšanai tiek izmantota informācija par pašas parādības fiziku. Teiksim, ja filtrē datus no automašīnas spidometra, tad mašīnas inerce dod tiesības uztvert pārāk ātrus ātruma lēcienus kā mērījuma kļūdu. Kalmana filtrs ir interesants, jo savā ziņā tas ir labākais filtrs. Tālāk mēs sīkāk apspriedīsim, ko īsti nozīmē vārdi “labākais”. Raksta beigās parādīšu, ka daudzos gadījumos formulas var vienkāršot tiktāl, ka no tām gandrīz nekas nepaliek.

Izglītības programma

Pirms iepazīšanās ar Kalmana filtru iesaku atgādināt dažas vienkāršas definīcijas un faktus no varbūtību teorijas.

Izlases vērtība

Kad viņi saka, ka ir dots nejaušs mainīgais, viņi nozīmē, ka šai vērtībai var būt nejaušas vērtības. Tas iegūst dažādas vērtības ar dažādām varbūtībām. Kad metīsit, teiksim, kauliņu, parādīsies diskrēts vērtību kopums: . Ja mēs runājam, piemēram, par klejojošas daļiņas ātrumu, tad acīmredzot mums ir jārisina nepārtraukta vērtību kopa. Mēs apzīmēsim nejaušā mainīgā “izkritušās” vērtības, izmantojot , bet dažreiz mēs izmantosim to pašu burtu, ar kuru mēs apzīmējam nejaušo mainīgo: .
Nepārtrauktas vērtību kopas gadījumā gadījuma lielumu raksturo varbūtības blīvums, kas mums nosaka, ka varbūtība, ka gadījuma lielums “izkritīs” nelielā garuma punkta apkārtnē, ir vienāda ar . Kā redzams no attēla, šī varbūtība ir vienāda ar ēnotā taisnstūra laukumu zem diagrammas:

Diezgan bieži dzīvē nejaušie mainīgie ir Gausa sadalīti, ja varbūtības blīvums ir vienāds ar .

Mēs redzam, ka funkcijai ir zvana forma ar centru vienā punktā un raksturīgu secības platumu.
Tā kā mēs runājam par Gausa sadalījumu, būtu kauns nepieminēt, no kurienes tas nāk. Tāpat kā skaitļi ir stingri nostiprinājušies matemātikā un ir atrodami visnegaidītākajās vietās, arī Gausa sadalījums ir ieņēmis dziļas saknes varbūtību teorijā. Viens ievērojams apgalvojums, kas daļēji izskaidro Gausa visuresamību, ir šāds:
Lai ir nejaušs mainīgais ar patvaļīgu sadalījumu (patiesībā šai patvaļai ir daži ierobežojumi, taču tie nebūt nav stingri). Veiksim eksperimentus un aprēķināsim nejauša lieluma “izkritušo” vērtību summu. Veiksim daudzus šādus eksperimentus. Skaidrs, ka katru reizi saņemsim citu summas vērtību. Citiem vārdiem sakot, šī summa pati par sevi ir nejaušs lielums ar savu specifisko sadalījuma likumu. Izrādās, ka, esot pietiekami lielam, šīs summas sadalījuma likums tiecas uz Gausa sadalījumu (starp citu, “zvaniņam” raksturīgais platums pieaug par ). Sīkāk mēs lasām Vikipēdijā: centrālās robežas teorēma. Dzīvē ļoti bieži ir daudzumi, kas ir liela skaita identiski sadalītu neatkarīgu gadījuma lielumu summa, un tāpēc tie ir Gausa sadalīti.

Vidējā vērtība

Gadījuma lieluma vidējā vērtība ir tā, ko mēs iegūsim robežās, ja veiksim daudz eksperimentu un aprēķināsim kritušo vērtību vidējo aritmētisko. Vidējā vērtība tiek apzīmēta dažādos veidos: matemātiķiem patīk to apzīmēt caur (matemātiskā cerība), bet ārzemju matemātiķiem - caur (cerība). Fiziķi caur vai. Mēs to apzīmēsim svešā veidā: .
Piemēram, Gausa sadalījumam vidējais ir .

Izkliede

Gausa sadalījuma gadījumā mēs skaidri redzam, ka nejaušais mainīgais dod priekšroku krist noteiktā apkārtnē no tā vidējās vērtības. Kā redzams no grafika, raksturīgā vērtību izplatība ir . Kā mēs varam novērtēt šo vērtību izplatību patvaļīgam gadījuma mainīgajam, ja mēs zinām tā sadalījumu? Varat uzzīmēt tā varbūtības blīvuma grafiku un ar aci novērtēt raksturīgo platumu. Bet mēs dodam priekšroku algebriskajam ceļam. Jūs varat atrast vidējo novirzes garumu (moduli) no vidējās vērtības: . Šī vērtība būs labs vērtību raksturīgās izplatības novērtējums. Bet jūs un es ļoti labi zinām, ka moduļu izmantošana formulās ir galvassāpes, tāpēc šī formula tiek reti izmantota, lai novērtētu raksturīgo izkliedi.
Vienkāršāks veids (vienkāršs aprēķinu ziņā) ir atrast . Šo daudzumu sauc par dispersiju, un to bieži apzīmē kā . Dispersijas sakni sauc par standarta novirzi. Standarta novirze ir labs nejaušā mainīgā lieluma izplatības novērtējums.
Piemēram, Gausa sadalījumam mēs varam aprēķināt, ka iepriekš definētā dispersija ir precīzi vienāda ar , kas nozīmē, ka standarta novirze ir vienāda ar , kas ļoti labi saskan ar mūsu ģeometrisko intuīciju.
Patiesībā šeit ir paslēpta neliela krāpniecība. Fakts ir tāds, ka Gausa sadalījuma definīcijā zem eksponenta ir izteiksme. Šie divi ir saucējā tieši tāpēc, lai standartnovirze būtu vienāda ar koeficientu. Tas ir, pati Gausa sadalījuma formula ir uzrakstīta formā, kas ir īpaši pielāgota, lai mēs aprēķinātu tās standarta novirzi.

Neatkarīgi nejauši mainīgie

Nejaušie mainīgie var būt atkarīgi vai ne. Iedomājieties, ka iemet adatu plaknē un ieraksta abu galu koordinātas. Šīs divas koordinātas ir atkarīgas; tās ir saistītas ar nosacījumu, ka attālums starp tām vienmēr ir vienāds ar adatas garumu, lai gan tie ir nejauši mainīgie.
Gadījuma mainīgie ir neatkarīgi, ja pirmā rezultāts ir pilnīgi neatkarīgs no otrā rezultāta. Ja nejaušie mainīgie ir neatkarīgi, tad to reizinājuma vidējā vērtība ir vienāda ar to vidējo vērtību reizinājumu:

Pierādījums

Piemēram, zilas acis un skolas beigšana ar zelta medaļu ir neatkarīgi nejauši mainīgie. Ja zilacaini, teiksim, zelta medaļnieki, tad zilacainie. Šis piemērs parāda, ka, ja gadījuma lielumus nosaka pēc to varbūtības blīvuma un , tad šo vērtību neatkarība izpaužas ar to, ka varbūtības blīvums ( pirmā vērtība izkrita, bet otrā) tiek atrasta pēc formulas:

No tā uzreiz izriet, ka:

Kā redzat, pierādījums tika veikts nejaušiem mainīgajiem, kuriem ir nepārtraukts vērtību spektrs un kurus nosaka to varbūtības blīvums. Citos gadījumos pierādījumu ideja ir līdzīga.

Kalmana filtrs

Problēmas formulēšana

Apzīmēsim vērtību, kuru mērīsim un pēc tam filtrēsim. Tas varētu būt stāvoklis, ātrums, paātrinājums, mitrums, smakas pakāpe, temperatūra, spiediens utt.
Sāksim ar vienkāršu piemēru, kas novedīs pie vispārējās problēmas formulējuma. Iedomājieties, ka mums ir radiovadāma automašīna, kas var braukt tikai uz priekšu un atpakaļ. Mēs, zinot automašīnas svaru, formu, ceļa segumu utt., aprēķinājām, kā vadības kursorsvira ietekmē kustības ātrumu.

Tad automašīnas koordinātas mainīsies saskaņā ar likumu:

Reālajā dzīvē mēs nevaram savos aprēķinos ņemt vērā nelielus traucējumus, kas iedarbojas uz automašīnu (vējš, nelīdzenumi, oļi uz ceļa), tāpēc reālais automašīnas ātrums atšķirsies no aprēķinātā. Ierakstītā vienādojuma labajā pusē tiks pievienots nejaušs mainīgais:

Mums automašīnai ir uzstādīts GPS sensors, kas mēģina izmērīt automašīnas patieso koordinātu, un, protams, nevar to precīzi izmērīt, bet mēra ar kļūdu, kas arī ir nejaušs lielums. Rezultātā mēs saņemam kļūdainus datus no sensora:

Uzdevums ir, zinot nepareizos sensora rādījumus, atrast labu aptuvenu automašīnas patieso koordinātu.
Vispārīgās problēmas formulējumā par koordinātu var būt atbildīgs jebkas (temperatūra, mitrums...), un par sistēmas vadību no ārpuses atbildīgo dalībnieku apzīmēsim kā (piemērā ar mašīnu). Koordinātu un sensoru rādījumu vienādojumi izskatīsies šādi:

Sīkāk apspriedīsim to, ko mēs zinām:

Ir vērts atzīmēt, ka filtrēšanas uzdevums nav izlīdzināšanas uzdevums. Mēs necenšamies izlīdzināt sensora datus, mēs cenšamies iegūt vistuvāko vērtību reālajai koordinātei.

Kalmana algoritms

Mēs strīdēsimies ar indukciju. Iedomājieties, ka solī mēs jau esam atraduši sensora filtrētu vērtību, kas labi tuvina sistēmas patieso koordinātu. Neaizmirstiet, ka mēs zinām vienādojumu, kas kontrolē nezināmās koordinātas izmaiņas:

Tāpēc, vēl nesaņemot vērtību no sensora, mēs varam pieņemt, ka solī sistēma attīstīsies saskaņā ar šo likumu un sensors parādīs kaut ko tuvu . Diemžēl pagaidām neko precīzāku pateikt nevaram. No otras puses, soļa laikā mūsu rokās būs neprecīzs sensora rādījums.
Kalmana ideja ir šāda. Lai iegūtu vislabāko tuvinājumu patiesajai koordinātei, mums ir jāizvēlas vidusceļš starp neprecīzo sensora nolasījumu un mūsu prognozi par to, ko mēs gaidījām. Sensora rādījumam piešķirsim svaru, un svars paliks uz prognozētās vērtības:

Koeficientu sauc par Kalmana koeficientu. Tas ir atkarīgs no iterācijas soļa, tāpēc pareizāk būtu rakstīt , bet pagaidām, lai nepārblīvētu aprēķina formulas, tā indeksu izlaidīsim.
Mums jāizvēlas Kalmana koeficients, lai iegūtā optimālā koordinātu vērtība būtu vistuvāk patiesajai. Piemēram, ja zinām, ka mūsu sensors ir ļoti precīzs, tad vairāk uzticēsimies tā rādījumam un piešķirsim vērtībai lielāku svaru (tuvu vienam). Ja sensors, gluži pretēji, nav precīzs, tad mēs vairāk koncentrēsimies uz teorētiski prognozēto vērtību.
Kopumā, lai atrastu precīzu Kalmana koeficienta vērtību, jums vienkārši jāsamazina kļūda:

Mēs izmantojam vienādojumus (1) (tie, kas atrodas kadrā zilajā fonā), lai pārrakstītu kļūdas izteiksmi:

Pierādījums

Tagad ir pienācis laiks apspriest, ko nozīmē izteiciens samazināt kļūdu? Galu galā kļūda, kā mēs redzam, pati par sevi ir nejaušs mainīgais un katru reizi iegūst dažādas vērtības. Patiesībā nav nevienas universālas pieejas, lai definētu, ko nozīmē minimāla kļūda. Tāpat kā gadījuma lieluma dispersijas gadījumā, kad mēģinājām novērtēt tā dispersijas raksturīgo platumu, arī šeit aprēķiniem izvēlēsimies vienkāršāko kritēriju. Mēs samazināsim kvadrātiskās kļūdas vidējo vērtību:

Pierakstīsim pēdējo izteiksmi:

Pierādījums

No tā, ka visi izteiksmē iekļautie nejaušie mainīgie ir neatkarīgi, izriet, ka visi “krustveida” vārdi ir vienādi ar nulli:

Mēs izmantojām faktu, ka , tad dispersijas formula izskatās daudz vienkāršāka: .

Šī izteiksme iegūst minimālo vērtību, ja (atvasinājumu pielīdzinām nullei):

Šeit mēs jau rakstām izteiksmi Kalmana koeficientam ar soļu indeksu, tādējādi uzsverot, ka tas ir atkarīgs no iterācijas soļa.
Mēs aizstājam iegūto optimālo vērtību izteiksmē , kuru mēs samazinājām. Mēs saņemam;

Mūsu problēma ir atrisināta. Esam ieguvuši iteratīvu formulu Kalmana koeficienta aprēķināšanai.
Apkoposim mūsu iegūtās zināšanas vienā rāmī:

Piemērs

Matlab kods

Iztīrīt visu; N=100% paraugu skaits a=0,1% paātrinājums sigmaPsi=1 sigmaEta=50; k=1:N x=k x(1)=0 z(1)=x(1)+normrnd(0,sigmaEta); ja t=1:(N-1) x(t+1)=x(t)+a*t+normrnd(0,sigmaPsi); z(t+1)=x(t+1)+normrnd(0,sigmaEta); beigas; %kalman filtrs xOpt(1)=z(1); eOpt(1)=sigmaEta; ja t=1:(N-1) eOpt(t+1)=sqrt((sigmaEta^2)*(eOpt(t)^2+sigmaPsi^2)/(sigmaEta^2+eOpt(t)^2+ sigmaPsi^2)) K(t+1)=(eOpt(t+1))^2/sigmaEta^2 xOpt(t+1)=(xOpt(t)+a*t)*(1-K(t) +1))+K(t+1)*z(t+1) beigas; plot(k,xOpt,k,z,k,x)

Analīze

Ja izsekojat, kā Kalmana koeficients mainās ar iterācijas soļiem, varat parādīt, ka tas vienmēr stabilizējas līdz noteiktai vērtībai. Piemēram, ja sensora un modeļa vidējo kvadrātisko kļūdu attiecība ir desmit pret vienu, tad Kalmana koeficienta grafiks atkarībā no iterācijas soļa izskatās šādi:

Nākamajā piemērā mēs apspriedīsim, kā tas var ievērojami atvieglot mūsu dzīvi.

Otrais piemērs

Praksē bieži gadās, ka mēs vispār neko nezinām par filtrējamā fizisko modeli. Piemēram, jūs vēlējāties filtrēt rādījumus no sava iecienītākā akselerometra. Jūs iepriekš nezināt, ar kādu likumu jūs plānojat pagriezt akselerometru. Lielākā daļa informācijas, ko varat iegūt, ir sensora kļūdu dispersija. Šādā sarežģītā situācijā visa kustības modeļa nezināšana var tikt novirzīta nejaušā mainīgā:

Bet, atklāti sakot, šāda sistēma vairs neatbilst nosacījumiem, ko mēs uzlikām nejaušajam mainīgajam, jo ​​tagad visa nezināmā kustības fizika ir tur paslēpta, un tāpēc nevar teikt, ka dažādos laika momentos modeļa kļūdas ir neatkarīgas no viens otru un ka to vidējās vērtības ir nulle. Šajā gadījumā kopumā Kalmana filtra teorija nav piemērojama. Bet mēs šim faktam nepievērsīsim uzmanību, bet stulbi pielietosim visu formulu kolosu, izvēloties koeficientus pēc acs, lai filtrētie dati izskatās jauki.
Bet jūs varat izvēlēties citu, daudz vienkāršāku ceļu. Kā redzējām iepriekš, Kalmana koeficients vienmēr stabilizējas līdz vērtībai, kad tas palielinās. Tāpēc tā vietā, lai atlasītu koeficientus un atrastu Kalmana koeficientu, izmantojot sarežģītas formulas, mēs varam uzskatīt, ka šis koeficients vienmēr ir konstante, un izvēlēties tikai šo konstanti. Šis pieņēmums gandrīz neko nesabojās. Pirmkārt, mēs jau nelegāli izmantojam Kalmana teoriju, otrkārt, Kalmana koeficients ātri nostabilizējas līdz konstantei. Galu galā viss būs daudz vienkāršāk. Mums vispār nav vajadzīgas formulas no Kalmana teorijas, mums vienkārši jāizvēlas pieņemama vērtība un jāievieto iteratīvajā formulā:

Nākamajā diagrammā parādīti dati, kas filtrēti divos dažādos veidos no fiktīva sensora. Ar nosacījumu, ka mēs neko nezinām par fenomena fiziku. Pirmā metode ir godīga, ar visām Kalmana teorijas formulām. Un otrais ir vienkāršots, bez formulām.

Kā redzam, metodes gandrīz neatšķiras. Neliela atšķirība vērojama tikai sākumā, kad Kalmana koeficients vēl nav nostabilizējies.

Diskusija

Kā mēs redzējām, Kalmana filtra galvenā ideja ir atrast tādu koeficientu, kas atbilst filtrētajai vērtībai

vidēji vismazāk atšķirtos no koordinātes reālās vērtības. Mēs redzam, ka filtrētā vērtība ir sensora nolasījuma un iepriekšējās filtrētās vērtības lineāra funkcija. Un iepriekšējā filtrētā vērtība, savukārt, ir sensora nolasījuma un iepriekšējās filtrētās vērtības lineāra funkcija. Un tā tālāk, līdz ķēde ir pilnībā apgriezta. Tas ir, filtrētā vērtība ir atkarīga no visi Iepriekšējie sensora rādījumi lineāri:

Tāpēc Kalmana filtru sauc par lineāro filtru.
Var pierādīt, ka no visiem lineārajiem filtriem Kalman filtrs ir labākais. Labākais tādā ziņā, ka filtra vidējā kļūda kvadrātā ir minimāla.

Daudzdimensionāls gadījums

Visu Kalmana filtra teoriju var vispārināt daudzdimensiju gadījumā. Tur esošās formulas izskatās nedaudz biedējošākas, taču ideja par to atvasināšanu ir tāda pati kā viendimensijas gadījumā. Jūs varat tos redzēt šajā brīnišķīgajā rakstā: http://habrahabr.ru/post/140274/.
Un šajā brīnišķīgajā video Ir sniegts to izmantošanas piemērs.