Atrodiet funkcijas nulles reizinājumu. Funkcija null. Periodiska funkcija. Funkcijas periods

2. Atradīsim nulles funkcijas.

f(x) pie x .

Atbildiet f(x) pie x .

2) x 2 > -4x-5;

x 2 +4x +5>0;

Ļaujiet f(x)=x 2 +4x +5, tad atradīsim tādu x, kuram f(x)>0,

D=-4 Nav nulles.

4. Nevienlīdzību sistēmas. Nevienādības un nevienādību sistēmas ar diviem mainīgajiem

1) Nevienādību sistēmas risinājumu kopa ir tajā ietverto nevienādību risinājumu kopu krustpunkts.

2) Nevienādības f(x;y)>0 atrisinājumu kopu var grafiski attēlot uz koordinātu plaknes. Parasti taisne, kas definēta ar vienādojumu f(x;y) = 0, sadala plakni 2 daļās, no kurām viena ir nevienādības atrisinājums. Lai noteiktu, kuru daļu, nevienādībā jāaizstāj patvaļīga punkta M(x0;y0), kas neatrodas uz taisnes f(x;y)=0, koordinātas. Ja f(x0;y0) > 0, tad nevienādības atrisinājums ir plaknes daļa, kurā atrodas punkts M0. ja f(x0;y0)<0, то другая часть плоскости.

3) Nevienādību sistēmas risinājumu kopa ir tajā ietverto nevienādību risinājumu kopu krustpunkts. Piemēram, dosim nevienlīdzību sistēmu:

.

Pirmajai nevienādībai risinājumu kopa ir aplis ar rādiusu 2 un kura centrs ir sākuma punktā, bet otrajai tā ir pusplakne, kas atrodas virs taisnes 2x+3y=0. Šīs sistēmas risinājumu kopa ir šo kopu krustpunkts, t.i. puslokā.

4) Piemērs. Atrisiniet nevienādību sistēmu:

1. nevienādības atrisinājums ir kopa , 2. ir kopa (2;7) un trešā ir kopa .

Šo kopu krustpunkts ir intervāls (2;3]), kas ir nevienādību sistēmas atrisinājumu kopa.

5. Racionālo nevienādību risināšana, izmantojot intervālu metodi

Intervālu metode balstās uz šādu binoma (x-a) īpašību: punkts x = α sadala skaitļa asi divās daļās - pa labi no punkta α binomāls (x-α)>0, un pa kreisi no punkta α (x-α)<0.

Lai jāatrisina nevienādība (x-α 1)(x-α 2)...(x-α n)>0, kur fiksēti α 1, α 2 ...α n-1, α n skaitļi, starp kuriem nav vienādu, un tādi, ka α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0, izmantojot intervālu metodi, rīkojas šādi: uz skaitliskās ass tiek uzzīmēti skaitļi α 1, α 2 ...α n-1, α n; intervālā pa labi no lielākās no tām, t.i. skaitļus α n, ielieciet plusa zīmi, tai sekojošajā intervālā no labās uz kreiso ielieciet mīnusa zīmi, tad plus zīmi, tad mīnusa zīmi utt. Tad visu nevienādības (x-α 1)(x-α 2)...(x-α n)>0 atrisinājumu kopa būs visu intervālu savienība, kurā ievietota pluszīme, un kopa nevienādības (x-α 1 )(x-α 2)...(x-α n) atrisinājumi<0 будет объединение всех промежутков, в которых поставлен знак «минус».

1) Racionālu nevienādību (t.i. formas nevienādību) risināšana P(x) Q(x), kur ir polinomi), balstās uz šādu nepārtrauktas funkcijas īpašību: ja nepārtraukta funkcija pazūd punktos x1 un x2 (x1; x2) un tai starp šiem punktiem nav citu sakņu, tad intervālos (x1; x2) funkcija saglabā savu zīmi.

Tāpēc, lai uz skaitļu līnijas atrastu funkcijas y=f(x) konstantes zīmes intervālus, atzīmējiet visus punktus, kuros funkcija f(x) pazūd vai tiek pārtraukta. Šie punkti sadala skaitļa līniju vairākos intervālos, kuru iekšpusē funkcija f(x) ir nepārtraukta un nepazūd, t.i. saglabā zīmi. Lai noteiktu šo zīmi, pietiek atrast funkcijas zīmi jebkurā aplūkojamā skaitļu līnijas intervāla punktā.

2) Noteikt racionālas funkcijas konstantes zīmes intervālus, t.i. Lai atrisinātu racionālu nevienādību, uz skaitļu līnijas atzīmējam skaitītāja saknes un saucēja saknes, kas vienlaikus ir arī racionālās funkcijas saknes un pārtraukuma punkti.

Nevienādību risināšana, izmantojot intervālu metodi

3. < 20.

Risinājums. Pieņemamo vērtību diapazonu nosaka nevienlīdzību sistēma:

Funkcijai f(x) = – 20. Atrodiet f(x):

kur x = 29 un x = 13.

f(30) = – 20 = 0,3 > 0,

f(5) = – 1 – 20 = – 10< 0.

Atbilde: . Pamatmetodes racionālu vienādojumu risināšanai. 1) Vienkāršākais: atrisināts ar parastajiem vienkāršojumiem - reducēšana līdz kopsaucējam, līdzīgu terminu samazināšana utt. Kvadrātvienādojumus ax2 + bx + c = 0 atrisina...

X mainās intervālā (0,1] un samazinās intervālā .

Mēs redzam, ka tas tiek pievienots n uz argumentu x, nemainās

funkcijas vērtība. Mazākais skaitlis, kas nav nulles skaitlis

no n ir , tāpēc šis ir periods sin 2 x .

Funkcijas nulles. Tiek izsaukta argumenta vērtība, pie kuras funkcija ir vienāda ar 0 nulle ( saknes) funkcija. Funkcijai var būt vairākas nulles. Piemēram, funkcija y = x (x + 1) (x- 3) ir trīs nulles: x = 0, x = — 1, x= 3. Ģeometriski nulles funkcija – tā ir funkcijas grafika un asi krustošanās punkta abscisa X .

7. attēlā parādīts funkcijas grafiks ar nullēm: x = a , x = b Un x = c .

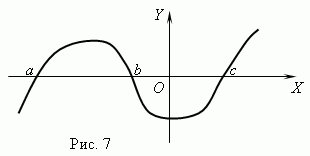
Asimptote. Ja funkcijas grafiks bezgalīgi tuvojas noteiktai taisnei, attālinoties no sākuma, tad šo līniju sauc asimptote.

6. tēma. “Intervāla metode”.

Ja f (x) f (x 0) x x 0, tad tiek izsaukta funkcija f (x). nepārtraukts punktā x 0.

Ja funkcija ir nepārtraukta katrā intervāla I punktā, tad to sauc nepārtraukti intervālā I (intervālu I sauc funkcijas nepārtrauktības intervāls). Funkcijas grafiks šajā intervālā ir nepārtraukta līnija, kuru, pēc viņu domām, var “uzzīmēt, nepaceļot zīmuli no papīra”.

Nepārtraukto funkciju īpašība.

Ja intervālā (a ; b) funkcija f ir nepārtraukta un nepazūd, tad šajā intervālā tā saglabā nemainīgu zīmi.

Uz šo īpašību ir balstīta metode nevienādību ar vienu mainīgo risināšanai, intervālu metode. Lai funkcija f(x) ir nepārtraukta intervālā I un izzūd ierobežotā punktu skaitā šajā intervālā. Pēc nepārtrauktu funkciju īpašībām šie punkti sadala I intervālos, kuros katrā nepārtrauktā funkcija f(x) c saglabā nemainīgu zīmi. Lai noteiktu šo zīmi, pietiek aprēķināt funkcijas f(x) vērtību jebkurā vienā punktā no katra šāda intervāla. Pamatojoties uz to, mēs iegūstam šādu algoritmu nevienādību risināšanai, izmantojot intervālu metodi.

Intervālu metode formas nevienādībām

Intervāla metode. Vidējais līmenis.

Vēlies pārbaudīt savus spēkus un uzzināt rezultātu, cik gatavs esi vienotajam valsts eksāmenam vai vienotajam valsts eksāmenam?

Lineāra funkcija

Formas funkciju sauc par lineāru. Kā piemēru ņemsim funkciju. Tas ir pozitīvs pie 3″> un negatīvs pie. Punkts ir funkcijas () nulle. Parādīsim šīs funkcijas zīmes uz skaitļu ass:

Mēs sakām, ka "funkcija maina zīmi, ejot caur punktu".

Redzams, ka funkcijas zīmes atbilst funkcijas grafika novietojumam: ja grafiks atrodas virs ass, zīme ir “ ”, ja zem tās ir “ ”.

Ja iegūto noteikumu vispārinām uz patvaļīgu lineārā funkcija, mēs iegūstam šādu algoritmu:

Kvadrātiskā funkcija

Es ceru, ka atceraties, kā atrisināt kvadrātvienādības? Ja nē, izlasiet tēmu “Kvadrātiskās nevienlīdzības”. Ļaujiet man jums atgādināt vispārējā forma kvadrātiskā funkcija: .

Tagad atcerēsimies, kādas zīmes aizņem kvadrātiskā funkcija. Tās grafiks ir parabola, un funkcija izmanto zīmi " " tiem, kuros parabola atrodas virs ass, un " " - ja parabola atrodas zem ass:

Ja funkcijai ir nulles (vērtības, pie kurām), parabola krustojas ar asi divos punktos - atbilstošā kvadrātvienādojuma saknēs. Tādējādi ass ir sadalīta trīs intervālos, un funkcijas zīmes pārmaiņus mainās, ejot cauri katrai saknei.

Vai ir iespējams kaut kā noteikt zīmes, katru reizi nezīmējot parabolu?

Atcerieties, ka kvadrātveida trinomu var faktorizēt:

Atzīmēsim saknes uz ass:

Mēs atceramies, ka funkcijas zīme var mainīties tikai tad, kad iet caur sakni. Izmantosim šo faktu: katram no trim intervāliem, kuros ass ir sadalīta ar saknēm, pietiek noteikt funkcijas zīmi tikai vienā patvaļīgi izvēlētā punktā: pārējos intervāla punktos zīme būs vienāda. .

Mūsu piemērā: pie 3″> abas izteiksmes iekavās ir pozitīvas (aizstāj, piemēram: 0″>). Uz ass ievietojam zīmi “ ”:

Ja (piemēram, aizstājējs), abas iekavas ir negatīvas, kas nozīmē, ka produkts ir pozitīvs:

Tā tas ir intervāla metode: zinot faktoru zīmes katrā intervālā, mēs nosakām visa produkta zīmi.

Apskatīsim arī gadījumus, kad funkcijai nav nulles vai ir tikai viena.

Ja viņu nav, tad nav arī sakņu. Tas nozīmē, ka nebūs nekādas “iekļūšanas caur sakni”. Tas nozīmē, ka funkcija aizņem tikai vienu zīmi visā skaitļu rindā. To var viegli noteikt, aizstājot to ar funkciju.

Ja ir tikai viena sakne, parabola pieskaras asij, tāpēc funkcijas zīme, ejot cauri saknei, nemainās. Kādu noteikumu mēs varam izdomāt šādām situācijām?

Ja ņem vērā šādu funkciju, iegūst divus identiskus faktorus:

Un jebkura kvadrātveida izteiksme nav negatīva! Tāpēc funkcijas zīme nemainās. Šādos gadījumos izcelsim sakni, kurai ejot cauri zīme nemainās, apvelkot to ar kvadrātu:

Mēs sauksim šādu sakni daudzkārtēji.

Intervālu metode nevienādībās

Tagad jebkuru kvadrātisko nevienādību var atrisināt, nezīmējot parabolu. Pietiek tikai novietot kvadrātfunkcijas zīmes uz ass un izvēlēties intervālus atkarībā no nevienādības zīmes. Piemēram:

Izmērīsim saknes uz ass un novietosim zīmes:

Mums ir vajadzīga ass daļa ar zīmi " "; tā kā nevienlīdzība nav stingra, risinājumā tiek iekļautas arī pašas saknes:

Tagad apsveriet racionālu nevienlīdzību - nevienlīdzību, kuras abas puses ir racionālas izteiksmes (skat. “Racionālie vienādojumi”).

Piemērs:

Visi faktori, izņemot vienu, šeit ir “lineāri”, tas ir, tie satur mainīgo tikai pirmajai pakāpei. Mums ir nepieciešami šādi lineārie faktori, lai piemērotu intervāla metodi - zīme mainās, ejot cauri to saknēm. Bet reizinātājam vispār nav sakņu. Tas nozīmē, ka tas vienmēr ir pozitīvs (pārbaudiet to paši), un tāpēc tas neietekmē visas nevienlīdzības zīmi. Tas nozīmē, ka mēs varam ar to sadalīt nevienlīdzības kreiso un labo pusi un tādējādi atbrīvoties no tās:

Tagad viss ir tāpat kā ar kvadrātvienādību: mēs nosakām, kuros punktos katrs no faktoriem kļūst par nulli, atzīmējam šos punktus uz ass un sakārtojam zīmes. Es vēlos vērst jūsu uzmanību uz ļoti svarīgu faktu:

Pāra skaitļa gadījumā rīkojamies tāpat kā iepriekš: punktu apvelkam ar kvadrātu un, izejot cauri saknei, zīmi nemainām. Bet nepāra skaitļa gadījumā šis noteikums nav spēkā: zīme joprojām mainīsies, izejot cauri saknei. Tāpēc mēs ar šādu sakni neko papildus nedarām, it kā tas nebūtu daudzkārtējs. Iepriekš minētie noteikumi attiecas uz visām pāra un nepāra pakāpēm.

Kas mums būtu jāraksta atbildē?

Ja tiek pārkāpta zīmju maiņa, jābūt ļoti uzmanīgiem, jo, ja nevienlīdzība nav stingra, atbildē jāiekļauj visi iekrāsotie punkti. Bet daži no tiem bieži izceļas, tas ir, tie nav iekļauti iekrāsotajā zonā. Šajā gadījumā mēs tos pievienojam atbildei kā izolētus punktus (cirtainos iekavās):

Piemēri (izlemiet paši):

Atbildes:

1. Ja starp faktoriem tas ir vienkāršs, tā ir sakne, jo to var attēlot kā.
   .

Funkcijas matemātiskais attēlojums skaidri parāda, kā viens lielums pilnībā nosaka cita lieluma vērtību. Tradicionāli tiek uzskatītas skaitliskās funkcijas, kas piešķir vienu numuru citam. Funkcijas nulle parasti ir tā argumenta vērtība, pie kuras funkcija kļūst par nulli.

Instrukcijas

1. Lai noteiktu funkcijas nulles, tās labā puse ir jāpielīdzina nullei un jāatrisina iegūtais vienādojums. Iedomāsimies, ka jums ir dota funkcija f(x)=x-5.

2. Lai atrastu šīs funkcijas nulles, ņemsim un pielīdzināsim tās labo pusi nullei: x-5=0.

3. Atrisinot šo vienādojumu, mēs atklājam, ka x=5 un šī argumenta vērtība būs funkcijas nulle. Tas ir, ja argumenta vērtība ir 5, funkcija f(x) kļūst par nulli.

Zem skata funkcijas matemātikā saprotam kopu elementu saistību. Pareizāk sakot, tas ir “likums”, saskaņā ar kuru viss vienas kopas elements (ko sauc par definīcijas domēnu) ir saistīts ar noteiktu citas kopas elementu (ko sauc par vērtību domēnu).

Jums būs nepieciešams

• Zināšanas algebrā un matemātiskajā apskatā.

Instrukcijas

1. Vērtības funkcijasŠī ir noteikta zona, no kuras funkcija var iegūt vērtības. Teiksim, vērtību diapazons funkcijas f(x)=|x| no 0 līdz bezgalībai. Lai atklātu nozīmē funkcijas noteiktā brīdī arguments ir jāaizstāj funkcijas tā skaitliskais ekvivalents, iegūtais skaitlis būs nozīmē m funkcijas. Ļaujiet funkcijai f(x)=|x| – 10 + 4x. Noskaidrosim nozīmē funkcijas punktā x=-2. Aizstāsim x ar skaitli -2: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16. Tas ir nozīmē funkcijas punktā -2 ir vienāds ar -16.

Piezīme!
Pirms funkcijas vērtības meklēšanas punktā pārliecinieties, vai tā atrodas funkcijas domēnā.

Noderīgs padoms
Līdzīga metode ļauj atklāt vairāku argumentu funkcijas nozīmi. Atšķirība ir tāda, ka viena skaitļa vietā jums būs jāaizstāj vairāki - atbilstoši funkcijas argumentu skaitam.

Funkcija attēlo izveidoto savienojumu starp mainīgo y un mainīgo x. Turklāt visas x vērtības, ko sauc par argumentu, atbilst y izņēmuma vērtībai - funkcijai. Grafiskā formā funkcija ir attēlota uz Dekarta koordinātu sistēmas grafika veidā. Grafika krustošanās punktus ar abscisu asi, uz kuriem uzzīmēti argumenti x, sauc par funkcijas nullēm. Pieņemamu nulles atrašana ir viens no uzdevumiem, lai atrastu doto funkciju. Šajā gadījumā tiek ņemtas vērā visas neatkarīgā mainīgā x pieļaujamās vērtības, kas veido funkcijas definīcijas domēnu (DOF).

Instrukcijas

1. Funkcijas nulle ir argumenta x vērtība, pie kuras funkcijas vērtība ir vienāda ar nulli. Tomēr tikai tie argumenti, kas ietilpst pētāmās funkcijas definīcijas ietvaros, var būt nulles. Tas ir, ir daudz vērtību, kurām funkcija f(x) ir noderīga.

2. Pierakstiet doto funkciju un pielīdziniet to nullei, teiksim f(x) = 2x?+5x+2 = 0. Atrisiniet iegūto vienādojumu un atrodiet tā reālās saknes. Kvadrātvienādojuma saknes aprēķina ar atbalstu diskriminanta atrašanai. 2x?+5x+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0,5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2. Tādējādi šajā gadījumā tiek iegūtas divas kvadrātvienādojuma saknes, kas atbilst sākotnējās funkcijas f(x) argumenti.

3. Pārbaudiet, vai visas konstatētās x vērtības pieder dotās funkcijas definīcijas domēnam. Noskaidrojiet OOF, lai to izdarītu, pārbaudiet sākotnējo izteiksmi formas?f (x) pāra sakņu klātbūtnei, daļskaitļu klātbūtnei funkcijā ar argumentu saucējā, logaritmisko vai trigonometrisko klātbūtni. izteiksmes.

4. Apsverot funkciju ar izteiksmi zem pāra pakāpes saknes, par definīcijas domēnu ņemiet visus argumentus x, kuru vērtības nepārvērš radikālo izteiksmi par negatīvu skaitli (tieši otrādi, funkcija to dara nav jēgas). Pārbaudiet, vai funkcijas noteiktās nulles ietilpst noteiktā pieņemamo x vērtību diapazonā.

5. Daļas saucējs nevar būt nulle, tāpēc izslēdziet tos argumentus x, kas noved pie šāda rezultāta. Logaritmiskiem lielumiem jāņem vērā tikai tās argumenta vērtības, kurām pati izteiksme ir lielāka par nulli. Funkcijas nulles, kas pārvērš sublogaritmisko izteiksmi par nulli vai negatīvu skaitli, ir jāizmet no gala rezultāta.

Piezīme!
Atrodot vienādojuma saknes, var parādīties papildu saknes. To ir viegli pārbaudīt: vienkārši aizstājiet iegūto argumenta vērtību funkcijā un pārliecinieties, vai funkcija pārvēršas par nulli.

Noderīgs padoms
Reizēm funkcija nav skaidri izteikta ar argumentu palīdzību, tāpēc ir viegli uzzināt, kas ir šī funkcija. Piemērs tam ir apļa vienādojums.

Argumentu vērtības z pie kura f(z) pāriet uz nulli sauc. nulles punkts, t.i. Ja f(a) = 0, tad a - nulles punkts.

Def. Punkts A sauca nulles kārtīban , Ja FKP var pārstāvēt formā f(z) = , kur
analītiskā funkcija un
0.

Šajā gadījumā Teilora sērijas funkcijas paplašināšana (43) ir pirmā n koeficienti ir nulle

= =

utt. Nosakiet nulles secību
un (1 – cos z) plkst z = 0

=
=

nulle 1.kārta

1 – cos z =
=

nulle 2.kārta

Def. Punkts z =
sauca punkts bezgalībā Un nulle funkcijas f(z), Ja f(
) = 0. Šādu funkciju var izvērst virknē negatīvos pakāpēs z : f(z) =
. Ja vispirms n koeficienti ir vienādi ar nulli, tad mēs nonākam pie nulles kārtība n punktā bezgalībā: f(z) = z - n
.

Izolētie vienskaitļa punkti ir sadalīti: a) noņemami atsevišķi punkti; b) kārtības stabin; V) būtībā vienskaitlī punkti.

Punkts A sauca noņemams vienskaitlis punkts funkcijas f(z) ja plkst z
a lim f(z) = Ar - galīgais numurs .

Punkts A sauca kārtības stabsn (n 1) funkcijas f(z), ja apgrieztā funkcija
= 1/ f(z) ir nulles secība n punktā A.Šādu funkciju vienmēr var attēlot kā f(z) =
, Kur
- analītiskā funkcija un
.

Punkts A sauca būtībā īpašs punkts funkcijas f(z), ja plkst z
a lim f(z) neeksistē.

Laurent sērija

Apskatīsim gredzena konverģences reģiona gadījumu r < | z 0 – a| < R centrēts punktā A funkcijai f(z). Ieviesīsim divus jaunus lokus L 1 (r) Un L 2 (R) netālu no gredzena robežām ar punktu z 0 starp tām. Izgriezīsim gredzenu, savienosim apļus gar griezuma malām, pāriesim uz vienkārši savienotu apgabalu un

Košī integrāļa formula (39) iegūstam divus integrāļus virs mainīgā z

f(z 0) =
+
, (42)

kur integrācija notiek pretējos virzienos.

Par integrāli beidzies L 1 nosacījums ir izpildīts | z 0 – a | > | z – a |, un integrālam over L 2 apgriezts nosacījums | z 0 – a | < | z – a |. Tāpēc koeficients 1/( z – z 0) izvērst sērijā (a) integrāļa virs L 2 un sērijā (b) integrālī virs L 1 . Rezultātā mēs iegūstam paplašināšanos f(z) gredzena zonā iekšā Laurent sērija ar pozitīvajām un negatīvajām spējām ( z 0 – a)

f(z 0) =
A n (z 0 -a) n (43)

Kur A n =
=
;A -n =

Pozitīvo spēku paplašināšanās (z 0 - A) sauca labā daļa Laurent sērija (Taylor sērija), un tiek saukta negatīvo spēku izplešanās. galvenā daļa Laurent sērija.

Ja apļa iekšpusē L 1 nav vienskaitļa punktu un funkcija ir analītiska, tad (44) pirmais integrālis ir vienāds ar nulli pēc Košī teorēmas un funkcijas izvērsumā paliek tikai pareizā daļa. Negatīvās spējas izvērsumā (45) parādās tikai tad, ja iekšējā apļa ietvaros tiek pārkāpta analītiskā spēja, un tās kalpo, lai aprakstītu funkciju izolētu vienskaitļa punktu tuvumā.

Lai izveidotu Laurent sēriju (45) priekš f(z) varat aprēķināt izplešanās koeficientus, izmantojot vispārīgu formulu vai izmantot elementāro funkciju paplašinājumus, kas iekļauti f(z).

Terminu skaits ( n) no Laurent sērijas galvenās daļas ir atkarīgs no vienskaitļa punkta veida: noņemams vienskaitlis punkts (n = 0) ; būtībā vienskaitlis punkts (n
); stabsn- wow pasūtījums(n - gala numurs).

un priekš f(z) = punkts z = 0 noņemams vienskaitlis, jo nav galvenās daļas. f(z) = (z -
) = 1 -

b) priekš f(z) = punkts z = 0 - 1. kārtas stabs

f(z) = (z -
) = -

c) priekš f(z) = e 1 / z punkts z = 0 - būtībā vienskaitlis punkts

f(z) = e 1 / z =

Ja f(z) ir analītisks šajā jomā D izņemot m izolēti vienskaitļa punkti un | z 1 | < |z 2 | < . . . < |z m| , tad paplašinot funkciju pakāpēs z visa plakne ir sadalīta m+ 1 gredzens | z i | < | z | < | z i+ 1 | un Laurent sērija ir dažāda veida katram gredzenam. Paplašinot pilnvaras ( z – z i ) Laurent rindas konverģences apgabals ir aplis | z – z i | < r, Kur r – attālums līdz tuvākajam vienskaitļa punktam.

utt. Paplašināsim funkciju f(z) =Laurent sērijā pilnvarās z Un ( z - 1).

Risinājums. Attēlosim funkciju formā f(z) = - z 2 . Mēs izmantojam formulu ģeometriskās progresijas summai
. Aplī |z|< 1 ряд сходится и f(z) = - z 2 (1 + z + z 2 + z 3 + z 4 + . . .) = - z 2 - z 3 - z 4 - . . . , t.i. sadalīšanās satur tikai pareizi daļa. Pārejam uz apļa |z| ārējo apgabalu > 1. Attēlosim funkciju formā
, kur 1/| z| < 1, и получим разложение f(z) = z
=z + 1 +

Jo , funkcijas paplašināšana pilnvarās ( z - 1) izskatās f(z) = (z - 1) -1 + 2 + (z - 1) visiem
1.

utt. Paplašiniet funkciju Laurent sērijā f(z) =
: a) pēc grādiem z aplī | z| < 1; b) по степеням z gredzens 1< |z| < 3 ; c) по степеням (z – 2).Risinājums. Sadalīsim funkciju vienkāršās daļās
= =+=
. No apstākļiem z =1
A = -1/2 , z =3
B = ½.

A) f(z) = ½ [
] = ½ [
-(1/3)
], ar | z|< 1.

b) f(z) = - ½ [
+
] = - (
), plkst.1< |z| < 3.

ar) f(z) = ½ [
]= - ½ [
] =

= - ½ = -
, ar |2 - z| < 1

Tas ir aplis ar rādiusu 1, kura centrs ir z = 2 .

Dažos gadījumos jaudas rindas var reducēt līdz ģeometrisko progresiju kopai, un pēc tam ir viegli noteikt to konverģences reģionu.

utt. Izpētiet rindu konverģenci

. . . + + + + 1 + () + () 2 + () 3 + . . .

Risinājums. Šī ir divu ģeometrisko progresiju summa ar q 1 = , q 2 = () . No to konverģences nosacījumiem izriet < 1 , < 1 или |z| > 1 , |z| < 2 , т.е. область сходимости ряда кольцо 1 < |z| < 2 .

Kas ir funkciju nulles? Atbilde ir pavisam vienkārša – tas ir matemātisks termins, kas apzīmē dotās funkcijas definīcijas apgabalu, kurā tās vērtība ir nulle. Funkcijas nulles tiek sauktas arī par nullēm. Vienkāršākais veids, kā izskaidrot, kas ir funkcijas nulles, ir ar dažiem vienkāršiem piemēriem.

Piemēri

Apskatīsim vienkāršo vienādojumu y=x+3. Tā kā funkcijas nulle ir tā argumenta vērtība, kurā y ieguva nulles vērtību, vienādojuma kreisajā pusē mēs aizstājam ar 0:

Šajā gadījumā -3 ir vēlamā nulle. Noteiktai funkcijai ir tikai viena vienādojuma sakne, bet tas ne vienmēr tā ir.

Apskatīsim citu piemēru:

Aizstāsim 0 vienādojuma kreisajā pusē, tāpat kā iepriekšējā piemērā:

Acīmredzot šajā gadījumā būs divas funkcijas nulles: x=3 un x=-3. Ja vienādojumam būtu trešās pakāpes arguments, būtu trīs nulles. Var izdarīt vienkāršu secinājumu, ka polinoma sakņu skaits atbilst argumenta maksimālajai pakāpei vienādojumā. Tomēr daudzas funkcijas, piemēram, y = x 3, no pirmā acu uzmetiena ir pretrunā ar šo apgalvojumu. Loģika un veselais saprāts liecina, ka šai funkcijai ir tikai viena nulle - punktā x=0. Bet patiesībā ir trīs saknes, tās vienkārši visas sakrīt. Ja atrisināsit vienādojumu sarežģītā formā, tas kļūst acīmredzams. x=0 šajā gadījumā sakne, kuras reizinājums ir 3. Iepriekšējā piemērā nulles nesakrita, tāpēc tām bija reizinājums 1.

Noteikšanas algoritms

No sniegtajiem piemēriem varat redzēt, kā noteikt funkcijas nulles. Algoritms vienmēr ir vienāds:

1. Uzrakstiet funkciju.
2. Aizstāj y vai f(x)=0.
3. Atrisiniet iegūto vienādojumu.

Pēdējā punkta grūtības pakāpe ir atkarīga no vienādojuma argumentācijas pakāpes. Risinot augstas pakāpes vienādojumus, ir īpaši svarīgi atcerēties, ka vienādojuma sakņu skaits ir vienāds ar argumenta maksimālo pakāpi. Tas jo īpaši attiecas uz trigonometriskajiem vienādojumiem, kur, sadalot abas puses ar sinusu vai kosinusu, tiek zaudētas saknes.

Patvaļīgas pakāpes vienādojumus visvieglāk atrisināt, izmantojot Hornera metodi, kas tika izstrādāta īpaši patvaļīga polinoma nulles atrašanai.

Funkciju nulles vērtība var būt negatīva vai pozitīva, reāla vai kompleksā plaknē, vienskaitlī vai daudzkārtēja. Vai arī vienādojumam var nebūt sakņu. Piemēram, funkcija y=8 neiegūs nulles vērtību nevienam x, jo tā nav atkarīga no šī mainīgā.

Vienādojumam y=x 2 -16 ir divas saknes, un abas atrodas kompleksajā plaknē: x 1 =4i, x 2 =-4i.

Biežas kļūdas

Bieža kļūda, ko pieļauj skolēni, kuri vēl nav pilnībā sapratuši, kas ir funkcijas nulles, ir argumenta (x) aizstāšana ar nulli, nevis funkcijas vērtību (y). Viņi pārliecinoši aizstāj x=0 vienādojumā un, pamatojoties uz to, atrod y. Bet šī ir nepareiza pieeja.

Vēl viena kļūda, kā jau minēts, ir samazināšana ar sinusu vai kosinusu trigonometriskā vienādojumā, kādēļ tiek zaudēta viena vai vairākas funkcijas nulles. Tas nenozīmē, ka šādos vienādojumos neko nevar samazināt, bet turpmākajos aprēķinos ir jāņem vērā šie “pazaudētie” faktori.

Grafiskais attēlojums

Varat saprast, kādas ir funkcijas nulles, izmantojot matemātiskās programmas, piemēram, Maple. Tajā var izveidot grafiku, norādot vēlamo punktu skaitu un vēlamo mērogu. Tie punkti, kuros grafiks krustojas ar OX asi, ir vēlamās nulles. Šis ir viens no visvairāk ātri veidi polinoma sakņu atrašana, īpaši, ja tā secība ir augstāka par trešo. Tātad, ja ir nepieciešams regulāri veikt matemātiskus aprēķinus, atrast patvaļīgu grādu polinomu saknes, veidot grafikus, Maple vai līdzīga programma būs vienkārši neaizstājama aprēķinu veikšanai un pārbaudei.