ค้นหาผลคูณของศูนย์ของฟังก์ชัน ฟังก์ชันเป็นโมฆะ ฟังก์ชันคาบ ระยะเวลาการทำงาน

2. มาหาศูนย์กันดีกว่าฟังก์ชั่น.

ฉ(x) ที่ x .

ตอบ f(x) ที่ x .

2) x 2 >-4x-5;

x 2 +4x +5>0;

ให้ f(x)=x 2 +4x +5 แล้วให้เราหา x โดยที่ f(x)>0,

D=-4 ไม่มีศูนย์

4. ระบบความไม่เท่าเทียมกัน อสมการและระบบอสมการที่มีตัวแปรสองตัว

1) ชุดวิธีแก้ปัญหาสำหรับระบบความไม่เท่าเทียมกันคือจุดตัดของชุดวิธีแก้ปัญหาสำหรับความไม่เท่าเทียมกันที่รวมอยู่ในนั้น

2) ชุดของการแก้อสมการ f(x;y)>0 สามารถแสดงเป็นภาพกราฟิกบนระนาบพิกัดได้ โดยทั่วไป เส้นตรงที่กำหนดโดยสมการ f(x;y) = 0 จะแบ่งระนาบออกเป็น 2 ส่วน หนึ่งในนั้นคือคำตอบของอสมการ ในการพิจารณาว่าส่วนใด คุณต้องแทนที่พิกัดของจุดใดก็ได้ M(x0;y0) ที่ไม่ได้อยู่บนเส้น f(x;y)=0 ไปเป็นอสมการ ถ้า f(x0;y0) > 0 ดังนั้นคำตอบของอสมการคือส่วนของระนาบที่มีจุด M0 ถ้าฉ(x0;y0)<0, то другая часть плоскости.

3) ชุดวิธีแก้ปัญหาสำหรับระบบความไม่เท่าเทียมกันคือจุดตัดของชุดวิธีแก้ปัญหาสำหรับความไม่เท่าเทียมกันที่รวมอยู่ในนั้น ตัวอย่างเช่น ให้ระบบความไม่เท่าเทียมกัน:

.

สำหรับอสมการแรก เซตของคำตอบคือวงกลมรัศมี 2 และมีศูนย์กลางอยู่ที่จุดกำเนิด และเซตที่สองคือระนาบครึ่งระนาบที่อยู่เหนือเส้นตรง 2x+3y=0 ชุดวิธีแก้ปัญหาของระบบนี้คือจุดตัดของชุดเหล่านี้ เช่น ครึ่งวงกลม

4) ตัวอย่าง แก้ระบบอสมการ:

วิธีแก้อสมการที่ 1 คือ เซต เซตที่ 2 คือเซต (2;7) และเซตที่สามคือเซต

จุดตัดของเซตเหล่านี้คือช่วง (2;3) ซึ่งเป็นเซตของการแก้ระบบอสมการ

5. การแก้อสมการเชิงเหตุผลโดยใช้วิธีช่วงเวลา

วิธีการกำหนดช่วงเวลาขึ้นอยู่กับคุณสมบัติของทวินาม (x-a) ต่อไปนี้ จุด x = α แบ่งแกนตัวเลขออกเป็นสองส่วน - ทางด้านขวาของจุด α คือทวินาม (x-α)>0 และไปทางขวาของจุด α คือทวินาม (x-α)>0 และไปที่ ทางซ้ายของจุด α (x-α)<0.

ปล่อยให้จำเป็นต้องแก้อสมการ (x-α 1)(x-α 2)...(x-α n)>0 โดยที่ α 1, α 2 ...α n-1, α n ได้รับการแก้ไขแล้ว ตัวเลขซึ่งในจำนวนนี้ไม่มีค่าเท่ากัน และเช่นนั้น α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 โดยใช้วิธีการช่วงเวลา ดำเนินการดังนี้: ตัวเลข α 1, α 2 ...α n-1, α n ถูกพล็อตบนแกนตัวเลข ในช่วงเวลาทางด้านขวาของช่วงที่ใหญ่ที่สุดคือ ตัวเลข α n ใส่เครื่องหมายบวก ในช่วงต่อจากขวาไปซ้าย ให้ใส่เครื่องหมายลบ จากนั้นจึงใส่เครื่องหมายบวก จากนั้นจึงใส่เครื่องหมายลบ ฯลฯ จากนั้นเซตของคำตอบทั้งหมดสำหรับอสมการ (x-α 1)(x‑α 2)...(x-α n)>0 จะเป็นการรวมกันของช่วงทั้งหมดที่มีเครื่องหมายบวกวางไว้ และเซต ของการแก้อสมการ (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».

1) การแก้ความไม่เท่าเทียมกันเชิงเหตุผล (เช่น ความไม่เท่าเทียมกันของแบบฟอร์ม P(x) Q(x) โดยที่พหุนาม) ขึ้นอยู่กับคุณสมบัติของฟังก์ชันต่อเนื่องต่อไปนี้: ถ้าฟังก์ชันต่อเนื่องหายไปที่จุด x1 และ x2 (x1; x2) และไม่มีรากอื่นระหว่างจุดเหล่านี้ แล้วใน ช่วงเวลา (x1; x2) ฟังก์ชันจะคงเครื่องหมายไว้

ดังนั้น หากต้องการค้นหาช่วงเวลาของเครื่องหมายคงที่ของฟังก์ชัน y=f(x) บนเส้นจำนวน ให้ทำเครื่องหมายทุกจุดที่ทำให้ฟังก์ชัน f(x) หายไปหรือเกิดความไม่ต่อเนื่อง จุดเหล่านี้จะแบ่งเส้นจำนวนออกเป็นหลายช่วง โดยในแต่ละช่วงจะมีฟังก์ชัน f(x) ต่อเนื่องกันและไม่หายไป กล่าวคือ บันทึกเครื่องหมาย ในการกำหนดเครื่องหมายนี้ก็เพียงพอแล้วที่จะค้นหาเครื่องหมายของฟังก์ชันที่จุดใดก็ได้ของช่วงเวลาที่พิจารณาของเส้นจำนวน

2) เพื่อกำหนดช่วงเวลาของเครื่องหมายคงที่ของฟังก์ชันตรรกยะ เช่น ในการแก้อสมการเชิงตรรกยะ เราจะทำเครื่องหมายรากของตัวเศษและรากของตัวส่วนไว้บนเส้นจำนวน ซึ่งเป็นรากและจุดพักของฟังก์ชันตรรกยะด้วย

การแก้ไขอสมการโดยใช้วิธีช่วงเวลา

3. < 20.

สารละลาย. ช่วงของค่าที่ยอมรับได้ถูกกำหนดโดยระบบความไม่เท่าเทียมกัน:

สำหรับฟังก์ชัน f(x) = – 20. หา f(x):

โดยที่ x = 29 และ x = 13

ฉ(30) = – 20 = 0.3 > 0,

ฉ(5) = – 1 – 20 = – 10< 0.

คำตอบ: . วิธีการพื้นฐานในการแก้สมการตรรกยะ 1) วิธีที่ง่ายที่สุด: แก้ไขได้โดยการทำให้เข้าใจง่ายตามปกติ - การลดลงเป็นตัวส่วนร่วม, การลดเงื่อนไขที่คล้ายกันและอื่น ๆ สมการกำลังสอง ax2 + bx + c = 0 แก้ได้โดย...

X เปลี่ยนแปลงในช่วงเวลา (0,1] และลดลงในช่วงเวลา

เราเห็นการเพิ่มนั้น nถึงข้อโต้แย้ง x,ไม่เปลี่ยนแปลง

ค่าฟังก์ชัน จำนวนที่ไม่เป็นศูนย์น้อยที่สุด

จาก nคือ ดังนั้นนี่คือช่วงเวลาบาป 2 x .

ฟังก์ชันศูนย์ ค่าอาร์กิวเมนต์ที่ฟังก์ชันเท่ากับ 0 เรียกว่า ศูนย์ ( ราก) ฟังก์ชัน. ฟังก์ชันอาจมีศูนย์หลายตัว ตัวอย่างเช่นฟังก์ชัน ย = x (x + 1) (x- 3) มีศูนย์สามตัว: x = 0, x = — 1, x= 3. ทางเรขาคณิต ฟังก์ชันว่าง – นี่คือจุดตัดของกราฟฟังก์ชันกับแกน เอ็กซ์ .

รูปที่ 7 แสดงกราฟของฟังก์ชันที่มีศูนย์: x = ก , x = ขและ x = ค .

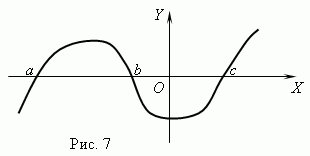
เส้นกำกับ หากกราฟของฟังก์ชันเข้าใกล้เส้นตรงเส้นหนึ่งอย่างไม่มีกำหนดขณะที่มันเคลื่อนออกจากจุดกำเนิด เส้นนี้จะถูกเรียกว่า เส้นกำกับ.

หัวข้อที่ 6 “วิธีการเว้นช่วง”

ถ้า f (x) f (x 0) สำหรับ x x 0 ฟังก์ชัน f (x) จะถูกเรียกใช้ ต่อเนื่องที่จุด x 0.

ถ้าฟังก์ชันมีความต่อเนื่องในทุกจุดของช่วงเวลา I ฟังก์ชันนั้นจะถูกเรียก อย่างต่อเนื่องตามช่วงเวลาฉัน (ช่วงที่ฉันเรียกว่า ช่วงความต่อเนื่องของฟังก์ชัน). กราฟของฟังก์ชันในช่วงเวลานี้เป็นเส้นต่อเนื่อง ซึ่งเขาบอกว่าสามารถ "วาดได้โดยไม่ต้องยกดินสอออกจากกระดาษ"

คุณสมบัติของฟังก์ชันต่อเนื่อง

หากในช่วงเวลา (a ; b) ฟังก์ชัน f ต่อเนื่องและไม่หายไป ฟังก์ชัน f จะคงเครื่องหมายคงที่ไว้ในช่วงเวลานี้

วิธีการแก้อสมการด้วยตัวแปรตัวเดียว ซึ่งก็คือวิธีช่วงเวลานั้นจะขึ้นอยู่กับคุณสมบัตินี้ ปล่อยให้ฟังก์ชัน f(x) ต่อเนื่องกันในช่วง I และหายไปตามจำนวนจุดที่กำหนดในช่วงเวลานี้ ตามคุณสมบัติของฟังก์ชันต่อเนื่อง จุดเหล่านี้จะแบ่ง I ออกเป็นช่วงๆ โดยแต่ละฟังก์ชันต่อเนื่อง f(x) c จะรักษาเครื่องหมายคงที่ไว้ ในการระบุเครื่องหมายนี้ ก็เพียงพอที่จะคำนวณค่าของฟังก์ชัน f(x) ที่จุดใดจุดหนึ่งจากแต่ละช่วงเวลาดังกล่าว จากข้อมูลนี้ เราได้รับอัลกอริธึมต่อไปนี้สำหรับการแก้ไขอสมการโดยใช้วิธีช่วงเวลา

วิธีช่วงเวลาสำหรับความไม่เท่าเทียมกันของแบบฟอร์ม

วิธีช่วงเวลา ระดับเฉลี่ย.

คุณต้องการทดสอบความแข็งแกร่งของคุณและดูว่าคุณพร้อมแค่ไหนสำหรับการสอบ Unified State หรือ Unified State?

ฟังก์ชันเชิงเส้น

ฟังก์ชันของแบบฟอร์มเรียกว่าเชิงเส้น ลองใช้ฟังก์ชันเป็นตัวอย่าง เป็นบวกที่ 3″> และเป็นลบที่ จุดคือศูนย์ของฟังก์ชัน () เรามาแสดงสัญญาณของฟังก์ชันนี้บนแกนตัวเลข:

เราว่า “ฟังก์ชันจะเปลี่ยนเครื่องหมายเมื่อผ่านจุดนั้น”

จะเห็นได้ว่าสัญลักษณ์ของฟังก์ชันสอดคล้องกับตำแหน่งของกราฟฟังก์ชัน: หากกราฟอยู่เหนือแกน เครื่องหมายจะเป็น “ ” หากอยู่ด้านล่างคือ “ ”

หากเราสรุปกฎผลลัพธ์ให้เป็นกฎเกณฑ์ ฟังก์ชันเชิงเส้นเราได้รับอัลกอริธึมดังต่อไปนี้:

ฟังก์ชันกำลังสอง

ฉันหวังว่าคุณจะจำวิธีแก้อสมการกำลังสองได้ไหม ถ้าไม่ อ่านหัวข้อ “สมการกำลังสอง” ฉันขอเตือนคุณ แบบฟอร์มทั่วไปฟังก์ชันกำลังสอง: .

ทีนี้มาจำไว้ว่าฟังก์ชันกำลังสองมีสัญญาณอะไร กราฟของมันคือพาราโบลา และฟังก์ชันจะใช้เครื่องหมาย " " สำหรับพาราโบลาที่อยู่เหนือแกน และ " " - ถ้าพาราโบลาอยู่ต่ำกว่าแกน:

หากฟังก์ชันมีศูนย์ (ค่าที่) พาราโบลาจะตัดแกนที่จุดสองจุด - รากของสมการกำลังสองที่สอดคล้องกัน ดังนั้นแกนจึงถูกแบ่งออกเป็นสามช่วงและสัญญาณของฟังก์ชันจะเปลี่ยนไปสลับกันเมื่อผ่านแต่ละรูต

เป็นไปได้ไหมที่จะกำหนดสัญญาณโดยไม่ต้องวาดพาราโบลาทุกครั้ง?

โปรดจำไว้ว่าสามารถแยกตัวประกอบตรีโกณมิติกำลังสองได้:

ทำเครื่องหมายรากบนแกน:

เราจำได้ว่าเครื่องหมายของฟังก์ชันสามารถเปลี่ยนแปลงได้เมื่อผ่านรูทเท่านั้น ลองใช้ข้อเท็จจริงนี้: สำหรับแต่ละช่วงเวลาที่แกนถูกหารด้วยรากก็เพียงพอที่จะกำหนดเครื่องหมายของฟังก์ชันที่จุดที่เลือกโดยพลการเพียงจุดเดียวเท่านั้น: ที่จุดที่เหลือของช่วงเวลาเครื่องหมายจะเหมือนกัน .

ในตัวอย่างของเรา: ที่ 3″> นิพจน์ทั้งสองในวงเล็บเป็นบวก (แทนที่ เช่น: 0″>) เราใส่เครื่องหมาย " " ไว้บนแกน:

เมื่อ (เช่น แทนค่า) วงเล็บทั้งสองเป็นค่าลบ ซึ่งหมายความว่าผลคูณเป็นบวก:

นั่นคือสิ่งที่มันเป็น วิธีช่วงเวลา: เมื่อทราบสัญญาณของปัจจัยแต่ละช่วงแล้วเราจะกำหนดสัญญาณของผลิตภัณฑ์ทั้งหมด

ลองพิจารณากรณีที่ฟังก์ชันไม่มีศูนย์หรือมีเพียงอันเดียว

หากไม่มีก็ไม่มีราก ซึ่งหมายความว่าจะไม่มีการ "ผ่านราก" ซึ่งหมายความว่าฟังก์ชันจะใช้เครื่องหมายเดียวบนเส้นจำนวนทั้งหมด สามารถกำหนดได้อย่างง่ายดายโดยการแทนที่ลงในฟังก์ชัน

หากมีรากเพียงรากเดียว พาราโบลาจะแตะแกน ดังนั้นเครื่องหมายของฟังก์ชันจะไม่เปลี่ยนแปลงเมื่อผ่านราก เราจะคิดกฎอะไรได้บ้างสำหรับสถานการณ์เช่นนี้?

หากคุณแยกตัวประกอบฟังก์ชันดังกล่าว คุณจะได้ตัวประกอบที่เหมือนกันสองตัว:

และนิพจน์กำลังสองใดๆ ไม่เป็นลบ! ดังนั้นเครื่องหมายของฟังก์ชันจึงไม่เปลี่ยนแปลง ในกรณีเช่นนี้ เราจะเน้นรากเมื่อผ่านซึ่งเครื่องหมายไม่เปลี่ยนแปลง โดยวงกลมเป็นสี่เหลี่ยมจัตุรัส:

เราจะเรียกรูตดังกล่าว ทวีคูณ.

วิธีช่วงเวลาในอสมการ

ตอนนี้อสมการกำลังสองใดๆ ก็สามารถแก้ไขได้โดยไม่ต้องวาดพาราโบลา เพียงวางเครื่องหมายของฟังก์ชันกำลังสองบนแกนก็เพียงพอแล้วและเลือกช่วงเวลาขึ้นอยู่กับเครื่องหมายของความไม่เท่าเทียมกัน ตัวอย่างเช่น:

มาวัดรากบนแกนแล้ววางเครื่องหมาย:

เราต้องการส่วนของแกนที่มีเครื่องหมาย " " เนื่องจากความไม่เท่าเทียมกันไม่เข้มงวด รากจึงรวมอยู่ในการแก้ปัญหาด้วย:

ตอนนี้ให้พิจารณาความไม่เท่าเทียมกันเชิงเหตุผล - ความไม่เท่าเทียมกันซึ่งทั้งสองฝ่ายเป็นนิพจน์ที่มีเหตุผล (ดู "สมการเหตุผล")

ตัวอย่าง:

ปัจจัยทั้งหมดยกเว้นปัจจัยหนึ่งถือเป็น "เชิงเส้น" ในที่นี้ กล่าวคือ มีตัวแปรเฉพาะกำลังแรกเท่านั้น เราต้องการปัจจัยเชิงเส้นดังกล่าวเพื่อใช้วิธีช่วงเวลา - เครื่องหมายจะเปลี่ยนเมื่อผ่านรากของมัน แต่ตัวคูณไม่มีรากเลย ซึ่งหมายความว่าเป็นบวกเสมอ (ตรวจสอบด้วยตัวคุณเอง) และดังนั้นจึงไม่ส่งผลกระทบต่อสัญญาณของความไม่เท่าเทียมกันทั้งหมด ซึ่งหมายความว่าเราสามารถหารด้านซ้ายและด้านขวาของอสมการได้ และกำจัดมันออกไป:

ตอนนี้ทุกอย่างเหมือนเดิมกับอสมการกำลังสอง: เรากำหนดว่าแต่ละปัจจัยจะกลายเป็นศูนย์ที่จุดใด ทำเครื่องหมายจุดเหล่านี้บนแกนและจัดเรียงเครื่องหมาย ฉันต้องการดึงความสนใจของคุณไปยังข้อเท็จจริงที่สำคัญมาก:

ในกรณีของเลขคู่ เราทำเหมือนเดิม: เราวนจุดด้วยสี่เหลี่ยมจัตุรัสและไม่เปลี่ยนเครื่องหมายเมื่อผ่านรูท แต่ในกรณีของเลขคี่ กฎนี้ใช้ไม่ได้: เครื่องหมายจะยังคงเปลี่ยนเมื่อผ่านรูท ดังนั้นเราจึงไม่ทำอะไรเพิ่มเติมกับรูทดังกล่าว ราวกับว่ามันไม่ใช่จำนวนทวีคูณ กฎข้างต้นใช้กับเลขยกกำลังคู่และเลขคี่ทั้งหมด

เราควรเขียนอะไรในคำตอบ?

หากฝ่าฝืนการสลับป้ายต้องระวังให้มากเพราะถ้าความไม่เท่าเทียมกันไม่เข้มงวดคำตอบก็ควรประกอบด้วย จุดที่แรเงาทั้งหมด. แต่บางคนก็มักจะแยกจากกันนั่นคือไม่รวมอยู่ในพื้นที่สีเทา ในกรณีนี้ เราจะเพิ่มลงในคำตอบเป็นจุดแยก (ในวงเล็บปีกกา):

ตัวอย่าง (ตัดสินใจด้วยตัวเอง):

คำตอบ:

1. ถ้าในบรรดาปัจจัยต่างๆ มันง่าย มันเป็นราก เพราะสามารถแสดงเป็นได้
   .

การแทนค่าทางคณิตศาสตร์ของฟังก์ชันแสดงให้เห็นอย่างชัดเจนว่าปริมาณหนึ่งกำหนดค่าของอีกปริมาณหนึ่งได้อย่างไร ตามเนื้อผ้า ฟังก์ชันตัวเลขถือเป็นการกำหนดหมายเลขหนึ่งให้กับอีกหมายเลขหนึ่ง ค่าศูนย์ของฟังก์ชันมักจะเป็นค่าของอาร์กิวเมนต์ที่ฟังก์ชันกลายเป็นศูนย์

คำแนะนำ

1. ในการที่จะหาค่าศูนย์ของฟังก์ชัน คุณต้องจัดด้านขวาของฟังก์ชันให้เป็นศูนย์แล้วแก้สมการที่ได้ สมมติว่าคุณได้รับฟังก์ชัน f(x)=x-5

2. ในการค้นหาค่าศูนย์ของฟังก์ชันนี้ ลองหาทางขวาของฟังก์ชันนี้ให้เป็นศูนย์: x-5=0

3. เมื่อแก้สมการนี้แล้ว เราพบว่า x=5 และค่าของอาร์กิวเมนต์นี้จะเป็นศูนย์ของฟังก์ชัน นั่นคือ เมื่อค่าอาร์กิวเมนต์เป็น 5 ฟังก์ชัน f(x) จะกลายเป็นศูนย์

ภายใต้ทัศนียภาพ ฟังก์ชั่นในทางคณิตศาสตร์เราเข้าใจความเชื่อมโยงระหว่างองค์ประกอบของเซต เพื่อให้ถูกต้องมากขึ้น นี่คือ "กฎ" ซึ่งองค์ประกอบทั้งหมดของชุดหนึ่ง (เรียกว่าโดเมนของคำจำกัดความ) เชื่อมโยงกับองค์ประกอบหนึ่งของอีกชุดหนึ่ง (เรียกว่าโดเมนของค่า)

คุณจะต้องการ

• ความรู้เกี่ยวกับพีชคณิตและการทบทวนคณิตศาสตร์

คำแนะนำ

1. ค่านิยม ฟังก์ชั่นนี่คือพื้นที่บางส่วนที่ฟังก์ชันสามารถรับค่าได้ สมมติว่าช่วงของค่า ฟังก์ชั่นฉ(x)=|x| จาก 0 ถึงอนันต์ เพื่อที่จะค้นพบ ความหมาย ฟังก์ชั่นเมื่อถึงจุดหนึ่งคุณจะต้องแทนที่ข้อโต้แย้ง ฟังก์ชั่นเทียบเท่ากับตัวเลข ผลลัพธ์ที่ได้จะเป็นตัวเลข ความหมายม ฟังก์ชั่น. ปล่อยให้ฟังก์ชัน f(x)=|x| – 10 + 4x มาหาคำตอบกัน ความหมาย ฟังก์ชั่นที่จุด x=-2 ลองแทนที่ x ด้วยตัวเลข -2: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16 นั่นคือ ความหมาย ฟังก์ชั่นที่จุด -2 เท่ากับ -16

บันทึก!
ก่อนที่จะค้นหาค่าของฟังก์ชัน ณ จุดหนึ่ง ตรวจสอบให้แน่ใจว่าค่านั้นอยู่ภายในโดเมนของฟังก์ชัน

คำแนะนำที่เป็นประโยชน์
วิธีการที่คล้ายกันทำให้สามารถค้นพบความหมายของฟังก์ชันของอาร์กิวเมนต์ต่างๆ ได้ ข้อแตกต่างก็คือแทนที่จะใช้ตัวเลขตัวเดียว คุณจะต้องแทนที่หลายตัว - ตามจำนวนอาร์กิวเมนต์ของฟังก์ชัน

ฟังก์ชันนี้แสดงถึงการเชื่อมต่อที่สร้างขึ้นระหว่างตัวแปร y และตัวแปร x ยิ่งกว่านั้นค่าทั้งหมดของ x ที่เรียกว่าอาร์กิวเมนต์นั้นสอดคล้องกับค่าพิเศษของ y - ฟังก์ชัน ในรูปแบบกราฟิก ฟังก์ชันจะแสดงบนระบบพิกัดคาร์ทีเซียนในรูปแบบของกราฟ จุดตัดกันของกราฟกับแกน abscissa ซึ่งมีการลงจุดอาร์กิวเมนต์ x เรียกว่าศูนย์ของฟังก์ชัน การค้นหาศูนย์ที่ยอมรับได้ถือเป็นภารกิจหนึ่งในการค้นหาฟังก์ชันที่กำหนด ในกรณีนี้ค่าที่อนุญาตทั้งหมดของตัวแปรอิสระ x ที่สร้างโดเมนของคำจำกัดความของฟังก์ชัน (DOF) จะถูกนำมาพิจารณาด้วย

คำแนะนำ

1. ศูนย์ของฟังก์ชันคือค่าของอาร์กิวเมนต์ x ซึ่งค่าของฟังก์ชันเท่ากับศูนย์ อย่างไรก็ตาม เฉพาะข้อโต้แย้งที่อยู่ในขอบเขตของคำจำกัดความของฟังก์ชันที่กำลังศึกษาเท่านั้นที่สามารถเป็นศูนย์ได้ นั่นคือมีค่ามากมายที่ฟังก์ชัน f(x) มีประโยชน์

2. เขียนฟังก์ชันที่กำหนดและจัดให้เป็นศูนย์ เช่น f(x) = 2x?+5x+2 = 0 แก้สมการผลลัพธ์และหารากที่แท้จริงของมัน รากของสมการกำลังสองถูกคำนวณโดยมีส่วนช่วยในการค้นหาจำแนก 2x?+5x+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;x1 = (-b+?D)/2*a = (-5+3)/2*2 = -0.5;x2 = (-b-?D)/2*a = (-5-3)/2*2 = -2 ดังนั้น ในกรณีนี้ จะได้รากสองอันของสมการกำลังสองซึ่งสอดคล้องกับ อาร์กิวเมนต์ของฟังก์ชันเริ่มต้น f(x)

3. ตรวจสอบค่า x ที่ตรวจพบทั้งหมดว่าเป็นของโดเมนคำจำกัดความของฟังก์ชันที่กำหนด ค้นหา OOF เพื่อดำเนินการนี้ ตรวจสอบนิพจน์เริ่มต้นว่ามีรากคู่ของรูปแบบหรือไม่ f (x) สำหรับการมีอยู่ของเศษส่วนในฟังก์ชันโดยมีอาร์กิวเมนต์ในตัวส่วน สำหรับการมีอยู่ของลอการิทึมหรือตรีโกณมิติ การแสดงออก

4. เมื่อพิจารณาฟังก์ชันที่มีนิพจน์ภายใต้รากของระดับคู่ ให้ใช้โดเมนของคำจำกัดความของอาร์กิวเมนต์ทั้งหมด x ซึ่งค่าที่ไม่เปลี่ยนนิพจน์รากให้เป็นจำนวนลบ (ตรงกันข้ามฟังก์ชันทำ ไม่สมเหตุสมผล) ตรวจสอบว่าค่าศูนย์ที่ตรวจพบของฟังก์ชันอยู่ในช่วงค่า x ที่ยอมรับได้หรือไม่

5. ตัวส่วนของเศษส่วนไม่สามารถเป็นศูนย์ได้ ดังนั้น ให้แยกอาร์กิวเมนต์ x ที่นำไปสู่ผลลัพธ์ดังกล่าวออก สำหรับปริมาณลอการิทึมควรพิจารณาเฉพาะค่าของอาร์กิวเมนต์ที่นิพจน์มีค่ามากกว่าศูนย์ ค่าศูนย์ของฟังก์ชันที่เปลี่ยนนิพจน์ย่อยลอการิทึมให้เป็นศูนย์หรือจำนวนลบจะต้องละทิ้งจากผลลัพธ์สุดท้าย

บันทึก!
เมื่อค้นหารากของสมการ อาจมีรากเพิ่มเติมปรากฏขึ้น ง่ายต่อการตรวจสอบ: เพียงแทนที่ค่าผลลัพธ์ของอาร์กิวเมนต์ลงในฟังก์ชัน และตรวจสอบให้แน่ใจว่าฟังก์ชันเปลี่ยนเป็นศูนย์หรือไม่

คำแนะนำที่เป็นประโยชน์
ในบางครั้งฟังก์ชันจะไม่แสดงอย่างชัดเจนผ่านการโต้แย้ง ดังนั้นจึงเป็นเรื่องง่ายที่จะรู้ว่าฟังก์ชันนี้คืออะไร ตัวอย่างนี้คือสมการของวงกลม

ค่าอาร์กิวเมนต์ z ที่ที่ ฉ(z) ไปที่ศูนย์ที่เรียกว่า จุดศูนย์, เช่น. ถ้า ฉ(ก) = 0 ดังนั้น เอ - จุดศูนย์.

Def.จุด กเรียกว่า ลำดับศูนย์n , ถ้า FKP สามารถแสดงได้ในรูปแบบ ฉ(z) = , โดยที่
ฟังก์ชั่นการวิเคราะห์และ
0.

ในกรณีนี้ในการขยายฟังก์ชันชุดเทย์เลอร์ (43) ครั้งแรก n ค่าสัมประสิทธิ์เป็นศูนย์

= =

ฯลฯ กำหนดลำดับของศูนย์สำหรับ
และ (1 –cos z) ที่ z = 0

=
=

ลำดับที่ 1 เป็นศูนย์

1 – คอส z =
=

ลำดับที่ 2 เป็นศูนย์

Def.จุด z =
เรียกว่า ชี้ไปที่อนันต์และ ศูนย์ฟังก์ชั่น ฉ(z), ถ้า ฉ(
) = 0 ฟังก์ชันดังกล่าวสามารถขยายเป็นอนุกรมที่มีกำลังเป็นลบได้ z : ฉ(z) =
. ถ้า อันดับแรก n สัมประสิทธิ์เท่ากับศูนย์ แล้วเราก็มาถึง ลำดับศูนย์ n ณ จุดที่ไม่มีที่สิ้นสุด: ฉ(z) = z - n
.

จุดเอกพจน์ที่แยกได้แบ่งออกเป็น: ก) จุดเอกพจน์ที่ถอดออกได้; ข) เสาของการสั่งซื้อn; วี) จุดเอกพจน์โดยพื้นฐานแล้ว.

จุด กเรียกว่า จุดเอกพจน์ที่ถอดออกได้ฟังก์ชั่น ฉ(z) ถ้าที่ z
ก ลิม ฉ(z) = กับ -หมายเลขสุดท้าย .

จุด กเรียกว่า เสาแห่งการสั่งซื้อn (n 1) ฟังก์ชั่น ฉ(z) ถ้าเป็นฟังก์ชันผกผัน
= 1/ ฉ(z) ไม่มีลำดับ nตรงจุด ก.ฟังก์ชันดังกล่าวสามารถแสดงเป็นได้เสมอ ฉ(z) =
, ที่ไหน
- ฟังก์ชั่นการวิเคราะห์และ
.

จุด กเรียกว่า โดยพื้นฐานแล้วเป็นจุดพิเศษฟังก์ชั่น ฉ(z) ถ้าอยู่ที่ z
ก ลิม ฉ(z) ไม่ได้อยู่.

ซีรีส์โลรองต์

ให้เราพิจารณากรณีของขอบเขตวงแหวนบรรจบกัน ร < | z 0 – ก| < รมีศูนย์กลางที่จุดหนึ่ง กสำหรับฟังก์ชั่น ฉ(z). ขอแนะนำแวดวงใหม่สองวง ล 1 (ร) และ ล 2 (ร) ใกล้ขอบวงแหวนมีจุด z 0 ระหว่างพวกเขา มาตัดวงแหวนกันเถอะ เชื่อมต่อวงกลมตามขอบของการตัด ย้ายไปยังส่วนที่เชื่อมต่อแบบเรียบง่ายและเข้า

สูตรอินทิกรัลของ Cauchy (39) เราได้อินทิกรัลสองตัวเหนือตัวแปร z

ฉ(z 0) =
+
, (42)

โดยที่การบูรณาการดำเนินไปในทิศทางตรงกันข้าม

สำหรับอินทิกรัลโอเวอร์ ลตรงตามเงื่อนไข 1 ข้อ | z 0 – ก | > | z – ก | และสำหรับอินทิกรัลส่วนเหนือ ล 2 เงื่อนไขผกผัน | z 0 – ก | < | z – ก |. ดังนั้นปัจจัย 1/( z – z 0) ขยายออกเป็นอนุกรม (a) ในอินทิกรัลส่วนเหนือ ล 2 และอยู่ในอนุกรม (b) ในอินทิกรัลส่วนเหนือ ล 1. เป็นผลให้เราได้รับการขยายตัว ฉ(z) ในบริเวณวงแหวนใน ซีรีส์โลรองต์ด้วยพลังบวกและพลังลบ ( z 0 – ก)

ฉ(z 0) =
ก n (z 0 -ก) n (43)

ที่ไหน ก n =
=
;ก -n =

การขยายตัวด้วยพลังบวก (z 0 - ก) เรียกว่า ส่วนที่ถูกต้องซีรีส์ Laurent (ซีรีส์เทย์เลอร์) และการขยายตัวของพลังเชิงลบเรียกว่า ส่วนสำคัญซีรีส์โลรองต์.

ถ้าอยู่ในวงกลม. ล 1 ไม่มีจุดเอกพจน์และฟังก์ชันเป็นแบบวิเคราะห์ จากนั้นใน (44) อินทิกรัลแรกเท่ากับศูนย์ตามทฤษฎีบทของ Cauchy และมีเพียงส่วนที่ถูกต้องเท่านั้นที่เหลืออยู่ในการขยายฟังก์ชัน พลังเชิงลบในการขยาย (45) จะปรากฏเฉพาะเมื่อมีการละเมิดการวิเคราะห์ภายในวงกลมด้านในและทำหน้าที่อธิบายฟังก์ชันใกล้กับจุดเอกพจน์ที่แยกออกจากกัน

เพื่อสร้างซีรีส์ Laurent (45) สำหรับ ฉ(z) คุณสามารถคำนวณค่าสัมประสิทธิ์การขยายตัวโดยใช้สูตรทั่วไป หรือใช้การขยายฟังก์ชันพื้นฐานที่รวมอยู่ในนั้น ฉ(z).

จำนวนเทอม ( n) ของส่วนหลักของซีรี่ส์ Laurent ขึ้นอยู่กับประเภทของจุดเอกพจน์: จุดเอกพจน์ที่ถอดออกได้ (n = 0) ; จุดเอกพจน์โดยพื้นฐานแล้ว (n
); เสาn- ว้าว สั่งเลย(n - หมายเลขสุดท้าย)

และสำหรับ ฉ(z) = จุด z = 0 จุดเอกพจน์ที่ถอดออกได้เพราะ ไม่มีส่วนหลัก ฉ(z) = (z -
) = 1 -

ข) สำหรับ ฉ(z) = จุด z = 0 - เสาลำดับที่ 1

ฉ(z) = (z -
) = -

ค) สำหรับ ฉ(z) = จ 1 / zจุด z = 0 - จุดเอกพจน์โดยพื้นฐานแล้ว

ฉ(z) = จ 1 / z =

ถ้า ฉ(z) มีการวิเคราะห์ในโดเมน ดียกเว้น มจุดเอกพจน์ที่แยกออกจากกัน และ | z 1 | < |z 2 | < . . . < |z ม| แล้วเมื่อขยายฟังก์ชันเป็นกำลัง zเครื่องบินทั้งหมดถูกแบ่งออกเป็น ม+ 1 วง | z ฉัน | < | z | < | z ฉัน+ 1 | และซีรีส์ Laurent ก็มี ประเภทที่แตกต่างกันสำหรับแต่ละแหวน เมื่อขยายอำนาจ ( z – z ฉัน ) ขอบเขตของการบรรจบกันของซีรีส์ Laurent คือวงกลม | z – z ฉัน | < ร, ที่ไหน ร – ระยะทางไปยังจุดเอกพจน์ที่ใกล้ที่สุด

ฯลฯ มาขยายฟังก์ชันกันดีกว่า ฉ(z) =ในซีรีส์ Laurent ในเรื่องพลัง zและ ( z - 1).

สารละลาย. เรามาแสดงฟังก์ชันในรูปแบบกัน ฉ(z) = - z 2 . เราใช้สูตรสำหรับผลรวมของความก้าวหน้าทางเรขาคณิต
. ในวงกลม |z|< 1 ряд сходится и ฉ(z) = - z 2 (1 + z + z 2 + z 3 + z 4 + . . .) = - z 2 - z 3 - z 4 - . . . , เช่น. การสลายตัวประกอบด้วยเท่านั้น ถูกต้องส่วนหนึ่ง. ให้เราย้ายไปที่บริเวณด้านนอกของวงกลม |z| > 1. เรามาแสดงฟังก์ชันในรูปแบบกัน
โดยที่ 1/| z| < 1, и получим разложение ฉ(z) = z
=z + 1 +

เพราะ , การขยายฟังก์ชันของกำลัง ( z - 1) มีรูปแบบ ฉ(z) = (z - 1) -1 + 2 + (z - 1) สำหรับทุกคน
1.

ฯลฯ ขยายฟังก์ชันออกเป็นซีรีส์ Laurent ฉ(z) =
: ก) ตามองศา zอยู่ในวงกลม | z| < 1; b) по степеням z แหวน 1< |z| < 3 ; c) по степеням (z – 2) วิธีแก้ปัญหา ลองแยกฟังก์ชันออกเป็นเศษส่วนอย่างง่ายกัน
= =+=
. จากเงื่อนไข z =1
ก = -1/2 , z =3
บี = ½.

ก) ฉ(z) = ½ [
] = ½ [
-(1/3)
] ด้วย | z|< 1.

ข) ฉ(z) = - ½ [
+
] = - (
) ที่ 1< |z| < 3.

กับ) ฉ(z) = ½ [
]= - ½ [
] =

= - ½ = -
ด้วย |2 - z| < 1

เป็นวงกลมรัศมี 1 มีศูนย์กลางอยู่ที่ z = 2 .

ในบางกรณี อนุกรมกำลังสามารถลดลงเหลือชุดของความก้าวหน้าทางเรขาคณิตได้ และหลังจากนั้น จึงง่ายต่อการกำหนดขอบเขตของการบรรจบกันของอนุกรมกำลัง

ฯลฯ ตรวจสอบการบรรจบกันของซีรีส์

. . . + + + + 1 + () + () 2 + () 3 + . . .

สารละลาย. นี่คือผลรวมของความก้าวหน้าทางเรขาคณิตทั้งสองด้วย ถาม 1 = , ถาม 2 = () . จากเงื่อนไขของการบรรจบกันเป็นไปตามนั้น < 1 , < 1 или |z| > 1 , |z| < 2 , т.е. область сходимости ряда кольцо 1 < |z| < 2 .

ฟังก์ชันศูนย์คืออะไร? คำตอบนั้นค่อนข้างง่าย - นี่คือคำศัพท์ทางคณิตศาสตร์ซึ่งหมายถึงโดเมนของคำจำกัดความของฟังก์ชันที่กำหนดซึ่งค่าของมันคือศูนย์ เรียกอีกอย่างว่าฟังก์ชันศูนย์ วิธีที่ง่ายที่สุดในการอธิบายว่าฟังก์ชันศูนย์คืออะไรโดยใช้ตัวอย่างง่ายๆ

ตัวอย่าง

ลองพิจารณาสมการง่ายๆ y=x+3 เนื่องจากศูนย์ของฟังก์ชันคือค่าของอาร์กิวเมนต์ที่ y ได้รับค่าเป็นศูนย์ เราจึงแทนที่ 0 ทางด้านซ้ายของสมการ:

ในกรณีนี้ -3 คือศูนย์ที่ต้องการ สำหรับฟังก์ชันที่กำหนดจะมีเพียงรากเดียวของสมการ แต่ก็ไม่ได้เป็นเช่นนั้นเสมอไป

ลองดูตัวอย่างอื่น:

ลองแทน 0 ทางด้านซ้ายของสมการ ดังตัวอย่างก่อนหน้านี้:

แน่นอนว่าในกรณีนี้จะมีเลขศูนย์สองตัวของฟังก์ชัน: x=3 และ x=-3 หากสมการมีข้อโต้แย้งระดับที่สาม ก็จะมีศูนย์สามตัว สามารถสรุปง่ายๆ ได้ว่าจำนวนรากของพหุนามสอดคล้องกับระดับสูงสุดของอาร์กิวเมนต์ในสมการ อย่างไรก็ตาม ฟังก์ชันหลายอย่าง เช่น y = x 3 เมื่อมองแวบแรกขัดแย้งกับข้อความนี้ ลอจิกและ การใช้ความคิดเบื้องต้นแนะนำว่าฟังก์ชันนี้มีศูนย์เพียงตัวเดียว - ที่จุด x=0 แต่ในความเป็นจริงแล้ว มีสามราก เพียงแต่ทั้งหมดตรงกัน หากคุณแก้สมการในรูปแบบที่ซับซ้อน สิ่งนี้จะชัดเจนขึ้น x=0 ในกรณีนี้ คือรากที่มีหลายหลากเป็น 3 ในตัวอย่างก่อนหน้านี้ ค่าศูนย์ไม่ตรงกัน ดังนั้นพวกมันจึงมีหลายหลากเป็น 1

อัลกอริธึมการกำหนด

จากตัวอย่างที่นำเสนอ คุณสามารถดูวิธีกำหนดค่าศูนย์ของฟังก์ชันได้ อัลกอริทึมจะเหมือนกันเสมอ:

1. เขียนฟังก์ชัน
2. แทน y หรือ f(x)=0
3. แก้สมการผลลัพธ์

ความยากของจุดสุดท้ายขึ้นอยู่กับระดับของการโต้แย้งของสมการ เมื่อแก้สมการระดับสูง สิ่งสำคัญอย่างยิ่งคือต้องจำไว้ว่าจำนวนรากของสมการเท่ากับระดับสูงสุดของอาร์กิวเมนต์ โดยเฉพาะอย่างยิ่งสำหรับสมการตรีโกณมิติ ซึ่งการหารทั้งสองข้างด้วยไซน์หรือโคไซน์จะทำให้สูญเสียราก

สมการระดับใดก็ได้นั้นแก้ได้ง่ายที่สุดโดยใช้วิธีของฮอร์เนอร์ ซึ่งพัฒนาขึ้นมาโดยเฉพาะสำหรับการค้นหาค่าศูนย์ของพหุนามตามอำเภอใจ

ค่าศูนย์ของฟังก์ชันอาจเป็นค่าลบหรือบวก ค่าจริงหรือในระนาบเชิงซ้อน ค่าเอกพจน์หรือค่าทวีคูณ หรืออาจจะไม่มีรากของสมการ ตัวอย่างเช่น ฟังก์ชัน y=8 จะไม่ได้รับค่าศูนย์สำหรับ x ใดๆ เนื่องจากไม่ได้ขึ้นอยู่กับตัวแปรนี้

สมการ y=x 2 -16 มีสองราก และทั้งสองอยู่ในระนาบเชิงซ้อน: x 1 =4i, x 2 =-4i

ข้อผิดพลาดทั่วไป

ข้อผิดพลาดทั่วไปที่ทำโดยเด็กนักเรียนที่ยังไม่เข้าใจอย่างถ่องแท้ว่าค่าศูนย์ของฟังก์ชันคืออะไรคือการแทนที่อาร์กิวเมนต์ (x) ด้วยศูนย์ แทนที่จะเป็นค่า (y) ของฟังก์ชัน พวกเขาแทนที่ x=0 ลงในสมการอย่างมั่นใจ และจากสิ่งนี้ จงหา y แต่นี่เป็นแนวทางที่ผิด

ข้อผิดพลาดอีกประการหนึ่ง ดังที่กล่าวไปแล้วคือการลดลงด้วยไซน์หรือโคไซน์ในสมการตรีโกณมิติ ซึ่งเป็นสาเหตุที่ทำให้ฟังก์ชันมีค่าศูนย์ตั้งแต่หนึ่งตัวขึ้นไปหายไป นี่ไม่ได้หมายความว่าจะไม่มีอะไรลดลงในสมการดังกล่าว แต่ในการคำนวณเพิ่มเติมจำเป็นต้องคำนึงถึงปัจจัยที่ "สูญหาย" เหล่านี้ด้วย

การแสดงกราฟิก

คุณสามารถเข้าใจได้ว่าค่าศูนย์ของฟังก์ชันกำลังทำอะไรอยู่โดยใช้โปรแกรมทางคณิตศาสตร์ เช่น Maple คุณสามารถสร้างกราฟได้โดยระบุจำนวนจุดที่ต้องการและมาตราส่วนที่ต้องการ จุดที่กราฟตัดกับแกน OX คือศูนย์ที่ต้องการ นี่คือหนึ่งในที่สุด วิธีที่รวดเร็วการหารากของพหุนาม โดยเฉพาะอย่างยิ่งถ้าลำดับของมันสูงกว่าอันดับสาม ดังนั้นหากมีความจำเป็นต้องคำนวณทางคณิตศาสตร์เป็นประจำการค้นหารากของพหุนามขององศาที่ต้องการสร้างกราฟเมเปิ้ลหรือโปรแกรมที่คล้ายกันจะขาดไม่ได้ในการดำเนินการและตรวจสอบการคำนวณ