Güvenlik bilgi portalı. Skaler ölçümler için Kalman filtresi Kalman filtresi

Wiener filtreleri, süreçlerin veya süreçlerin bir bütün olarak bölümlerinin (blok işleme) işlenmesi için en uygunudur. Sıralı işleme, gözlem süreci sırasında filtre girişinde alınan bilgileri dikkate alarak, her saat döngüsünde sinyalin güncel bir değerlendirmesini gerektirir.

Wiener filtrelemeyle her yeni sinyal örneği, tüm filtre ağırlık katsayılarının yeniden hesaplanmasını gerektirecektir. Şu anda, gelen filtrelerin kullanıldığı uyarlanabilir filtreler yeni bilgi Daha önce yapılmış bir sinyal değerlendirmesinin (radarda hedef takibi, kontrolde otomatik kontrol sistemleri vb.) sürekli olarak ayarlanması için kullanılır. Kalman filtresi olarak bilinen uyarlanabilir özyinelemeli filtreler özellikle ilgi çekicidir.

Bu filtreler, otomatik düzenleme ve kontrol sistemlerinde kontrol döngülerinde yaygın olarak kullanılmaktadır. Çalışmalarını durum alanı olarak tanımlamak için kullanılan özel terminolojinin de gösterdiği gibi, geldikleri yer burasıdır.

Sinirsel hesaplama pratiğinde çözülmesi gereken temel problemlerden biri, sinir ağlarının eğitimi için hızlı ve güvenilir algoritmaların elde edilmesidir. Bu bağlamda olabilir faydalı kullanım doğrusal filtre eğitim algoritmasının geri bildirim döngüsünde. Öğrenme algoritmaları doğası gereği yinelemeli olduğundan, böyle bir filtrenin sıralı yinelemeli bir tahmin edici olması gerekir.

Parametre Tahmin Problemi

İstatistiksel çözümler teorisindeki pratik açıdan büyük öneme sahip problemlerden biri, aşağıdaki şekilde formüle edilen sistemlerin durum vektörlerini ve parametrelerini tahmin etme problemidir. Doğrudan ölçülemeyen $X$ vektör parametresinin değerini tahmin etmenin gerekli olduğunu varsayalım. Bunun yerine, $X$'a bağlı olarak başka bir $Z$ parametresi ölçülür. Tahmin görevi şu soruyu cevaplamaktır: $Z$'ı bilerek $X$ hakkında ne söylenebilir? Genel olarak, $X$ vektörünün optimal tahminine yönelik prosedür, tahminin kalitesi için benimsenen kritere bağlıdır.

Örneğin, parametre tahmini problemine yönelik Bayesian yaklaşımı, tahmin edilen parametrenin olasılıksal özellikleri hakkında tam bir önsel bilgi gerektirir ki bu genellikle imkansızdır. Bu durumlarda, önemli ölçüde daha az ön bilgi gerektiren en küçük kareler yöntemine (LSM) başvuruyorlar.

Gözlem vektörü $Z$'nin doğrusal bir model aracılığıyla parametre tahmin vektörü $X$ ile ilişkili olduğu ve gözlemin tahmin edilen parametre ile ilişkisiz gürültü $V$ içerdiği durum için en küçük kareler uygulamasını ele alalım:

$Z = HX + V$, (1)

burada $H$ gözlemlenen miktarlar ile tahmin edilen parametreler arasındaki ilişkiyi açıklayan dönüşüm matrisidir.

Karesel hatayı en aza indiren $X$ tahmini şu şekilde yazılır:

$X_(ots)=(H^TR_V^(-1)H)^(-1)H^TR_V^(-1)Z$, (2)

$V$ gürültüsünün ilişkisiz olmasına izin verin, bu durumda $R_V$ matrisi basitçe birim matristir ve tahmin denklemi daha basit hale gelir:

$X_(ots)=(H^TH)^(-1)H^TZ$, (3)

Matris biçiminde yazmak çok fazla kağıt tasarrufu sağlar, ancak bazıları için alışılmadık bir durum olabilir. Yu. M. Korshunov'un "Sibernetiğin Matematiksel Temelleri" monografisinden alınan aşağıdaki örnek tüm bunları göstermektedir.
Aşağıdaki elektrik devresi vardır:

Bu durumda gözlemlenen miktarlar, $A_1 ​​​​= 1 A, A_2 = 2 A, V = 20 B$ cihaz okumalarıdır.

Ayrıca direncin $R = 5$ Ohm olduğu da biliniyor. Minimum ortalama karesel hata kriteri açısından $I_1$ ve $I_2$ akımlarının değerlerinin mümkün olan en iyi şekilde tahmin edilmesi gerekmektedir. Burada en önemli şey, gözlemlenen miktarlar (cihaz okumaları) ile tahmin edilen parametreler arasında bir ilişki olmasıdır. Ve bu bilgiler dışarıdan getiriliyor.

Bu durumda bunlar, filtreleme durumunda (daha sonra tartışılacaktır) Kirchhoff yasalarıdır - mevcut değerin öncekilere bağımlılığını varsayan bir zaman serisinin otoregresif bir modeli.

Dolayısıyla, istatistiksel çözüm teorisiyle hiçbir şekilde bağlantılı olmayan Kirchhoff yasalarının bilgisi, gözlemlenen değerler ile tahmin edilen parametreler arasında bir bağlantı kurmamıza olanak tanır (elektrik mühendisliği eğitimi almış olanlar kontrol edebilir, geri kalanı sahip olacaktır). onların sözüne güvenmek gerekirse):

$$z_1 = A_1 = I_1 + \xi_1 = 1$$

$$z_2 = A_2 = I_1 + I_2 + \xi_2 = 2$$

$$z_2 = V/R = I_1 + 2 * I_2 + \xi_3 = 4$$

Bu vektör biçimindedir:

$$\begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) \begin(vmatrix) I_1\ \ I_2 \end(vmatrix) + \begin(vmatrix) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrix)$$

Veya $Z = HX + V$, burada

$$Z= \begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1\\ 2\\ 4 \end(vmatrix) ; H= \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) ; X= \begin(vmatrix) I_1\\ I_2 \end(vmatrix) ; V= \begin(vmatrix) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrix)$$

Gürültü değerlerinin birbiriyle ilişkisiz olduğu göz önüne alındığında, formül 3'e göre en küçük kareler yöntemini kullanarak I 1 ve I 2 tahminini bulacağız:

$H^TH= \begin(vmatrix) 1 & 1& 1\\ 0 & 1& 2 \end(vmatrix) \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) = \ begin(vmatrix) 3 & 3\\ 3 & 5 \end(vmatrix) ; (H^TH)^(-1)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) $;

$H^TZ= \begin(vmatrix) 1 & 1& 1\\ 0 & 1& 2 \end(vmatrix) \begin(vmatrix) 1 \\ 2\\ 4 \end(vmatrix) = \begin(vmatrix) 7\ \ 10 \end(vmatrix) ; X(ots)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) \begin(vmatrix) 7\\ 10 \end(vmatrix) = \frac (1)(6) \begin(vmatrix) 5\\ 9 \end(vmatrix)$;

Yani $I_1 = 5/6 = 0,833 A$; $I_2 = 9/6 = 1,5 A$.

Filtreleme görevi

Sabit değerlere sahip parametreleri tahmin etme probleminin aksine, filtreleme problemi tahmin süreçlerini, yani gürültü tarafından bozulan ve dolayısıyla doğrudan ölçüme erişilemeyen zamanla değişen bir sinyalin mevcut tahminlerini bulmayı gerektirir. Genel olarak filtreleme algoritmalarının türü, sinyalin ve gürültünün istatistiksel özelliklerine bağlıdır.

Yararlı sinyalin zamanın yavaşça değişen bir fonksiyonu olduğunu ve girişimin ilişkisiz gürültü olduğunu varsayacağız. Sinyal ve gürültünün olasılıksal özellikleri hakkında ön bilgi eksikliğinden dolayı yine en küçük kareler yöntemini kullanacağız.

İlk olarak, $z_n, z_(n-1),z_(n-2)\dots z_(n-) zaman serisinin mevcut $k$ en son değerlerine dayanarak mevcut $x_n$ değerine ilişkin bir tahmin elde ederiz. (k-1))$. Gözlem modeli parametre tahmin problemindekiyle aynıdır:

$Z$'ın $z_n, z_(n-1),z_(n-2)\dots z_(n-(k-1))$ zaman serisinin gözlemlenen değerlerinden oluşan bir sütun vektörü olduğu açıktır. , $V $ gürültü sütun vektörüdür $\xi _n, \xi _(n-1),\xi_(n-2)\dots \xi _(n-(k-1))$, gerçek sinyali bozar . $H$ ve $X$ sembolleri ne anlama geliyor? Örneğin, gereken tek şey zaman serisinin mevcut değerini tahmin etmekse, $X$ sütun vektöründen ne bahsedebiliriz? Ve dönüşüm matrisi $H$ ile ne kastedildiği genellikle açık değildir.

Tüm bu soruların yanıtı ancak sinyal üretim modeli kavramının dikkate alınmasıyla mümkün olabilir. Yani orijinal sinyalin bir modeline ihtiyaç vardır. Bu anlaşılabilir bir durumdur; sinyalin ve girişimin olasılıksal özellikleri hakkında önceden bilgi olmadığında, yalnızca varsayımlarda bulunulabilir. Buna kahve telvesi üzerine falcılık diyebilirsiniz ancak uzmanlar farklı bir terminolojiyi tercih ediyor. Saç kurutma makinelerinde buna parametrik model denir.

Bu durumda, bu özel modelin parametreleri tahmin edilir. Uygun bir sinyal üretme modeli seçerken herhangi bir analitik fonksiyonun Taylor serisine genişletilebileceğini unutmayın. Taylor serisinin çarpıcı bir özelliği, belirli bir $x=a$ noktasından herhangi bir sonlu $t$ mesafesindeki bir fonksiyonun formunun, fonksiyonun $x=a noktasının sonsuz küçük bir komşuluğundaki davranışı tarafından benzersiz bir şekilde belirlenmesidir. $ (birinci ve daha yüksek dereceli türevlerinden bahsediyoruz).

Dolayısıyla Taylor serisinin varlığı analitik fonksiyonun çok güçlü bağlaşıma sahip bir iç yapıya sahip olduğu anlamına gelir. Örneğin, kendimizi Taylor serisinin üç terimiyle sınırlandırırsak, sinyal üretme modeli şu şekilde görünecektir:

$x_(n-i) = F_(-i)x_n$, (4)

$$X_n= \begin(vmatrix) x_n\\ x"_n\\ x""_n \end(vmatrix) ; F_(-i)= \begin(vmatrix) 1 & -i & i^2/2\\ 0 & 1 & -i\\ 0 & 0 & 1 \end(vmatrix) $$

Yani, formül 4, polinomun belirli bir sırası için (örnekte 2'ye eşittir), zaman dizisindeki sinyalin $n$-th değeri ile $(n-i)$- arasında bir bağlantı kurar. inci Dolayısıyla bu durumda tahmin edilen durum vektörü, tahmin edilen değerin kendisine ek olarak sinyalin birinci ve ikinci türevlerini de içerir.

Otomatik kontrol teorisinde böyle bir filtreye 2. dereceden astatismli filtre adı verilir. Bu durum için dönüşüm matrisi $H$ (mevcut ve önceki $k-1$ örnekleri kullanılarak tahmin edilmiştir) şuna benzer:

$$H= \begin(vmatrix) 1 & -k & k^2/2\\ - & - & -\\ 1 & -2 & 2\\ 1 & -1 & 0,5\\ 1 & 0 & 0 \ bitiş(vmatrix)$$

Tüm bu sayılar, bitişik gözlenen değerler arasındaki zaman aralığının sabit ve 1'e eşit olduğu varsayımıyla Taylor serisinden elde edilmiştir.

Yani yaptığımız varsayımlar altında filtreleme problemi parametre tahmini problemine indirgenmiştir; bu durumda benimsediğimiz sinyal üretim modelinin parametreleri tahmin edilir. Ve $X$ durum vektörünün değerlerinin değerlendirilmesi aynı formül 3 kullanılarak gerçekleştirilir:

$$X_(ots)=(H^TH)^(-1)H^TZ$$

Temel olarak, sinyal üretim sürecinin otoregresif modeline dayalı bir parametrik tahmin süreci uyguladık.

Formül 3 yazılımda kolayca uygulanabilir; bunu yapmak için $H$ matrisini ve $Z$ gözlem sütunu vektörünü doldurmanız gerekir. Bu tür filtrelere denir sonlu hafızalı filtreler, çünkü mevcut $X_(noc)$ tahminini elde etmek için son $k$ gözlemlerini kullanıyorlar. Her yeni gözlem adımında, mevcut gözlem kümesine yenisi eklenir ve eskisi atılır. Tahminlerin elde edildiği bu sürece denir sürgülü pencere.

Büyüyen belleğe sahip filtreler

Sonlu belleğe sahip filtrelerin ana dezavantajı, her yeni gözlemden sonra bellekte saklanan tüm verilerin yeniden hesaplanmasının gerekli olmasıdır. Ayrıca tahminlerin hesaplanması ancak ilk $k$ gözlemlerinin sonuçları toplandıktan sonra başlayabilir. Yani bu filtrelerin geçici işlem süresi uzundur.

Bu dezavantajla mücadele etmek için kalıcı hafızalı bir filtreden kalıcı hafızalı bir filtreye geçmek gerekir. Büyüyen hafıza. Böyle bir filtrede değerlendirmenin yapıldığı gözlemlenen değerlerin sayısı, mevcut gözlemin n sayısıyla eşleşmelidir. Bu, tahmin edilen $X$ vektörünün bileşen sayısına eşit sayıda gözlemden başlayarak tahminler elde etmemizi sağlar. Bu da benimsenen modelin sırasına, yani modelde Taylor serisinden kaç terimin kullanıldığına göre belirlenir.

Bu durumda n arttıkça filtrenin yumuşatma özellikleri iyileşir, yani tahminlerin doğruluğu artar. Ancak bu yaklaşımın doğrudan uygulanması hesaplama maliyetlerinde artışa neden olur. Bu nedenle, büyüyen belleğe sahip filtreler şu şekilde uygulanır: tekrarlayan.

Gerçek şu ki, n zamanına gelindiğinde zaten tüm önceki gözlemler $z_n, z_(n-1), z_(n-2) \dots z_ hakkında bilgi içeren $X_((n-1)ots)$ tahminine sahibiz. (n-(k-1))$. $X_(nots)$ tahmini, $X_((n-1))(\mbox (ots))$ tahmininde saklanan bilgi kullanılarak sonraki $z_n$ gözleminden elde edilir. Bu prosedüre tekrarlayan filtreleme denir ve aşağıdakilerden oluşur:

• $X_((n-1))(\mbox (ots))$ tahminine göre, $i = 1$ için formül 4'ü kullanarak $X_n$ tahminini tahmin edin: $X_(\mbox (notspriori)) = F_1X_( (n-1 )ots)$. Bu önsel bir tahmindir;
• mevcut $z_n$ gözleminin sonuçlarına göre, bu a priori tahmin doğruya, yani a posteriori'ye dönüştürülür;
• bu prosedür $r+1$'dan başlayarak her adımda tekrarlanır; burada $r$, filtrenin sırasıdır.

Son yinelenen filtreleme formülü şuna benzer:

$X_((n-1)oc) = X_(\mbox (nocapriori)) + (H^T_nH_n)^(-1)h^T_0(z_n - h_0 X_(\mbox (nocapriori)))$, (6 )

ikinci dereceden filtremiz için nerede:

Formül 6'ya göre çalışan büyüyen bellek filtresi, Kalman filtresi olarak bilinen filtreleme algoritmasının özel bir durumudur.

Bu formülü pratikte uygularken, içerdiği önsel tahminin formül 4 ile belirlendiğini ve $h_0 X_(\mbox (nocapriori))$ değerinin $X_( vektörünün ilk bileşenini temsil ettiğini hatırlamak gerekir. \mbox (nocapriori))$.

Büyüyen bellek filtresinin önemli bir özelliği vardır. Formül 6'ya bakarsanız, nihai tahmin, tahmin edilen tahmin vektörü ile düzeltme teriminin toplamıdır. Bu düzeltme küçük $n$ için büyüktür ve $n$ arttıkça azalır, $n \rightarrow \infty$'da sıfıra yönelir. Yani n arttıkça filtrenin yumuşatma özellikleri artar ve içine gömülü model hakim olmaya başlar. Ancak gerçek sinyal modele ancak belirli bir dereceye kadar karşılık gelebilir. ayrı alanlar dolayısıyla tahmin doğruluğu bozulur.

Bununla mücadele etmek için belirli bir $n$'dan başlayarak düzeltme süresinin daha da azaltılmasına yasak getiriliyor. Bu, filtre bandını değiştirmeye eşdeğerdir, yani küçük n için filtre daha geniş bant genişliğine sahiptir (daha az eylemsizdir), büyük n için daha eylemsiz hale gelir.

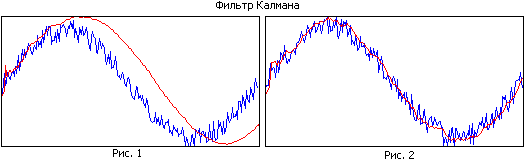
Şekil 1 ile Şekil 2'yi karşılaştırın. İlk şekilde, filtrenin büyük bir hafızası vardır ve iyi bir şekilde yumuşar, ancak dar bant nedeniyle tahmini yörünge gerçek olanın gerisinde kalır. İkinci şekilde, filtre hafızası daha küçüktür, daha kötü şekilde yumuşatır, ancak gerçek yörüngeyi daha iyi takip eder.

Edebiyat

1. Yu.M Korshunov "Sibernetiğin Matematiksel Temelleri"
2. A.V.Balakrishnan "Kalman filtrasyon teorisi"
3. V.N.Fomin "Tekrarlayan tahmin ve uyarlanabilir filtreleme"
4. C.F.N.Cowan, PM "Uyarlanabilir filtreler" ver

Şekil 1

Dolayısıyla aradığımız çift bu düz çizgi üzerinde bir yerde bulunuyor. Tekrar ediyorum, tüm bu seçenekler arasından gerçekte var olan ve 12 sayısını veren çifti herhangi bir ek ipucu bilmeden seçmek imkansızdır. Fakat, Kalman filtresinin icat edildiği durumda bu tür ipuçları mevcut. Rasgele sayılar hakkında önceden bilinen bir şey var. Özellikle, her sayı çiftinin dağılım histogramı burada bilinmektedir. Genellikle aynı rastgele sayıların oluşumunun yeterince uzun süre gözlemlenmesinden sonra elde edilir. Yani, örneğin, deneyimlerden, vakaların %5'inde genellikle x=1, y=8 çiftinin ortaya çıktığı (bu çifti şu şekilde belirtiyoruz: (1,8)), vakaların %2'sinde çiftin ortaya çıktığı bilinmektedir. x=2, y=3 ( 2,3), vakaların %1'inde bir çift (3,1), vakaların %0,024'ünde bir çift (11,1), vb. Tekrar ediyorum, bu histogram verilmiştir tüm çiftler için Toplamları 12'ye ulaşanlar da dahil olmak üzere sayılar. Dolayısıyla toplamı 12'ye ulaşan her çift için, örneğin (1, 11) çiftinin %0,8 oranında göründüğünü, ( 2, 10) çiftinin göründüğünü söyleyebiliriz. – vakaların %1'inde, ikili (3, 9) – vakaların %1,5'inde vb. Böylece, bir çiftin terimlerinin toplamının yüzde kaç durumda 12'ye eşit olduğunu belirlemek için histogramı kullanabiliriz. Örneğin, vakaların %30'unda toplamın 12 verdiğini varsayalım. Geri kalan %70'te ise, kalan çiftler düşer - bunlar (1,8), (2, 3), (3,1), vb. – toplamı 12 dışındaki sayılara karşılık gelenler. Ayrıca, örneğin (7,5) çifti vakaların %27'sinde görünse de, toplamı 12'ye ulaşan tüm diğer çiftler %0,024+%0,8 +1'de görünsün. Vakaların %+%1,5+…=%3'ü. Yani histogramdan toplamı 12'ye ulaşan sayıların vakaların %30'unda göründüğünü öğrendik. Üstelik, eğer bir 12 atılırsa, çoğunlukla (%30'un %27'si) bunun nedeninin (7,5) çifti olduğunu biliyoruz. Yani eğer çoktan Eğer 12 atılırsa, vakaların %90'ında (%30'un %27'si - veya aynı şekilde her 30'un 27'sinde) 12 atmanın nedeninin (7,5) çifti olduğunu söyleyebiliriz. . Çoğu zaman 12'ye eşit bir toplam almanın nedeninin çift (7,5) olduğunu bilerek, büyük olasılıkla şimdi düştüğünü varsaymak mantıklıdır. Tabii ki, aslında 12 sayısının bu özel çiftten oluştuğu hala bir gerçek değil, ancak bir dahaki sefere 12 ile karşılaşırsak ve tekrar (7,5) çiftini varsayarsak, o zaman yaklaşık% 90 oranında olur. vakaların %100'ünde haklı çıkacağız. Ancak (2, 10) çiftini tahmin edersek, vakaların %30'unun yalnızca %1'inde haklı oluruz; bu, (7,5) çiftini tahmin ederken %90'a kıyasla doğru tahminlerin %3,33'üne eşittir. İşte bu, Kalman filtre algoritmasının amacı da bu. Yani Kalman filtresi, toplamın toplamla belirlenmesinde hata yapmayacağını garanti etmez, ancak minimum sayıda hata yapacağını garanti eder (hata olasılığı minimum olacaktır), çünkü sayı çiftlerinin oluşumunun histogramı olan istatistikleri kullanır. Kalman filtreleme algoritmasının sıklıkla olasılık dağılım yoğunluğunu (PDD) kullandığını da vurgulamak gerekir. Ancak buradaki anlamın histogramdaki anlamla aynı olduğunu anlamak gerekir. Ayrıca histogram, PDF temelinde oluşturulmuş bir fonksiyondur ve onun yaklaşımıdır (örneğin bkz.).
Prensip olarak, bu histogramı iki değişkenin bir fonksiyonu olarak, yani xy düzleminin üzerinde belirli bir yüzey şeklinde tasvir edebiliriz. Yüzeyin daha yüksek olduğu yerde karşılık gelen çifti alma olasılığı daha yüksektir. Şekil 2 böyle bir yüzeyi göstermektedir.

İncir. 2

Yukarıda görüldüğü gibi x+y=12 (verme çiftlerinin varyantları toplam 12'dir) doğrusunun yüzey noktaları farklı yüksekliklerde yer alır ve en yüksek yükseklik (7,5) koordinatlı varyant içindir. Ve 12'ye eşit bir toplamla karşılaştığımızda, vakaların %90'ında bu toplamın ortaya çıkmasının nedeni tam olarak (7,5) ikilisidir. Onlar. Toplamın 12 olması koşuluyla, oluşma olasılığı en yüksek olan, toplamı 12 olan bu çifttir.
Böylece Kalman filtresinin arkasındaki fikir burada anlatılmaktadır. Her türlü modifikasyonu bu temelde inşa edilmiştir - tek adımlı, çok adımlı tekrarlayan vb. Kalman filtresinin daha derinlemesine incelenmesi için şu kitabı tavsiye ederim: Van Trees G. Tespit, tahmin ve modülasyon teorisi.

not: Matematik kavramlarının “parmaklarda” dedikleri gibi açıklamalarıyla ilgilenenler için bu kitabı ve özellikle “Matematik” bölümündeki bölümleri önerebiliriz (kitabın kendisini veya içindeki bölümleri satın alabilirsiniz). ).

Entegre sistemlerin modern gelişmelerinde Kalman filtresinin kullanımına ilişkin bir çalışma navigasyon sistemleri. Bir inşaat örneği veriliyor ve analiz ediliyor matematiksel modelİnsansız hava araçlarının koordinatlarını belirleme doğruluğunu artırmak için genişletilmiş bir Kalman filtresi kullanan. Kısmi bir filtre dikkate alınır. Yapılmış kısa inceleme bilimsel çalışmalar Navigasyon sistemlerinin güvenilirliğini ve hata toleransını geliştirmek için bu filtreyi kullanır. Bu makale, Kalman filtresinin İHA konum sistemlerinde kullanımının birçok modern gelişmede uygulandığı sonucuna varmamızı sağlıyor. Bu kullanımın, özellikle standart uydu navigasyon sistemlerinin arızalanması durumunda, doğruluğun arttırılmasında somut sonuçlar sağlayan çok sayıda varyasyonu ve yönü vardır. Bu teknolojinin, çeşitli uçaklar için doğru ve hataya dayanıklı navigasyon sistemlerinin geliştirilmesiyle ilgili çeşitli bilimsel alanlara etkisindeki ana faktör budur.

Kalman filtresi

navigasyon

insansız hava aracı (İHA)

1. Makarenko G.K., Aleshechkin A.M. Uydu radyo navigasyon sistemlerinden gelen sinyalleri kullanarak bir nesnenin koordinatlarını belirlerken bir filtreleme algoritmasının incelenmesi // TUSUR Raporları. – 2012. – Sayı 2 (26). – s. 15-18.

2. Bar-Shalom Y., Li X.R., Kirubarajan T. Uygulamalarla Tahmin

İzleme ve Navigasyona // Teori Algoritmalar ve Yazılım. – 2001. – Cilt. 3. – S.10-20.

3. Bassem I.S. İnsansız Hava Araçlarının (İHA) Görüş Tabanlı Navigasyonu (VBN) // CALGARY ÜNİVERSİTESİ. – 2012. – Cilt. 1. – S. 100-127.

4. Conte G., Doherty P. Havadan Görüntü Eşleştirmeye Dayalı Entegre Bir İHA Navigasyon Sistemi // Havacılık ve Uzay Konferansı. – 2008. –Cilt. 1. – S.3142-3151.

5. Guoqiang M., Drake S., Anderson B. İha lokalizasyonu için genişletilmiş bir Kalman filtresinin tasarımı // Bilgi, Karar ve Kontrolde. – 2007. – Cilt. 7. – S. 224–229.

6. Küçük İnsansız Hava Araçlarını Kullanarak Hedef Lokalizasyonu için Ponda S.S Yörünge Optimizasyonu // Massachusetts Teknoloji Enstitüsü. – 2008. – Cilt. 1. – S.64-70.

7. Wang J., Garrat M., Lambert A. İnsansız hava araçlarında gezinmek için gps/ins/vision sensörlerinin entegrasyonu // IAPRS&SIS. – 2008. – Cilt. 37. – S.963-969.

İnsansız hava araçlarının (İHA) modern navigasyonunun acil görevlerinden biri, koordinat belirleme doğruluğunun arttırılması görevidir. Bu sorun kullanılarak çözülür Çeşitli seçenekler Navigasyon sistemlerinin entegrasyonu. Biri modern seçenekler entegrasyon, GPS/Glonass navigasyonunun, eksik ve gürültülü ölçümler kullanarak doğruluğu yinelemeli olarak değerlendiren Genişletilmiş Kalman filtresiyle birleşimidir. İÇİNDE şu an Genişletilmiş Kalman filtresinin çeşitli varyasyonları mevcuttur ve çok sayıda durum değişkeni dahil olmak üzere geliştirilmektedir. Bu çalışmamızda modern gelişmelerde kullanımının ne kadar etkili olabileceğini göstereceğiz. Böyle bir filtrenin karakteristik gösterimlerinden birini ele alalım.

Matematiksel bir model oluşturmak

İÇİNDE bu örnekte sadece İHA'nın yatay düzlemdeki hareketinden bahsedeceğiz, aksi takdirde 2d lokalizasyon problemini ele alacağız. Bizim durumumuzda bu, pratikte karşılaşılan birçok durumda İHA'nın yaklaşık olarak aynı yükseklikte kalabileceği gerçeğiyle doğrulanmaktadır. Bu varsayım, uçak dinamiği simülasyonlarını basitleştirmek için yaygın olarak kullanılır. İHA'nın dinamik modeli aşağıdaki denklem sistemiyle belirlenir:

Burada () İHA'nın yatay düzlemdeki zamana bağlı koordinatları, İHA'nın yönü, İHA'nın açısal hızı ve İHA'nın yer hızı fonksiyonlarıdır ve sabit kabul edilecektir. Bilinen kovaryanslarla karşılıklı olarak bağımsızdırlar ve sırasıyla ve eşittir ve rüzgar, pilot manevraları vb. nedeniyle İHA ivmesindeki değişiklikleri modellemek için kullanılır. Değerler ve değerleri, İHA'nın maksimum açısal hızından ve İHA'nın doğrusal hızındaki değişikliklerin deneysel değerlerinden, - Kronecker sembolünden türetilmiştir.

Bu denklem sistemi, modeldeki doğrusal olmama ve gürültünün varlığı nedeniyle yaklaşık olacaktır. Bu durumda en basit yaklaşım yöntemi Euler yaklaşım yöntemidir. İHA'nın dinamik tahrik sisteminin ayrı bir modeli aşağıda gösterilmektedir.

sürekli durum vektörünün değerine yaklaşmaya izin veren ayrık bir Kalman filtresi durum vektörü. ∆ - k ve k+1 ölçümleri arasındaki zaman aralığı. () ve (), sıfır ortalamalı beyaz Gauss gürültü değerlerinin dizileridir. İlk dizi için kovaryans matrisi:

Benzer şekilde ikinci sıra için:

Sistem (2) denklemlerinde uygun ikameleri yaptıktan sonra şunu elde ederiz:

Diziler ve birbirlerinden bağımsızdırlar. Bunlar aynı zamanda kovaryans matrisleri ve sırasıyla sıfır ortalamalı beyaz Gauss gürültü dizileridir. Bu formun avantajı, her ölçüm arasında ayrı gürültüdeki değişimi göstermesidir. Sonuç olarak aşağıdaki ayrık dinamik modeli elde ederiz:

(3)

Denklem:

= + , (4)

burada x ve y, İHA'nın k zamanındaki koordinatlarıdır ve hatayı ayarlamak için kullanılan, sıfır ortalama değerli rastgele parametrelerin Gauss dizisidir. Bu dizinin () ve ()'den bağımsız olduğu varsayılmaktadır.

İfadeler (3) ve (4), İHA'nın konumunu tahmin etmek için temel oluşturur; k-e koordinatları genişletilmiş Kalman filtresi kullanılarak elde edilmiştir. Navigasyon sistemlerinin başarısızlığının modellenmesi bu tip filtre önemli verimliliğini gösterir.

Daha fazla netlik sağlamak için küçük, basit bir örnek verelim. Bazı İHA'ların sabit bir ivmeyle eşit hızla uçmasına izin verin a.

Burada x, İHA'nın t zamanındaki koordinatıdır ve δ, bir rastgele değişkendir.

Bir uçağın konumu hakkında veri alan bir GPS sensörümüz olduğunu varsayalım. Bu sürecin modellenmesi sonucunu MATLAB yazılım paketinde sunalım.

Pirinç. 1. Kalman filtresi kullanarak sensör okumalarının filtrelenmesi

İncirde. Şekil 1, Kalman filtrelemesinin kullanımının ne kadar etkili olabileceğini göstermektedir.

Ancak gerçek durumlarda sinyaller genellikle doğrusal olmayan dinamiklere ve anormal gürültüye sahiptir. Bu gibi durumlarda genişletilmiş Kalman filtresi kullanılır. Gürültü varyansları çok büyük değilse (yani doğrusal yaklaşım yeterliyse), genişletilmiş Kalman filtresinin kullanılması soruna yüksek doğrulukla çözüm sağlar. Ancak gürültünün Gaussian olmaması durumunda genişletilmiş Kalman filtresi kullanılamaz. Bu durumda genellikle Markov zincirleriyle Monte Carlo yöntemlerine dayalı sayısal integral yöntemleri kullanan kısmi bir filtre kullanılır.

Kısmi filtre

Kısmi bir filtre olan genişletilmiş Kalman filtresinin fikirlerini geliştiren algoritmalardan birini hayal edelim. Kısmi filtreleme, sürecin olasılık dağılımını temsil eden bir dizi parçacık üzerinde Monte Carlo havuzlaması yapılarak çalışan, optimal olmayan bir filtreleme tekniğidir. Burada parçacık, tahmin edilen parametrenin önceki dağılımından alınan bir elementtir. Kısmi filtrenin temel fikri şudur: çok sayıda parçacıklar dağılımın bir tahminini temsil etmek için kullanılabilir. Kullanılan parçacıkların sayısı ne kadar büyük olursa, parçacık seti önceki dağılımı o kadar doğru bir şekilde temsil edecektir. Parçacık filtresi, tahmin etmek istediğimiz parametrelerin önceki dağılımından N tane parçacığın yerleştirilmesiyle başlatılır. Filtreleme algoritması bu parçacıkların içinden geçirilmesini içerir. özel sistem ve ardından bu parçacıkların ölçülmesinden elde edilen bilgileri kullanarak tartım. Ortaya çıkan parçacıklar ve bunlarla ilişkili kütleler, tahmin sürecinin sonsal dağılımını temsil eder. Döngü her yeni ölçüm için tekrarlanır ve parçacık ağırlıkları sonraki dağılımı temsil edecek şekilde güncellenir. Geleneksel parçacık filtreleme yaklaşımındaki ana sorunlardan biri, yaklaşımın tipik olarak birkaç parçacığın çok büyük ağırlıklara sahip olmasıyla sonuçlanması, diğerlerinin çoğunun ise çok az ağırlığa sahip olmasıyla sonuçlanmasıdır. Bu, filtrelemenin kararsız olmasına yol açar. Bu sorun, eski parçacıklardan oluşan bir dağılımdan N yeni parçacığın alındığı bir örnekleme hızı getirilerek çözülebilir. Tahmin sonucu, bir parçacık kümesinin ortalama değerinin bir örneğinin alınmasıyla elde edilir. Birden fazla bağımsız örneğimiz varsa, örnek ortalaması ortalamanın doğru bir tahmini olacak ve nihai varyansı verecektir.

Parçacık filtresi optimalin altında olsa bile, parçacık sayısı sonsuza yaklaştıkça algoritmanın verimliliği Bayes tahmin kuralına yaklaşır. Bu nedenle mümkün olduğu kadar çok parçacığın elde edilmesi arzu edilir. en iyi sonuç. Ne yazık ki bu, hesaplamaların karmaşıklığında güçlü bir artışa yol açar ve sonuç olarak doğruluk ile hesaplama hızı arasında bir uzlaşmaya zorlar. Bu nedenle parçacık sayısı doğruluk değerlendirme görevinin gereksinimlerine göre seçilmelidir. Partikül filtresinin çalışması için bir diğer önemli faktör örnekleme hızının sınırlandırılmasıdır. Daha önce de belirtildiği gibi, örnekleme hızı parçacık filtreleme için önemli bir parametredir ve bu olmadan algoritma eninde sonunda dejenere olacaktır. Buradaki fikir, eğer ağırlıklar çok dengesiz bir şekilde dağılmışsa ve örnekleme eşiğine ulaşılmak üzereyse, o zaman düşük ağırlıklı parçacıklar atılır ve geri kalan küme, yeni örneklerin alınabileceği yeni bir olasılık yoğunluğu oluşturur. Örnekleme hızı eşiğinin seçilmesi oldukça zor bir iştir, çünkü aynı zamanda yüksek frekans filtrenin gürültüye karşı aşırı duyarlı olmasına neden olur ve çok düşük olması büyük bir hataya neden olur. Ayrıca önemli bir faktör olasılık yoğunluğudur.

Genel olarak, parçacık filtreleme algoritması şunları gösterir: iyi performans Sabit hedefler için ve bilinmeyen hızlanma dinamiklerine sahip nispeten yavaş hareket eden hedefler durumunda konum hesaplaması. Genel olarak parçacık filtreleme algoritması, genişletilmiş Kalman filtresinden daha kararlıdır ve dejenerasyona ve ciddi arızalara daha az eğilimlidir. Doğrusal olmayan, Gaussian olmayan dağılım durumlarında bu algoritma filtreleme, hedefin konumunu belirlemede çok iyi bir doğruluk gösterirken, genişletilmiş Kalman filtreleme algoritması bu koşullar altında kullanılamaz. Bu yaklaşımın dezavantajları, genişletilmiş Kalman filtresine göre daha karmaşık olmasının yanı sıra, bu algoritma için doğru parametrelerin nasıl seçileceğinin her zaman açık olmamasıdır.

Bu alanda umut verici araştırmalar

Sunduğumuz modele benzer bir Kalman filtre modelinin kullanımı, entegre bir sistemin (coğrafi tabanla eşleştirme için GPS + bilgisayarlı görme modeli) performansını artırmak için kullanıldığı yerde görülebilir. Uydu navigasyon ekipmanının arızası da simüle edilmiştir. Kalman filtresi kullanılarak sistemin arıza durumunda sonuçları önemli ölçüde iyileştirildi (örneğin, yüksekliğin belirlenmesindeki hata yaklaşık iki kat, farklı eksenler boyunca koordinatların belirlenmesindeki hatalar neredeyse 9 kat azaldı) . Kalman filtresinin benzer bir kullanımı da verilmiştir.

Bir dizi yöntem açısından ilginç bir sorun . Ayrıca model yapısında bazı farklılıklar olmakla birlikte 5 durumlu Kalman filtresi kullanır. Elde edilen sonuç, ek entegrasyon araçlarının (fotoğraf ve termal görüntüleme görüntülerinin kullanılması) kullanılması nedeniyle sunduğumuz modelin sonucunu aşmaktadır. Bu durumda Kalman filtresinin kullanılması, belirli bir noktanın uzaysal koordinatlarının belirlenmesindeki hatayı 5,5 m değerine düşürmemize olanak tanır.

Çözüm

Sonuç olarak, Kalman filtresinin İHA konumlandırma sistemlerinde kullanımının birçok modern gelişmede uygulandığını not ediyoruz. Bu kullanımın, farklı durum faktörlerine sahip birkaç benzer filtrenin eşzamanlı kullanımına kadar çok sayıda varyasyonu ve yönü vardır. Kalman filtrelerinin geliştirilmesinde en umut verici yönlerden biri, hataları renkli gürültüyle temsil edilecek ve gerçek sorunların çözümünde onu daha da değerli hale getirecek değiştirilmiş bir filtrenin oluşturulması gibi görünüyor. Ayrıca alanda büyük ilgi gören, Gauss olmayan gürültüyü filtreleyebilen kısmi bir filtredir. Özellikle standart uydu navigasyon sistemlerinin arızalanması durumunda doğruluğun iyileştirilmesindeki bu çeşitlilik ve somut sonuçlar, bu teknolojinin çeşitli uçaklar için doğru ve hataya dayanıklı navigasyon sistemlerinin geliştirilmesiyle ilgili çeşitli bilimsel alanlar üzerindeki etkisindeki ana faktörlerdir. .

İnceleyenler:

Labunets V.G., Teknik Bilimler Doktoru, Profesör, Bölüm Profesörü teorik temeller Rusya'nın ilk Cumhurbaşkanı B.N.'nin adını taşıyan Ural Federal Üniversitesi radyo mühendisliği. Yeltsin, Yekaterinburg;

Ivanov V.E., Teknik Bilimler Doktoru, Profesör, Baş. Ural Federal Üniversitesi Teknoloji ve İletişim Bölümü, Rusya'nın ilk Cumhurbaşkanı B.N. Yeltsin, Yekaterinburg.

Bibliyografik bağlantı

Random Forest en sevdiğim veri madenciliği algoritmalarından biridir. İlk olarak, inanılmaz derecede çok yönlüdür; hem regresyon hem de sınıflandırma problemlerini çözmek için kullanılabilir. Anormallikleri arayın ve tahmin edicileri seçin. İkincisi, yanlış uygulanması gerçekten zor bir algoritmadır. Bunun nedeni, diğer algoritmalardan farklı olarak çok az özelleştirilebilir parametreye sahip olmasıdır. Ayrıca doğası gereği şaşırtıcı derecede basittir. Ve aynı zamanda inanılmaz derecede doğrudur.

Böyle harika bir algoritmanın ardındaki fikir nedir? Fikir basit: Diyelim ki çok zayıf bir algoritmamız var. Bu zayıf algoritmayı kullanarak birçok farklı model yaparsak ve tahminlerinin sonuçlarını ortalamaya alırsak, nihai sonuç çok daha iyi olacaktır. Buna eylem halinde topluluk öğrenimi denir. Rastgele Orman algoritması bu nedenle alınan veriler için “Rastgele Orman” olarak adlandırılır; birçok karar ağacı oluşturur ve ardından bunların tahminlerinin sonucunun ortalamasını alır. Burada önemli olan nokta, her ağacın yaratılışındaki tesadüf unsurudur. Sonuçta, çok sayıda özdeş ağaç oluşturursak, bunların ortalamasının sonucunun tek bir ağacın doğruluğuna sahip olacağı açıktır.

Nasıl çalışıyor? Bazı girdi verilerimizin olduğunu varsayalım. Her sütun bir parametreye, her satır ise bir veri öğesine karşılık gelir.

Tüm veri setinden belirli sayıda sütun ve satırı rastgele seçip bunlara dayalı bir karar ağacı oluşturabiliriz.

10 Mayıs 2012 Perşembe

12 Ocak 2012 Perşembe

Bunların hepsi Nisan 2011'de Zynga ile telefon görüşmesi yaptığımda başladı. Sonra her şey gerçeklikle ilgisi olmayan bir tür oyun gibi göründü ve bunun neye yol açacağını hayal bile edemedim. Haziran 2011'de Zynga Moskova'ya geldi ve bir dizi röportaj yaptı, telefon görüşmesini geçen yaklaşık 60 aday değerlendirildi ve bunlardan yaklaşık 15 kişi seçildi (tam sayıyı bilmiyorum, bazıları sonradan fikrini değiştirdi, diğerleri) hemen reddetti). Röportajın şaşırtıcı derecede basit olduğu ortaya çıktı. Programlama sorunu yok, taramaların şekliyle ilgili yanıltıcı sorular yok, çoğunlukla sohbet yeteneğinizi test ediyor. Ve bence bilgi yalnızca yüzeysel olarak değerlendirildi.

Ve sonra saçmalık başladı. Önce sonuçları bekledik, sonra teklifi, ardından LCA onayını, ardından vize dilekçesinin onayını, ardından ABD’den gelen belgeleri, ardından elçilik kuyruğunu, ardından ek doğrulamayı, ardından vizeyi bekledik. Bazen bana her şeyden vazgeçip gol atmaya hazırmışım gibi geldi. Bazen bu Amerika'ya ihtiyacımız olup olmadığından şüphe ettim, sonuçta Rusya da fena değil. Tüm süreç yaklaşık altı ay sürdü, sonunda Aralık ortasında vizeleri aldık ve yola çıkmaya hazırlanmaya başladık.

Pazartesi yeni bir yerdeki ilk iş günümdü. Ofis sadece çalışmak için değil aynı zamanda yaşamak için de tüm koşullara sahiptir. Kendi şeflerimizin hazırladığı kahvaltılar, öğle yemekleri ve akşam yemekleri, her köşeye doldurulmuş çok çeşitli yiyecekler, spor salonu, masaj ve hatta kuaför. Bütün bunlar çalışanlar için tamamen ücretsizdir. Birçok kişi işe bisikletle gidip geliyor ve bazı odalar araçları depolamak için donatılmış. Genel olarak Rusya'da hiç böyle bir şey görmedim. Ancak her şeyin bir bedeli var; çok çalışmamız gerektiği konusunda hemen uyarıldık. Onların standartlarına göre "çok"un ne olduğu benim için çok açık değil.

Ancak umuyorum ki, bu kadar iş yoğunluğuna rağmen, öngörülebilir gelecekte blog yazmaya devam edebilirim ve belki de Amerikan yaşamı ve Amerika'da programcı olarak çalışmam hakkında bir şeyler anlatabilirim. Bekle ve gör. Bu arada herkese Mutlu Yıllar ve Noel diliyorum ve tekrar görüşürüz!

Sonuç<- NULL for(i in (1:length(divs[,1]))){ d <- divs if (d$Divs>0)( deneyin(( tırnak işaretleri<- getSymbols(d$Symbol, src="Finam", from="2010-01-01", auto.assign=FALSE) if (!is.nan(quotes)){ price <- Cl(quotes) if (length(price)>0)(gg<- d$Divs result <- rbind(result, data.frame(d$Symbol, d$Name, d$RegistryDate, as.numeric(dd)/as.numeric(price), stringsAsFactors=FALSE)) } } }, silent=TRUE) } } colnames(result) <- c("Symbol", "Name", "RegistryDate", "Divs") result

Habré dahil olmak üzere internette Kalman filtresi hakkında birçok bilgi bulabilirsiniz. Ancak formüllerin kendisi hakkında kolayca sindirilebilir bir sonuç bulmak zordur. Sonuçsuz, tüm bu bilim bir tür şamanizm olarak algılanıyor, formüller meçhul bir semboller dizisi gibi görünüyor ve en önemlisi teorinin yüzeyinde yatan birçok basit ifade anlaşılamayacak durumda. Bu makalenin amacı bu filtreden mümkün olduğunca erişilebilir bir dilde bahsetmek olacaktır.
Kalman filtresi güçlü bir veri filtreleme aracıdır. Ana prensibi, filtrelemenin olayın fiziği hakkındaki bilgileri kullanmasıdır. Diyelim ki, bir arabanın hız göstergesindeki verileri filtrelerseniz, o zaman arabanın ataleti size hızdaki çok hızlı sıçramaları bir ölçüm hatası olarak algılama hakkı verir. Kalman filtresi ilginçtir çünkü bir bakıma en iyi filtredir. Aşağıda “en iyi” kelimesinin tam olarak ne anlama geldiğini daha detaylı olarak tartışacağız. Makalenin sonunda çoğu durumda formüllerin neredeyse hiçbir şey kalmayacak kadar basitleştirilebileceğini göstereceğim.

Eğitici program

Kalman filtresiyle tanışmadan önce olasılık teorisinden bazı basit tanımları ve gerçekleri hatırlamanızı öneririm.

Rastgele değer

Rastgele bir değişken verildiğini söylediklerinde bu değerin rastgele değerler alabileceğini kastediyorlar. Farklı olasılıklarla farklı değerler alır. Örneğin bir zar attığınızda, ayrı bir değerler kümesi görünecektir: . Örneğin başıboş bir parçacığın hızından bahsettiğimizde, açıkçası sürekli bir değerler dizisiyle uğraşmamız gerekir. Bir rastgele değişkenin "dışlanan" değerlerini ile göstereceğiz, ancak bazen rastgele değişkeni belirttiğimiz harfin aynısını kullanırız: .
Sürekli bir değerler kümesi durumunda, rastgele bir değişken, bir rastgele değişkenin belirli bir uzunluktaki küçük bir mahallede "düşme" olasılığının eşit olduğunu bize dikte eden bir olasılık yoğunluğu ile karakterize edilir. Resimden de görebileceğimiz gibi bu olasılık grafiğin altındaki taralı dikdörtgenin alanına eşittir:

Hayatta oldukça sık olarak, olasılık yoğunluğu eşit olduğunda rastgele değişkenler Gauss dağılımına sahiptir.

Fonksiyonun, merkezi bir noktada ve karakteristik genişlikte bir çan şekline sahip olduğunu görüyoruz.
Gauss dağılımından bahsettiğimiz için bunun nereden geldiğinden bahsetmemek ayıp olur. Sayıların matematikte sağlam bir şekilde yerleşmiş olması ve en beklenmedik yerlerde bulunması gibi, Gauss dağılımı da olasılık teorisinde derin kökler edinmiştir. Gauss'un her yerde bulunuşunu kısmen açıklayan dikkate değer bir ifade şudur:
Keyfi bir dağılıma sahip bir rastgele değişken olsun (aslında bu keyfiliğin bazı kısıtlamaları vardır, ancak bunlar hiç de katı değildir). Deneyler yapalım ve bir rastgele değişkenin "dışlanan" değerlerinin toplamını hesaplayalım. Bunun gibi birçok deney yapalım. Her seferinde miktarın farklı bir değerini alacağımız açıktır. Başka bir deyişle, bu miktarın kendisi de kendine özgü dağılım yasasına sahip bir rastgele değişkendir. Yeterince büyük olduğunda, bu toplamın dağılım yasasının Gauss dağılımına yöneldiği ortaya çıktı (bu arada, “zilin” karakteristik genişliği şu şekilde büyür). Wikipedia'da daha ayrıntılı olarak okuyoruz: merkezi limit teoremi. Hayatta çoğu zaman çok sayıda aynı şekilde dağıtılmış bağımsız rastgele değişkenlerin toplamı olan nicelikler vardır ve bu nedenle bunlar Gaussian olarak dağıtılır.

Ortalama değer

Bir rastgele değişkenin ortalama değeri, çok sayıda deney yürütürsek ve bırakılan değerlerin aritmetik ortalamasını hesaplarsak limitte elde edeceğimiz değerdir. Ortalama değer farklı şekillerde gösterilir: matematikçiler bunu (matematiksel beklenti) aracılığıyla ve yabancı matematikçiler (beklenti) aracılığıyla belirtmeyi severler. Fizikçiler veya aracılığıyla. Bunu yabancı bir şekilde belirleyeceğiz: .
Örneğin, Gauss dağılımı için ortalama şudur.

Dağılım

Gauss dağılımı durumunda, rastgele değişkenin ortalama değerinin belirli bir mahallesine düşmeyi tercih ettiğini açıkça görüyoruz. Grafikten görülebileceği gibi değerlerin karakteristik yayılımı mertebesindedir. Dağılımını biliyorsak, keyfi bir rastgele değişken için bu değer dağılımını nasıl tahmin edebiliriz? Olasılık yoğunluğunun bir grafiğini çizebilir ve karakteristik genişliğini gözle tahmin edebilirsiniz. Ama biz cebirsel yola gitmeyi tercih ediyoruz. Ortalama sapma uzunluğunu (modülü) ortalama değerden bulabilirsiniz: . Bu değer, değerlerin karakteristik yayılımının iyi bir tahmini olacaktır. Ancak siz ve ben, formüllerdeki modülleri kullanmanın baş ağrısı olduğunu çok iyi biliyoruz, bu nedenle bu formül, karakteristik saçılımı tahmin etmek için nadiren kullanılır.
Daha basit bir yol (hesaplamalar açısından basit) bulmaktır. Bu miktara dispersiyon denir ve sıklıkla şu şekilde gösterilir: Varyansın köküne standart sapma denir. Standart sapma, rastgele bir değişkenin yayılmasının iyi bir tahminidir.
Örneğin Gauss dağılımı için yukarıda tanımlanan varyansın tam olarak eşit olduğunu hesaplayabiliriz, bu da standart sapmanın eşit olduğu anlamına gelir ve bu da geometrik sezgimizle çok iyi uyum sağlar.
Aslında burada küçük bir dolandırıcılık gizlidir. Gerçek şu ki Gauss dağılımının tanımında üssün altında bir ifade var. Bu ikisi tam olarak paydada olduğundan standart sapma katsayıya eşit olacaktır. Yani, Gauss dağılım formülünün kendisi, standart sapmasını hesaplayabilmemiz için özel olarak uyarlanmış bir biçimde yazılmıştır.

Bağımsız rastgele değişkenler

Rastgele değişkenler bağımlı olabilir veya olmayabilir. Bir uçağa bir iğne attığınızı ve her iki ucun koordinatlarını kaydettiğinizi hayal edin. Bu iki koordinat bağımlıdır; rastgele değişkenler olmalarına rağmen aralarındaki mesafenin her zaman iğnenin uzunluğuna eşit olması koşuluyla ilişkilidirler.
Rastgele değişkenler, birincisinin sonucu ikincinin sonucundan tamamen bağımsızsa bağımsızdır. Rastgele değişkenler bağımsızsa, çarpımlarının ortalama değeri ortalama değerlerinin çarpımına eşittir:

Kanıt

Örneğin mavi gözlü olmak ve okuldan altın madalyayla mezun olmak bağımsız rastgele değişkenlerdir. Diyelim ki mavi gözlüler altın madalyalıysa, o zaman mavi gözlü madalyalılar. Bu örnek bize, rastgele değişkenlerin olasılık yoğunluklarına göre belirtilmesi durumunda bu değerlerin bağımsızlığının olasılık yoğunluğunun () ile ifade edildiğini anlatır. ilk değer çıkarılmıştır ve ikincisi) aşağıdaki formülle bulunur:

Bundan hemen şu sonuç çıkıyor:

Gördüğünüz gibi ispat, sürekli bir değer spektrumuna sahip olan ve olasılık yoğunluklarına göre belirlenen rastgele değişkenler için gerçekleştirildi. Diğer durumlarda ispat fikri benzerdir.

Kalman filtresi

Sorunun formülasyonu

Ölçüp filtreleyeceğimiz değeri belirtelim. Bu konum, hız, hızlanma, nem, koku derecesi, sıcaklık, basınç vb. olabilir.
Bizi genel problemin formülasyonuna götürecek basit bir örnekle başlayalım. Yalnızca ileri ve geri gidebilen, radyo kontrollü bir arabamız olduğunu hayal edin. Arabanın ağırlığını, şeklini, yol yüzeyini vb. bilerek kontrol joystick'inin hareket hızını nasıl etkilediğini hesapladık.

Daha sonra arabanın koordinatları kanuna göre değişecektir:

Gerçek hayatta, araca etkiyen küçük rahatsızlıkları (rüzgar, tümsekler, yoldaki çakıl taşları) hesaplamalarımızda hesaba katamayız, bu nedenle arabanın gerçek hızı hesaplanandan farklı olacaktır. Yazılı denklemin sağ tarafına bir rastgele değişken eklenecektir:

Arabanın gerçek koordinatını ölçmeye çalışan ve elbette bunu doğru bir şekilde ölçemeyen, ancak yine de rastgele bir değişken olan bir hatayla ölçen, arabaya takılı bir GPS sensörümüz var. Sonuç olarak sensörden hatalı veriler alıyoruz:

Görev, yanlış sensör okumalarını bilerek arabanın gerçek koordinatı için iyi bir yaklaşım bulmaktır.
Genel problemin formülasyonunda koordinattan herhangi bir şey sorumlu olabilir (sıcaklık, nem…) ve sistemi dışarıdan kontrol etmekten sorumlu üyeyi (makine örneğinde) olarak belirteceğiz. Koordinatlar ve sensör okumaları için denklemler şöyle görünecektir:

Bildiklerimizi ayrıntılı olarak tartışalım:

Filtreleme görevinin bir yumuşatma görevi olmadığını belirtmekte fayda var. Sensör verilerini yumuşatmaya çalışmıyoruz, gerçek koordinata en yakın değeri elde etmeye çalışıyoruz.

Kalman algoritması

Tümevarım yoluyla tartışacağız. Üçüncü adımda sensörden sistemin gerçek koordinatına oldukça yakın olan filtrelenmiş bir değer bulduğumuzu hayal edin. Bilinmeyen koordinattaki değişimi kontrol eden denklemi bildiğimizi unutmayın:

dolayısıyla henüz sensörden değer almadan, bu adımda sistemin bu yasaya göre gelişeceğini ve sensörün 'ye yakın bir şey göstereceğini varsayabiliriz. Ne yazık ki henüz daha kesin bir şey söyleyemeyiz. Öte yandan, adım sırasında elimizde hatalı bir sensör okuması olacaktır.
Kalman'ın fikri şu şekildedir. Gerçek koordinata en iyi yaklaşımı elde etmek için, hatalı sensörün okuması ile onun görmesini beklediğimiz tahmin arasında bir orta yol seçmeliyiz. Sensör okumasına bir ağırlık vereceğiz ve tahmin edilen değerde bir ağırlık kalacaktır:

Katsayıya Kalman katsayısı denir. Yineleme adımına bağlıdır, bu nedenle yazmak daha doğru olur, ancak şimdilik hesaplama formüllerini karıştırmamak için dizinini atlayacağız.
Kalman katsayısını, elde edilen optimal koordinat değerinin gerçeğe en yakın olacağı şekilde seçmeliyiz. Örneğin sensörümüzün çok doğru olduğunu biliyorsak, onun okumasına daha çok güveniriz ve değere daha fazla ağırlık veririz (bire yakın). Aksine, sensör hiç doğru değilse, o zaman teorik olarak tahmin edilen değere daha çok odaklanacağız.
Genel olarak Kalman katsayısının tam değerini bulmak için hatayı en aza indirmeniz yeterlidir:

Hatanın ifadesini yeniden yazmak için denklemleri (1) (çerçevedeki mavi arka planda olanlar) kullanırız:

Kanıt

Şimdi hatayı en aza indirme ifadesinin ne anlama geldiğini tartışmanın zamanı geldi mi? Sonuçta hatanın kendisi de rastgele bir değişkendir ve her seferinde farklı değerler alır. Minimum hataya sahip olmanın ne anlama geldiğini tanımlamaya yönelik aslında herkese uyan tek bir yaklaşım yoktur. Rastgele bir değişkenin dağılımında olduğu gibi, dağılımının karakteristik genişliğini tahmin etmeye çalıştığımızda, burada hesaplamalar için en basit kriteri seçeceğiz. Karesel hatanın ortalamasını en aza indireceğiz:

Son ifadeyi yazalım:

Kanıt

For ifadesinde yer alan tüm rastgele değişkenlerin bağımsız olduğu gerçeğinden, tüm "çapraz" terimlerin sıfıra eşit olduğu sonucu çıkar:

Varyans formülünün çok daha basit göründüğü gerçeğini kullandık: .

Bu ifade şu durumlarda minimum değer alır (türevi sıfıra eşitlersek):

Burada zaten Kalman katsayısı için adım indeksi ile bir ifade yazıyoruz, dolayısıyla bunun yineleme adımına bağlı olduğunu vurguluyoruz.
Ortaya çıkan optimal değeri, küçülttüğümüz ifadenin yerine koyarız. Anlıyoruz;

Sorunumuz çözüldü. Kalman katsayısını hesaplamak için yinelemeli bir formül elde ettik.
Edindiğimiz bilgileri tek bir çerçevede özetleyelim:

Örnek

Matlab kodu

Hepsini temizle; N=%100 örnek sayısı a=%0,1 ivme sigmaPsi=1 sigmaEta=50; k=1:N x=k x(1)=0 z(1)=x(1)+normrnd(0,sigmaEta); t=1 için:(N-1) x(t+1)=x(t)+a*t+normrnd(0,sigmaPsi); z(t+1)=x(t+1)+normrnd(0,sigmaEta); son; %kalman filtresi xOpt(1)=z(1); eOpt(1)=sigmaEta; t=1 için:(N-1) eOpt(t+1)=sqrt((sigmaEta^2)*(eOpt(t)^2+sigmaPsi^2)/(sigmaEta^2+eOpt(t)^2+ sigmaPsi^2)) K(t+1)=(eOpt(t+1))^2/sigmaEta^2 xOpt(t+1)=(xOpt(t)+a*t)*(1-K(t) +1))+K(t+1)*z(t+1) uç; arsa(k,xOpt,k,z,k,x)

Analiz

Kalman katsayısının yineleme adımlarıyla nasıl değiştiğini izlerseniz, onun her zaman belirli bir değerde sabitlendiğini gösterebilirsiniz. Örneğin, sensör ve modelin kök ortalama kare hataları on/bir oranına sahip olduğunda, iterasyon adımına bağlı olarak Kalman katsayısının grafiği şu şekilde görünür:

Aşağıdaki örnekte bunun hayatımızı nasıl kolaylaştırabileceğini tartışacağız.

İkinci örnek

Uygulamada sıklıkla filtrelediğimiz şeyin fiziksel modeli hakkında hiçbir şey bilmediğimiz görülür. Örneğin, en sevdiğiniz ivmeölçerden gelen değerleri filtrelemek istediniz. İvme ölçeri hangi yasaya göre döndürmeyi planladığınızı önceden bilmiyorsunuz. Toplayabileceğiniz en fazla bilgi sensör hatası varyansıdır. Böyle zor bir durumda, hareket modeline ilişkin tüm bilgisizlik, rastgele bir değişkene yönlendirilebilir:

Ancak açıkçası böyle bir sistem artık rastgele değişkene dayattığımız koşulları karşılamıyor çünkü artık tüm bilinmeyen hareket fiziği orada gizli ve bu nedenle farklı zaman anlarındaki model hatalarının bağımsız olduğunu söyleyemeyiz. birbirlerinin olduğunu ve ortalama değerlerinin sıfır olduğunu. Bu durumda Kalman filtre teorisi genel olarak uygulanamaz. Ancak, bu gerçeğe dikkat etmeyeceğiz, ancak filtrelenen verilerin güzel görünmesi için katsayıları gözle seçerek tüm devasa formülleri aptalca uygulayacağız.
Ancak farklı, çok daha basit bir yol seçebilirsiniz. Yukarıda da gördüğümüz gibi Kalman katsayısı arttıkça her zaman aynı değerde sabitlenir. Dolayısıyla katsayıları seçmek ve karmaşık formüller kullanarak Kalman katsayısını bulmak yerine, bu katsayıyı her zaman bir sabit olarak kabul edip sadece bu sabiti seçebiliriz. Bu varsayım neredeyse hiçbir şeyi bozmaz. Birincisi, Kalman teorisini zaten yasa dışı olarak kullanıyoruz ve ikincisi, Kalman katsayısı hızla sabit bir noktaya geliyor. Sonunda her şey çok daha basit olacak. Kalman'ın teorisindeki herhangi bir formüle ihtiyacımız yok, sadece kabul edilebilir bir değer seçip onu yinelemeli formüle eklememiz gerekiyor:

Aşağıdaki grafik, hayali bir sensörden iki farklı şekilde filtrelenen verileri göstermektedir. Tabii olayın fiziği hakkında hiçbir şey bilmememiz şartıyla. İlk yöntem, Kalman'ın teorisindeki tüm formülleri içeren dürüst bir yöntemdir. İkincisi ise formüller olmadan basitleştirilmiştir.

Gördüğümüz gibi yöntemler neredeyse hiç farklı değil. Kalman katsayısının henüz stabil olmadığı başlangıçta küçük bir fark gözlenir.

Tartışma

Gördüğümüz gibi Kalman filtresinin ana fikri, filtrelenen değeri sağlayacak bir katsayı bulmaktır.

ortalama olarak koordinatın gerçek değerinden en az farklı olacaktır. Filtrelenen değerin, sensör okumasının ve önceki filtrelenen değerin doğrusal bir fonksiyonu olduğunu görüyoruz. Ve önceki filtrelenen değer, sensör okumasının ve önceki filtrelenen değerin doğrusal bir fonksiyonudur. Ve zincir tamamen dönene kadar böyle devam eder. Yani, filtrelenen değer şunlara bağlıdır: herkesÖnceki sensör okumaları doğrusal olarak:

Bu nedenle Kalman filtresine doğrusal filtre adı verilir.
Tüm doğrusal filtreler arasında Kalman filtresinin en iyisi olduğu kanıtlanabilir. Ortalama kare filtre hatasının minimum düzeyde olması açısından en iyisi.

Çok boyutlu kasa

Kalman filtresinin tüm teorisi çok boyutlu duruma genelleştirilebilir. Buradaki formüller biraz daha korkutucu görünüyor ancak bunları türetme fikri tek boyutlu durumdakiyle aynı. Bunları şu harika makalede görebilirsiniz: http://habrahabr.ru/post/140274/.
Ve bu harikada video Bunların nasıl kullanılacağına dair bir örnek verilmiştir.