Информационен портал за сигурност. Филтриране на Калман Филтър на Калман за скаларни измервания

Wiener филтрите са най-подходящи за обработка на процеси или сегменти от процеси като цяло (блокова обработка). Последователната обработка изисква текуща оценка на сигнала при всеки цикъл, като се вземе предвид информацията, получена на входа на филтъра по време на процеса на наблюдение.

С Wiener филтриране всяка нова проба от сигнала ще изисква преизчисляване на всички тегла на филтъра. Понастоящем широко се използват адаптивни филтри, при които входящите нова информацияизползва се за непрекъсната корекция на предварително направена оценка на сигнала (проследяване на целта в РЛС, автоматични системи за управление при управление и др.). От особен интерес са адаптивните филтри от рекурсивен тип, известни като филтър на Калман.

Тези филтри се използват широко в управляващите контури в системите за автоматично регулиране и управление. Това е мястото, откъдето идват, както се вижда от такава специфична терминология, използвана при описанието на тяхната работа като пространство на държавата.

Една от основните задачи, които трябва да бъдат решени в практиката на невронните изчисления, е получаването на бързи и надеждни алгоритми за обучение на невронни мрежи. В това отношение може да е полезно да се използва алгоритъм за обучение на линейни филтри в обратната връзка. Тъй като алгоритмите за обучение са итеративни по природа, такъв филтър трябва да бъде последователен рекурсивен оценител.

Проблем с оценката на параметрите

Един от проблемите на теорията на статистическите решения, който е от голямо практическо значение, е проблемът за оценка на векторите на състоянието и параметрите на системите, който се формулира по следния начин. Да предположим, че е необходимо да се оцени стойността на векторния параметър $X$, който е недостъпен за директно измерване. Вместо това се измерва друг параметър $Z$, в зависимост от $X$. Задачата на оценката е да се отговори на въпроса: какво може да се каже за $X$ при $Z$. В общия случай процедурата за оптимална оценка на вектора $X$ зависи от приетия критерий за качество на оценката.

Например, байесовият подход към проблема с оценката на параметъра изисква пълна априорна информация за вероятностните свойства на оценявания параметър, което често е невъзможно. В тези случаи се прибягва до метода на най-малките квадрати (LSM), който изисква много по-малко априорна информация.

Нека разгледаме приложението на най-малките квадрати за случая, когато векторът на наблюдение $Z$ е свързан с вектора за оценка на параметъра $X$ чрез линеен модел и в наблюдението има шум $V$, който не е корелиран с прогнозен параметър:

$Z = HX + V$, (1)

където $H$ е трансформационната матрица, описваща връзката между наблюдаваните стойности и оценените параметри.

Оценката $X$, минимизираща грешката на квадрат, се записва, както следва:

$X_(ots)=(H^TR_V^(-1)H)^(-1)H^TR_V^(-1)Z$, (2)

Нека шумът $V$ не е корелиран, в който случай матрицата $R_V$ е само матрицата на идентичност и уравнението за оценка става по-просто:

$X_(ots)=(H^TH)^(-1)H^TZ$, (3)

Записването в матрична форма значително спестява хартия, но може да е необичайно за някого. Следният пример, взет от монографията на Ю. М. Коршунов "Математически основи на кибернетиката", илюстрира всичко това.
Има следната електрическа верига:

Наблюдаваните стойности в този случай са показанията на инструмента $A_1 ​​​​= 1 A, A_2 = 2 A, V = 20 B$.

Освен това е известно съпротивлението $R = 5$ Ohm. Необходимо е да се оценят по най-добрия начин, от гледна точка на критерия за минимална средна квадратична грешка, стойностите на токовете $I_1$ и $I_2$. Най-важното тук е, че има някаква връзка между наблюдаваните стойности (отчитания на инструмента) и оценените параметри. И тази информация се внася отвън.

В този случай това са законите на Кирхоф, в случая на филтриране (за което ще стане дума по-късно) - авторегресивен модел на времеви редове, който предполага, че текущата стойност зависи от предишните.

Така че познаването на законите на Кирхоф, което по никакъв начин не е свързано с теорията на статистическите решения, ви позволява да установите връзка между наблюдаваните стойности и оценените параметри (тези, които са учили електротехника, могат да проверят, останалите ще трябва да повярвайте на думата им):

$$z_1 = A_1 = I_1 + \xi_1 = 1$$

$$z_2 = A_2 = I_1 + I_2 + \xi_2 = 2$$

$$z_2 = V/R = I_1 + 2 * I_2 + \xi_3 = 4$$

Това е във векторна форма:

$$\begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) \begin(vmatrix) I_1\ \ I_2 \end(vmatrix) + \begin(vmatrix) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrix)$$

Или $Z = HX + V$, където

$$Z= \begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1\\ 2\\ 4 \end(vmatrix) ; H= \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) ; X= \begin(vmatrix) I_1\\ I_2 \end(vmatrix) ; V= \begin(vmatrix) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrix)$$

Като се имат предвид стойностите на шума като некорелирани помежду си, намираме оценката на I 1 и I 2 по метода на най-малките квадрати в съответствие с формула 3:

$H^TH= \begin(vmatrix) 1 & 1& 1\\ 0 & 1& 2 \end(vmatrix) \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) = \ начало (vmatrix) 3 & 3\\ 3 & 5 \end(vmatrix) ; (H^TH)^(-1)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) $;

$H^TZ= \begin(vmatrix) 1 & 1& 1\\ 0 & 1& 2 \end(vmatrix) \begin(vmatrix) 1 \\ 2\\ 4 \end(vmatrix) = \begin(vmatrix) 7\ \ 10 \end(vmatrix) ; X(vmatrix)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) \begin(vmatrix) 7\\ 10 \end(vmatrix) = \frac (1)(6) \begin(vmatrix) 5\\ 9 \end(vmatrix)$;

Така че $I_1 = 5/6 = 0,833 A$; $I_2 = 9/6 = 1,5 A$.

Задача за филтриране

За разлика от проблема за оценка на параметри, които имат фиксирани стойности, при проблема с филтрирането се изисква да се оценят процесите, тоест да се намерят текущи оценки на променящ се във времето сигнал, изкривен от шум и следователно недостъпен за директно измерване. В общия случай видът на филтриращите алгоритми зависи от статистическите свойства на сигнала и шума.

Ще приемем, че полезният сигнал е бавно променяща се функция на времето, а шумът е некорелиран шум. Ще използваме метода на най-малките квадрати, отново поради липсата на априорна информация за вероятностните характеристики на сигнала и шума.

Първо, получаваме оценка на текущата стойност на $x_n$, като използваме последните $k$ стойности на времевия ред $z_n, z_(n-1),z_(n-2)\dots z_(n-( k-1))$. Моделът на наблюдение е същият като в задачата за оценка на параметъра:

Ясно е, че $Z$ е колонен вектор, състоящ се от наблюдаваните стойности на времевия ред $z_n, z_(n-1),z_(n-2)\dots z_(n-(k-1)) $, $V $ – вектор на шумовата колона $\xi _n, \xi _(n-1),\xi_(n-2)\dots \xi_(n-(k-1))$, изкривяващ истинския сигнал. И какво означават символите $H$ и $X$? За какъв вид колонен вектор $X$, например, можем да говорим, ако всичко, което е необходимо, е да се даде оценка на текущата стойност на времевия ред? А какво се има предвид под трансформационната матрица $H$ изобщо не е ясно.

На всички тези въпроси може да се отговори само ако се вземе под внимание концепцията за модел на генериране на сигнал. Тоест, необходим е някакъв модел на оригиналния сигнал. Това е разбираемо, при липса на априорна информация за вероятностните характеристики на сигнала и шума, остава само да се правят предположения. Можете да го наречете гадаене на утайката от кафе, но експертите предпочитат друга терминология. В техния сешоар това се нарича параметричен модел.

В този случай се оценяват параметрите на този конкретен модел. Когато избирате подходящ модел за генериране на сигнал, не забравяйте, че всяка аналитична функция може да бъде разширена в серия на Тейлър. Удивителното свойство на реда на Тейлър е, че формата на функция на всяко крайно разстояние $t$ от някаква точка $x=a$ се определя еднозначно от поведението на функцията в безкрайно малка околност на точката $x=a $ (говорим за неговите производни от първи и по-висок ред).

По този начин съществуването на редица на Тейлър означава, че аналитичната функция има вътрешна структура с много силна връзка. Ако, например, се ограничим до три члена от серията Тейлър, тогава моделът за генериране на сигнал ще изглежда така:

$x_(n-i) = F_(-i)x_n$, (4)

$$X_n= \begin(vmatrix) x_n\\ x"_n\\ x""_n \end(vmatrix) ; F_(-i)= \begin(vmatrix) 1 & -i & i^2/2\\ 0 & 1 & -i\\ 0 & 0 & 1 \end(vmatrix) $$

Тоест формула 4 с даден ред на полинома (в примера е равен на 2) установява връзка между $n$-та стойност на сигнала във времевата последователност и $(n-i)$-та . По този начин оцененият вектор на състоянието в този случай включва, в допълнение към самата оценена стойност, първата и втората производни на сигнала.

В теорията на автоматичното управление такъв филтър би се нарекъл астатичен филтър от втори ред. Трансформационната матрица $H$ за този случай (оценката се основава на текущата и $k-1$ предишни проби) изглежда така:

$$H= \begin(vmatrix) 1 & -k & k^2/2\\ - & - & -\\ 1 & -2 & 2\\ 1 & -1 & 0,5\\ 1 & 0 & 0 \ край (vmatrix)$$

Всички тези числа са получени от серията на Тейлър, като се приема, че интервалът от време между съседни наблюдавани стойности е постоянен и равен на 1.

По този начин проблемът с филтрирането, при нашите предположения, е сведен до проблема с оценката на параметрите; в този случай се оценяват параметрите на възприетия от нас модел за генериране на сигнал. И оценката на стойностите на вектора на състоянието $ X $ се извършва по същата формула 3:

$$X_(ots)=(H^TH)^(-1)H^TZ$$

Всъщност ние внедрихме процес на параметрична оценка, базиран на авторегресивен модел на процеса на генериране на сигнал.

Формула 3 лесно се внедрява в софтуер, за това трябва да попълните матрицата $H$ и векторната колона на наблюденията $Z$. Такива филтри се наричат филтри с ограничена памет, тъй като те използват последните $k$ наблюдения, за да получат текущата оценка $X_(not)$. При всяка нова стъпка на наблюдение, нов набор от наблюдения се добавя към текущия набор от наблюдения и старият се изхвърля. Този процес на оценка се нарича плъзгащ се прозорец.

Нарастващи филтри за памет

Филтрите с ограничена памет имат основния недостатък, че след всяко ново наблюдение е необходимо да се извършва повторно пълно преизчисляване на всички данни, съхранени в паметта. В допълнение, изчисляването на оценките може да започне едва след натрупването на резултатите от първите $k$ наблюдения. Тоест тези филтри имат голяма продължителност на преходния процес.

За да се справите с този недостатък, е необходимо да преминете от филтър с постоянна памет към филтър с нарастваща памет. В такъв филтър броят на наблюдаваните стойности, които трябва да бъдат оценени, трябва да съответства на числото n на текущото наблюдение. Това дава възможност да се получат оценки, като се започне от броя на наблюденията, равен на броя на компонентите на оценения вектор $X$. И това се определя от реда на възприетия модел, тоест колко членове от серията на Тейлър се използват в модела.

В същото време, с увеличаване на n, изглаждащите свойства на филтъра се подобряват, т.е. точността на оценките се увеличава. Директното прилагане на този подход обаче е свързано с увеличаване на изчислителните разходи. Следователно филтрите за нарастваща памет се изпълняват като рецидивиращ.

Въпросът е, че към момента n вече имаме оценката $X_((n-1)ots)$, която съдържа информация за всички предишни наблюдения $z_n, z_(n-1), z_(n-2) \dots z_ (n-(k-1))$. Оценката $X_(not)$ се получава от следващото наблюдение $z_n$, като се използва информацията, съхранена в оценката $X_((n-1))(\mbox (ot))$. Тази процедура се нарича повтарящо се филтриране и се състои от следното:

• според оценката $X_((n-1))(\mbox (ots))$, оценката $X_n$ се ​​прогнозира от формула 4 за $i = 1$: $X_(\mbox (noca priori)) = F_1X_((n-1 )ots)$. Това е априорна оценка;
• според резултатите от текущото наблюдение $z_n$ тази априорна оценка се превръща в истинска, т.е. апостериорна;
• тази процедура се повтаря на всяка стъпка, започвайки от $r+1$, където $r$ е редът на филтъра.

Крайната формула за рекурсивно филтриране изглежда така:

$X_((n-1)ots) = X_(\mbox (нокаприори)) + (H^T_nH_n)^(-1)h^T_0(z_n - h_0 X_(\mbox (нокаприори)))$, (6 )

където за нашия филтър от втори ред:

Филтърът за нарастваща памет, който работи по формула 6, е специален случай на алгоритъма за филтриране, известен като филтър на Калман.

При практическото прилагане на тази формула трябва да се помни, че включената в нея априорна оценка се определя от формула 4, а стойността $h_0 X_(\mbox (nocapriori))$ е първият компонент на вектора $X_( \mbox (нокаприори))$.

Филтърът за нарастваща памет има една важна характеристика. Разглеждайки Формула 6, крайният резултат е сумата от прогнозния вектор на резултата и корекционния член. Тази корекция е голяма за малки $n$ и намалява с нарастването на $n$, като клони към нула при $n \rightarrow \infty$. Тоест, с нарастването на n, изглаждащите свойства на филтъра растат и моделът, вграден в него, започва да доминира. Но реалният сигнал може да съответства на модела само на отделни секции, така че точността на прогнозата се влошава.

За да се бори с това, започвайки от някои $n$, се налага забрана за по-нататъшно намаляване на срока за корекция. Това е еквивалентно на промяна на обхвата на филтъра, тоест за малки n филтърът е по-широколентов (по-малко инерционен), за големи n той става по-инерционен.

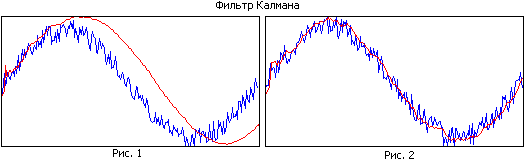
Сравнете Фигура 1 и Фигура 2. На първата фигура филтърът има голяма памет, докато изглажда добре, но поради тясната лента очакваната траектория изостава от реалната. Във втората фигура филтърната памет е по-малка, изглажда по-зле, но проследява реалната траектория по-добре.

Литература

1. Ю.М.Коршунов "Математически основи на кибернетиката"
2. А.В.Балакришнан "Теория на филтрацията на Калман"
3. В. Н. Фомин "Повтаряща се оценка и адаптивно филтриране"
4. C.F.N. Cowen, P.M. Предоставяне на „Адаптивни филтри“

Фиг. 1

Така двойката, която търсим, лежи някъде на тази права линия. Повтарям, невъзможно е да се избере от всички тези опции двойката, която действително съществуваше - която даде числото 12, без да има допълнителни улики. Въпреки това, в ситуацията, за която е изобретен филтърът на Калман, има такива намеци. Има нещо, което се знае предварително за случайните числа. По-специално там е известна така наречената хистограма на разпределение за всяка двойка числа. Обикновено се получава след достатъчно дълги наблюдения на падането на тези много случайни числа. Тоест, например, от опит е известно, че в 5% от случаите обикновено отпада двойката x=1, y=8 (означаваме тази двойка по следния начин: (1,8)), в 2% от случаите двойка x=2, y=3 ( 2.3), в 1% от случаите двойка (3.1), в 0.024% от случаите двойка (11.1) и т.н. Отново тази хистограма е зададена за всички двойкичисла, включително тези, които се събират до 12. Така за всяка двойка, която дава сбор до 12, можем да кажем, че например двойката (1, 11) отпада в 0,8% от случаите, двойката ( 2, 10) - в 1% от случаите, двойка (3, 9) - в 1,5% от случаите и т.н. По този начин можем да определим от хистограмата в какъв процент от случаите сумата от членовете на двойката е 12. Нека например в 30% от случаите сумата дава 12. А в останалите 70% останалите двойки падат out - това са (1.8), (2, 3), (3,1) и т.н. - тези, които се събират до числа, различни от 12. Нещо повече, нека например двойка (7,5) изпадне в 27% от случаите, докато всички останали двойки, които дават общо 12, изпаднат в 0,024% + 0,8% + 1%+1,5%+...=3% от случаите. И така, според хистограмата установихме, че числата, даващи общо 12, изпадат в 30% от случаите. В същото време знаем, че ако паднат 12, най-често (27% от 30%) причината за това е чифт (7,5). Тоест, ако вече 12 се хвърлят, можем да кажем, че в 90% (27% от 30% - или, което е същото, 27 пъти от всеки 30) причината за хвърлянето на 12 е чифт (7,5). Знаейки, че двойката (7.5) най-често е причината за получаване на сумата, равна на 12, логично е да се предположи, че най-вероятно тя е изпаднала сега. Разбира се, все още не е факт, че числото 12 всъщност се формира от тази конкретна двойка, но следващия път, ако срещнем 12 и отново приемем двойка (7,5), тогава някъде в 90% от случаите Ние сме 100% прав. Но ако приемем двойка (2, 10), ще бъдем прави само 1% от 30% от времето, което се равнява на 3,33% правилни предположения в сравнение с 90% при познаване на двойка (7,5). Това е всичко - това е смисълът на алгоритъма за филтър на Калман. Тоест филтърът на Калман не гарантира, че няма да направи грешка при определяне на сбора, но гарантира, че ще направи грешка минималния брой пъти (вероятността за грешка ще бъде минимална), тъй като използва статистика - хистограма на изпадане на двойки числа. Трябва също да се подчертае, че така наречената плътност на разпределение на вероятностите (PDD) често се използва в алгоритъма за филтриране на Калман. Трябва обаче да се разбере, че значението там е същото като това на хистограмата. Освен това хистограмата е функция, изградена на базата на PDF и е негова апроксимация (вижте например ).
По принцип можем да изобразим тази хистограма като функция на две променливи - тоест като вид повърхност над равнината xy. Когато повърхността е по-висока, вероятността съответната двойка да изпадне също е по-висока. Фигура 2 показва такава повърхност.

фиг.2

Както можете да видите, над линията x + y = 12 (които са варианти на двойки, даващи общо 12), има повърхностни точки на различни височини и най-високата височина е във варианта с координати (7,5). И когато попаднем на сбор равен на 12, в 90% от случаите двойката (7,5) е причина за появата на този сбор. Тези. именно тази двойка, която дава 12, има най-голяма вероятност да се появи, при условие че сумата е 12.
По този начин идеята зад филтъра на Калман е описана тук. Именно върху него се изграждат всякакви негови модификации - едностъпкови, многостъпкови рекурентни и т.н. За по-задълбочено изучаване на филтъра на Калман препоръчвам книгата: Van Tries G. Theory of detection, estimation and modulation.

p.s.За тези, които се интересуват от обяснение на концепциите на математиката, така нареченото „на пръсти“, можем да препоръчаме тази книга и по-специално главите от нейния раздел „Математика“ (можете да закупите самата книга или отделни глави от то).

Направено е изследване на използването на филтъра на Калман в съвременните разработки на комплекси навигационни системи. Даден е и анализиран пример за конструкция математически модел, който използва разширен филтър на Калман за подобряване на точността на определяне на координатите на безпилотни летателни апарати. Разгледан е частичният филтър. Направено кратък преглед научни трудовеизползване на този филтър за подобряване на надеждността и устойчивостта на грешки на навигационните системи. Тази статия ни позволява да заключим, че използването на филтъра на Калман в системите за позициониране на UAV се практикува в много съвременни разработки. Има огромен брой вариации и аспекти на тази употреба, които също дават осезаеми резултати за подобряване на точността, особено в случай на повреда на стандартните сателитни навигационни системи. Това е основният фактор за влиянието на тази технология върху различни научни области, свързани с разработването на точни и устойчиви на грешки навигационни системи за различни летателни апарати.

Калман филтър

навигация

безпилотен летателен апарат (БЛА)

1. Макаренко Г.К., Алешечкин А.М. Изследване на алгоритъма за филтриране при определяне на координатите на обект от сигналите на спътниковите радионавигационни системи Доклади ТУСУР. - 2012. - № 2 (26). - С. 15-18.

2. Bar-Shalom Y., Li X. R., Kirubarajan T. Оценка с приложения

за проследяване и навигация // Теоретични алгоритми и софтуер. - 2001. - кн. 3. - С. 10-20.

3. Басем И.С. Визуална навигация (VBN) на безпилотни летателни апарати (UAV) // УНИВЕРСИТЕТ В КАЛГАРИ. - 2012. - кн. 1. - С. 100-127.

4. Conte G., Doherty P. Интегрирана навигационна система за UAV, базирана на съпоставяне на въздушни изображения // Aerospace Conference. - 2008. -Кн. 1. - С. 3142-3151.

5. Guoqiang M., Drake S., Anderson B. Дизайн на разширен Калманов филтър за локализиране на UAV // Информация, решение и контрол. - 2007. - кн. 7. – С. 224–229.

6. Оптимизация на траекторията на Ponda S.S за локализиране на целта с помощта на малки безпилотни летателни апарати // Масачузетски технологичен институт. - 2008. - кн. 1. - С. 64-70.

7. Wang J., Garrat M., Lambert A. Интегриране на gps/ins/vision сензори за навигация на безпилотни летателни апарати // IAPRS&SIS. - 2008. - кн. 37. – С. 963-969.

Една от неотложните задачи на съвременната навигация на безпилотни летателни апарати (БЛА) е задачата за повишаване на точността на определяне на координатите. Този проблем се решава чрез използване на различни опции за интегриране на навигационни системи. Един от съвременните варианти на интеграция е комбинацията от gps/glonass навигация с разширен филтър на Калман (Extended Kalmanfilter), рекурсивно оценяващ точността, използвайки непълни и шумни измервания. В момента съществуват и се разработват различни варианти на разширения филтър на Калман, включително разнообразен брой променливи на състоянието. В тази работа ще покажем колко ефективно може да бъде използването му в съвременните разработки. Нека разгледаме едно от характерните представяния на такъв филтър.

Изграждане на математически модел

AT този примерще говорим само за движението на UAV в хоризонталната равнина, в противен случай ще разгледаме така наречения 2d проблем за локализация. В нашия случай това е оправдано от факта, че за много практически възникнали ситуации БПЛА може да остане приблизително на същата височина. Това предположение се използва широко за опростяване на моделирането на динамиката на самолета. Динамичният модел на UAV е даден от следната система от уравнения:

където () - координатите на UAV в хоризонталната равнина като функция на времето, посоката на UAV, ъгловата скорост на UAV и v земната скорост на UAV, функции и ще се считат за постоянни. Те са взаимно независими, с известни ковариации и , равни съответно на и и се използват за симулиране на промени в ускорението на UAV, причинени от вятър, маневри на пилота и др. Стойностите и са получени от максималната ъглова скорост на UAV и експерименталните стойности на промените в линейната скорост на UAV, - символът на Kronecker.

Тази система от уравнения ще бъде приблизителна поради нелинейността в модела и поради наличието на шум. Най-простото приближение в този случай е приближението на Ойлер. Дискретният модел на системата за динамично движение на UAV е показан по-долу.

дискретен вектор на състоянието на филтъра на Калман, който позволява апроксимиране на стойността на непрекъснат вектор на състоянието. ∆ - интервал от време между k и k+1 измервания. () и () - последователности от стойности на бял шум на Гаус с нулева средна стойност. Ковариационна матрица за първата последователност:

По същия начин за втората последователност:

След като направим съответните замествания в уравненията на системата (2), получаваме:

Последователностите и са взаимно независими. Те също са нулеви средни бели гаусови шумови последователности с ковариационни матрици и съответно. Предимството на тази форма е, че показва промяната в дискретния шум между всяко измерване. В резултат на това получаваме следния дискретен динамичен модел:

(3)

Уравнение за:

= + , (4)

където x и y са координатите на UAV в k-времевата точка и е Гаусова последователност от случайни параметри с нулева средна стойност, която се използва за определяне на грешката. Предполага се, че тази последователност е независима от () и ().

Изрази (3) и (4) служат като основа за оценка на местоположението на UAV, където k-ти координатиполучени с помощта на разширения филтър на Калман. Моделиране на отказ на навигационни системи във връзка с този видфилтър показва своята значителна ефективност.

За по-голяма яснота даваме малък прост пример. Нека някой UAV лети равномерно, с известно постоянно ускорение a.

Където x е координатата на UAV в t-времето, а δ е някаква случайна променлива.

Да предположим, че имаме gps сензор, който получава данни за местоположението на самолет. Нека представим резултата от моделирането на този процес в софтуерния пакет MATLAB.

Ориз. 1. Филтриране на показанията на сензора с помощта на филтъра на Калман

На фиг. 1 показва колко ефективно може да бъде използването на филтрирането на Калман.

В реална ситуация обаче сигналите често имат нелинейна динамика и необичаен шум. Именно в такива случаи се използва разширеният филтър на Калман. В случай, че дисперсиите на шума не са твърде големи (т.е. линейното приближение е адекватно), прилагането на разширения филтър на Калман дава решение на проблема с висока точност. Въпреки това, когато шумът не е Гаус, разширеният филтър на Калман не може да бъде приложен. В този случай обикновено се използва частичен филтър, който използва числени методи за вземане на интеграли, базирани на методите на Монте Карло с вериги на Марков.

Филтър за частици

Нека си представим един от алгоритмите, които развиват идеите на разширения филтър на Калман - частичен филтър. Частичното филтриране е неоптимален метод за филтриране, който работи, когато се извършва комбиниране на Монте Карло върху набор от частици, които представляват вероятностното разпределение на процеса. Тук частицата е елемент, взет от предварителното разпределение на оценения параметър. Основната идея на частичния филтър е, че голям брой частици могат да бъдат използвани за представяне на оценка на разпределението. Колкото по-голям е броят на използваните частици, толкова по-точно наборът от частици ще представлява предишното разпределение. Филтърът за частици се инициализира чрез поставяне на N частици в него от предварителното разпределение на параметрите, които искаме да оценим. Алгоритъмът за филтриране предполага, че тези частици преминават специална система, и след това претегляне с помощта на информацията, получена от измерването на тези частици. Получените частици и свързаните с тях маси представляват задното разпределение на процеса на оценка. Цикълът се повтаря за всяко ново измерване и теглата на частиците се актуализират, за да представят последващото разпределение. Един от основните проблеми с традиционния подход за филтриране на частици е, че резултатът обикновено е няколко частици, които са много тежки, за разлика от повечето други, които са много леки. Това води до нестабилност на филтрирането. Този проблем може да бъде решен чрез въвеждане на честота на дискретизация, при която N нови частици се вземат от разпределение, съставено от стари частици. Резултатът от оценката се получава чрез получаване на проба от средната стойност на множеството частици. Ако имаме множество независими проби, тогава средната стойност на извадката ще бъде точна оценка на средната стойност, определяща крайната дисперсия.

Дори ако филтърът за частици не е оптимален, тогава тъй като броят на частиците клони към безкрайност, ефективността на алгоритъма се доближава до байесовото правило за оценка. Затова е желателно да има възможно най-много частици, за да се получи най-добър резултат. За съжаление това води до силно увеличаване на сложността на изчисленията и следователно налага търсенето на компромис между точност и скорост на изчисление. Така че броят на частиците трябва да бъде избран въз основа на изискванията за проблема за оценка на точността. Друг важен фактор за работата на филтъра за частици е ограничението на честотата на вземане на проби. Както бе споменато по-рано, честотата на дискретизация е важен параметър за филтриране на частици и без нея алгоритъмът в крайна сметка ще се изроди. Идеята е, че ако теглата са разпределени твърде неравномерно и прагът за вземане на проби скоро бъде достигнат, тогава частиците с ниско тегло се изхвърлят, а останалият набор формира нова плътност на вероятността, за която могат да бъдат взети нови проби. Изборът на прага на честотата на дискретизация е доста трудна задача, защото също висока честотакара филтъра да бъде твърде чувствителен към шум, а твърде ниската дава голяма грешка. Друг важен фактор е плътността на вероятността.

Като цяло алгоритъмът за филтриране на частици показва добра производителност при позициониране за неподвижни цели и за относително бавно движещи се цели с неизвестна динамика на ускорението. Като цяло алгоритъмът за филтриране на частици е по-стабилен от разширения филтър на Калман и е по-малко склонен към дегенерация и тежки проблеми. В случаи на нелинейно, негаусово разпределение този алгоритъмфилтрирането показва много добра точност на местоположението на целта, докато разширеният алгоритъм за филтриране на Калман не може да се използва при такива условия. Недостатъците на този подход включват неговата по-висока сложност в сравнение с разширения филтър на Калман, както и факта, че не винаги е очевидно как да се изберат правилните параметри за този алгоритъм.

Обещаващи изследвания в тази област

Използването на филтърен модел на Калман, подобен на този, който дадохме, може да се види в , където се използва за подобряване на производителността на интегрирана система (GPS + модел за компютърно зрение за съпоставяне с географска база) и ситуацията на повреда на сателитно навигационно оборудване също се симулира. С помощта на филтъра на Калман резултатите от работата на системата в случай на повреда бяха значително подобрени (например грешката при определяне на височината беше намалена около два пъти и грешките при определяне на координатите по различни оси бяха намалени почти 9 пъти). Подобно използване на филтъра на Калман също е дадено в .

Интересен проблем от гледна точка на набор от методи е решен в . Той също така използва филтър на Калман с 5 състояния, с някои разлики в изграждането на модела. Полученият резултат надвишава резултата от нашия модел поради използването на допълнителни средства за интеграция (използвани са фото и термични изображения). Прилагането на филтъра на Калман в този случай позволява да се намали грешката при определяне на пространствените координати на дадена точка до стойност от 5,5 m.

Заключение

В заключение отбелязваме, че използването на филтъра на Калман в системите за позициониране на UAV се практикува в много съвременни разработки. Има огромен брой вариации и аспекти на тази употреба, до едновременното използване на няколко подобни филтъра с различни коефициенти на състояние. Една от най-обещаващите области за развитие на филтрите на Калман е работата по създаването на модифициран филтър, чиито грешки ще бъдат представени от цветен шум, което ще го направи още по-ценен за решаване на реални проблеми. Също така от голям интерес в областта на изкуството е частичен филтър, с който може да се филтрира негаусов шум. Това разнообразие и осезаемите резултати при подобряване на точността, особено в случай на повреда на стандартните сателитни навигационни системи, са основните фактори, влияещи върху тази технология в различни научни области, свързани с разработването на точни и устойчиви на грешки навигационни системи за различни летателни апарати.

Рецензенти:

Лабунец В. Г., доктор на техническите науки, професор, професор в катедрата теоретични основиРадиотехнически Уралски федерален университет, кръстен на първия президент на Русия B.N. Елцин, Екатеринбург;

Иванов В. Е., доктор на техническите науки, професор, ръководител. Катедра по технологии и комуникации, Уралски федерален университет, кръстен на първия президент на Русия Б.Н. Елцин, Екатеринбург.

Библиографска връзка

Random Forest е един от любимите ми алгоритми за извличане на данни. Първо, той е невероятно гъвкав, може да се използва за решаване както на проблеми с регресия, така и на класификация. Търсете аномалии и изберете предиктори. Второ, това е алгоритъм, който наистина е трудно да се приложи неправилно. Просто защото, за разлика от други алгоритми, има малко персонализирани параметри. И въпреки това е изненадващо проста в същността си. В същото време е забележително точен.

Каква е идеята на такъв прекрасен алгоритъм? Идеята е проста: да кажем, че имаме много слаб алгоритъм, да речем. Ако направим много различни модели, използвайки този слаб алгоритъм и осредним резултата от техните прогнози, тогава крайният резултат ще бъде много по-добър. Това е така нареченото ансамбълно обучение в действие. Алгоритъмът Random Forest следователно се нарича "Random Forest", за получените данни той създава много дървета на решения и след това осреднява резултата от техните прогнози. Важен момент тук е елементът на произволност при създаването на всяко дърво. В крайна сметка е ясно, че ако създадем много еднакви дървета, тогава резултатът от тяхното осредняване ще има точността на едно дърво.

Как работи той? Да предположим, че имаме някои входни данни. Всяка колона съответства на някакъв параметър, всеки ред съответства на някакъв елемент от данни.

Можем да изберем произволно редица колони и редове от целия набор от данни и да изградим дърво на решенията от тях.

Четвъртък, 10 май 2012 г

Четвъртък, 12 януари 2012 г

Всичко започна през април 2011 г., когато имах телефонно интервю със Zynga. Тогава всичко изглеждаше като някаква игра, която нямаше нищо общо с реалността и дори не можех да си представя до какво ще доведе. През юни 2011 г. Zynga пристигна в Москва и проведе серия от интервюта, бяха разгледани около 60 кандидати, преминали телефонно интервю, и около 15 души бяха избрани от тях (не знам точния брой, някой промени решението си по-късно, някой веднага отказа). Интервюто се оказа учудващо просто. Няма задачи за програмиране за вас, няма сложни въпроси относно формата на люкове, тества се главно способността за чат. А знанията според мен се оценяваха само повърхностно.

И тогава започна манипулацията. Първо изчакахме резултатите, след това офертата, след това одобрението на LCA, след това одобрението на молбата за виза, след това документите от САЩ, след това опашката в посолството, след това допълнителната проверка, след това визата. На моменти ми се струваше, че съм готов да зарежа всичко и да вкарам. На моменти се съмнявах дали ни трябва тази Америка, защото и Русия не е лоша. Целият процес отне около половин година, в крайна сметка в средата на декември получихме визи и започнахме да се подготвяме за заминаване.

Понеделник беше първият ми ден на новата работа. Офисът разполага с всички условия не само за работа, но и за живеене. Закуски, обеди и вечери от нашите собствени готвачи, куп разнообразна храна, натъпкана във всички ъгли, фитнес зала, масаж и дори фризьор. Всичко това е напълно безплатно за служителите. Много от тях стигат до работа с колело, а няколко стаи са оборудвани за съхранение на превозни средства. Като цяло, никога не съм виждал нещо подобно в Русия. Всичко обаче си има цена, веднага ни предупредиха, че ще трябва да работим много. Какво е "много", по техните стандарти, не ми е много ясно.

Надявам се обаче, че въпреки многото работа, в обозримо бъдеще ще мога да възобновя блоговете и може би ще разкажа нещо за американския живот и работата като програмист в Америка. Изчакай и виж. Междувременно желая на всички ви Весела Коледа и Щастлива Нова година и до скоро!

резултат<- NULL for(i in (1:length(divs[,1]))){ d <- divs if (d$Divs>0)( опитай(( кавички<- getSymbols(d$Symbol, src="Finam", from="2010-01-01", auto.assign=FALSE) if (!is.nan(quotes)){ price <- Cl(quotes) if (length(price)>0)(dd<- d$Divs result <- rbind(result, data.frame(d$Symbol, d$Name, d$RegistryDate, as.numeric(dd)/as.numeric(price), stringsAsFactors=FALSE)) } } }, silent=TRUE) } } colnames(result) <- c("Symbol", "Name", "RegistryDate", "Divs") result

В интернет, включително Habré, можете да намерите много информация за филтъра на Калман. Но е трудно да се намери лесно смилаема производна на самите формули. Без заключение цялата тази наука се възприема като вид шаманизъм, формулите изглеждат като безличен набор от символи и най-важното е, че много прости твърдения, които лежат на повърхността на теорията, са извън разбирането. Целта на тази статия ще бъде да говорим за този филтър на възможно най-достъпен език.
Филтърът на Калман е мощен инструмент за филтриране на данни. Основният му принцип е, че при филтриране се използва информация за физиката на самото явление. Да кажем, че ако филтрирате данни от скоростомера на автомобил, тогава инерцията на автомобила ви дава правото да възприемате твърде бързите скокове на скоростта като грешка в измерването. Филтърът на Калман е интересен, защото в известен смисъл е най-добрият филтър. По-долу ще разгледаме по-подробно какво точно означават думите „най-доброто“. В края на статията ще покажа, че в много случаи формулите могат да бъдат опростени до такава степен, че от тях да не остане почти нищо.

Ликбез

Преди да се запознаем с филтъра на Калман, предлагам да си припомним някои прости дефиниции и факти от теорията на вероятностите.

Случайна стойност

Когато казват, че е дадена случайна променлива, те имат предвид, че тази променлива може да приема случайни стойности. Приема различни стойности с различни вероятности. Когато хвърлите, да речем, зар, ще падне дискретен набор от стойности: . Когато става въпрос, например, за скоростта на блуждаеща частица, тогава очевидно трябва да се работи с непрекъснат набор от стойности. „Отпадналите“ стойности на случайна променлива ще бъдат обозначени с , но понякога ще използваме същата буква, която обозначава случайна променлива: .
В случай на непрекъснат набор от стойности, случайната променлива се характеризира с плътността на вероятността , която ни диктува, че вероятността случайната променлива да "изпадне" в малък квартал на точка с дължина е равна на . Както можем да видим от снимката, тази вероятност е равна на площта на защрихования правоъгълник под графиката:

Доста често в живота случайните променливи се разпределят според Гаус, когато плътността на вероятността е .

Виждаме, че функцията има формата на камбана, центрирана в точка и с характерна ширина от порядъка на .
Тъй като говорим за разпределението на Гаус, ще бъде грехота да не споменем откъде идва. Точно както числата са твърдо установени в математиката и се появяват на най-неочаквани места, така разпределението на Гаус е пуснало дълбоки корени в теорията на вероятностите. Едно забележително твърдение, което частично обяснява вездесъщността на Гаус, е следното:
Нека има случайна променлива с произволно разпределение (всъщност има някои ограничения за този произвол, но те не са никак твърди). Нека проведем експерименти и изчислим сумата от "отпадналите" стойности на случайна променлива. Нека направим много от тези експерименти. Ясно е, че всеки път ще получаваме различна стойност на сумата. С други думи, тази сума сама по себе си е случайна променлива със свой определен закон на разпределение. Оказва се, че за достатъчно големи, законът за разпределение на тази сума клони към разпределението на Гаус (между другото, характерната ширина на „камбаната“ нараства като ). Прочетете повече в wikipedia: централна гранична теорема. В живота много често има количества, които са съставени от голям брой еднакво разпределени независими случайни променливи и следователно са разпределени според Гаус.

Означава

Средната стойност на случайна променлива е това, което получаваме в границата, ако проведем много експерименти и изчислим средноаритметичната стойност на изпуснатите стойности. Средната стойност се обозначава по различни начини: математиците обичат да обозначават с (очакване), а чуждестранните математици с (очакване). Физика същото чрез или. Ще обозначим по чужд начин:.
Например за разпределение на Гаус средната стойност е .

дисперсия

В случая на разпределението на Гаус можем ясно да видим, че случайната променлива предпочита да изпадне в някаква близост на средната си стойност. Както може да се види от графиката, характерното разсейване на стойностите на поръчката е . Как можем да оценим това разпространение на стойности за произволна случайна променлива, ако знаем нейното разпределение. Можете да начертаете графика на неговата плътност на вероятността и да оцените характерната ширина на око. Но ние предпочитаме да вървим по алгебричния път. Можете да намерите средната дължина на отклонението (модула) от средната стойност: . Тази стойност ще бъде добра оценка на характерното разпространение на стойностите. Но вие и аз знаем много добре, че използването на модули във формули е главоболие, така че тази формула рядко се използва за оценка на характерното разпространение.
По-лесен начин (прост от гледна точка на изчисления) е да се намери . Това количество се нарича дисперсия и често се нарича . Коренът на дисперсията се нарича стандартно отклонение. Стандартното отклонение е добра оценка на разпространението на случайна променлива.
Например, за гаусово разпределение можем да приемем, че дисперсията, дефинирана по-горе, е точно равна на , което означава, че стандартното отклонение е равно на , което се съгласува много добре с нашата геометрична интуиция.
Всъщност тук се крие малка измама. Факт е, че в дефиницията на разпределението на Гаус под показателя е изразът . Това две в знаменателя е точно така, че стандартното отклонение да е равно на коефициента. Тоест, самата формула за разпределение на Гаус е написана във форма, специално изострена за факта, че ще вземем предвид нейното стандартно отклонение.

Независими случайни променливи

Случайните променливи могат или не могат да бъдат зависими. Представете си, че хвърляте игла върху самолет и записвате координатите на двата му края. Тези две координати са зависими, те са свързани с условието, че разстоянието между тях винаги е равно на дължината на иглата, въпреки че са случайни величини.
Случайните променливи са независими, ако резултатът от първата е напълно независим от резултата от втората. Ако случайните променливи и са независими, тогава средната стойност на техния продукт е равна на произведението на техните средни стойности:

Доказателство

Например сините очи и завършването на училище със златен медал са независими случайни променливи. Ако синеоки, да речем златни медалисти , тогава синеоки медалисти Този пример ни казва, че ако случайните променливи и са дадени от техните вероятностни плътности и , тогава независимостта на тези количества се изразява във факта, че вероятностната плътност (първата отпадна стойност , а второто ) се намира по формулата:

От това веднага следва, че:

Както можете да видите, доказателството се извършва за случайни променливи, които имат непрекъснат спектър от стойности и са дадени от тяхната плътност на вероятността. В други случаи идеята за доказателство е подобна.

Калман филтър

Формулиране на проблема

Означаваме със стойността, която ще измерим и след това филтрираме. Тя може да бъде координата, скорост, ускорение, влажност, степен на воня, температура, налягане и др.
Нека започнем с прост пример, който ще ни отведе до формулирането на общ проблем. Представете си, че имаме радиоуправляема кола, която може да се движи само напред и назад. Ние, знаейки теглото на автомобила, формата, пътната настилка и т.н., изчислихме как управляващият джойстик влияе върху скоростта на движение.

Тогава координатата на машината ще се промени според закона:

В реалния живот не можем да вземем предвид в нашите изчисления малки смущения, действащи върху автомобила (вятър, неравности, камъчета по пътя), така че реалната скорост на автомобила ще се различава от изчислената. Случайна променлива се добавя към дясната страна на писменото уравнение:

Имаме монтиран GPS сензор на колата, който се опитва да измери истинската координата на колата и, разбира се, не може да я измери точно, но я измерва с грешка, която също е случайна величина. В резултат на това получаваме грешни данни от сензора:

Проблемът е, че като знаете неправилните показания на сензора, намерете добро приближение за истинската координата на машината.
При формулирането на общия проблем всичко може да бъде отговорно за координатата (температура, влажност ...), а терминът, отговорен за управлението на системата отвън, ще обозначим като (в примера с машината). Уравненията за координатите и показанията на сензора ще изглеждат така:

Нека обсъдим подробно това, което знаем:

Полезно е да се отбележи, че задачата за филтриране не е задача за изглаждане. Ние не се стремим да изгладим данните от сензора, ние се стремим да получим най-близката стойност до реалната координата.

Алгоритъм на Калман

Ще разсъждаваме по индукция. Представете си, че на -тата стъпка вече сме намерили филтрираната стойност от сензора, която се доближава добре до истинската координата на системата. Не забравяйте, че знаем уравнението, което контролира промяната в неизвестна координата:

следователно, без все още да получим стойността от сензора, можем да предположим, че на стъпката системата се развива според този закон и сензорът ще покаже нещо близко до . За съжаление все още не можем да кажем нищо по-точно. От друга страна, на стъпалото ще имаме неточно показание на сензора на ръцете.
Идеята на Калман е следната. За да получим най-доброто приближение до истинската координата, трябва да изберем благоприятна среда между неточното отчитане на сензора и нашата прогноза за това, което очакваме да видим. Ще дадем тегло на показанията на сензора и прогнозираната стойност ще има тегло:

Коефициентът се нарича коефициент на Калман. Зависи от стъпката на итерация, така че би било по-правилно да напишем, но засега, за да не претрупваме формулите за изчисление, ще пропуснем неговия индекс.
Трябва да изберем коефициента на Калман по такъв начин, че получената оптимална стойност на координатата да бъде най-близо до истинската стойност. Например, ако знаем, че нашият сензор е много точен, тогава ще се доверим повече на показанията му и ще придадем на стойността по-голяма тежест (близо до единица). Ако сензорът, напротив, изобщо не е точен, тогава ще се съсредоточим повече върху теоретично прогнозираната стойност на .
Като цяло, за да се намери точната стойност на коефициента на Калман, просто трябва да се минимизира грешката:

Използваме уравнения (1) (тези в синята кутия), за да пренапишем израза за грешката:

Доказателство

Сега е моментът да обсъдим какво означава изразът минимизиране на грешката? В крайна сметка грешката, както виждаме, сама по себе си е случайна променлива и всеки път приема различни стойности. Наистина няма универсален подход за определяне на това какво означава грешката да бъде минимална. Точно както в случая с дисперсията на случайна променлива, когато се опитахме да оценим характерната ширина на нейното разсейване, тук ще изберем най-простия критерий за изчисления. Ще минимизираме средната стойност от грешката на квадрат:

Нека напишем последния израз:

Доказателство

От факта, че всички случайни променливи, включени в израза за са независими, следва, че всички "кръстосани" членове са равни на нула:

Използвахме факта, че , тогава формулата за дисперсията изглежда много по-проста: .

Този израз приема минимална стойност, когато (приравнете производната на нула):

Тук вече пишем израз за коефициента на Калман с индекс на стъпка, като по този начин подчертаваме, че зависи от стъпката на итерация.
Заместваме получената оптимална стойност в израза, за който сме минимизирали. Получаваме;

Нашата задача е решена. Получихме итеративна формула за изчисляване на коефициента на Калман.
Нека обобщим придобитите знания в една рамка:

Пример

Код на Matlab

изчисти всичко; N=100% брой проби a=0,1% ускорение sigmaPsi=1 sigmaEta=50; k=1:N x=k x(1)=0 z(1)=x(1)+normrnd(0,sigmaEta); за t=1:(N-1) x(t+1)=x(t)+a*t+normrnd(0,sigmaPsi); z(t+1)=x(t+1)+normrnd(0,sigmaEta); край; %калман филтър xOpt(1)=z(1); eOpt(1)=sigmaEta; за t=1:(N-1) eOpt(t+1)=sqrt((sigmaEta^2)*(eOpt(t)^2+sigmaPsi^2)/(sigmaEta^2+eOpt(t)^2+ sigmaPsi^2)) K(t+1)=(eOpt(t+1))^2/sigmaEta^2 xOpt(t+1)=(xOpt(t)+a*t)*(1-K(t +1))+K(t+1)*z(t+1) край; plot(k,xopt,k,z,k,x)

Анализ

Ако проследим как се променя коефициентът на Калман със стъпката на итерация, тогава можем да покажем, че той винаги се стабилизира до определена стойност. Например, когато RMS грешките на сензора и модела се отнасят една към друга като десет към едно, тогава графиката на коефициента на Калман в зависимост от стъпката на итерация изглежда така:

В следващия пример ще обсъдим как това може да направи живота ни много по-лесен.

Втори пример

На практика често се случва да не знаем абсолютно нищо за физическия модел на това, което филтрираме. Например искате да филтрирате показанията от любимия си акселерометър. Не знаете предварително по какъв закон възнамерявате да завъртите акселерометъра. Най-много информация, която можете да съберете, е дисперсията на грешката на сензора. В такава трудна ситуация, цялото непознаване на модела на движение може да се превърне в случайна променлива:

Но, честно казано, такава система вече не отговаря на условията, които наложихме на случайната променлива, защото сега цялата непозната за нас физика на движението е скрита там и следователно не можем да кажем, че в различни моменти от време грешките на модела са независими един от друг и че техните средни стойности са нула. В този случай като цяло теорията на филтъра на Калман е неприложима. Но няма да обръщаме внимание на този факт, а глупаво прилагаме целия колос от формули, избирайки коефициентите и на око, така че филтрираните данни да изглеждат добре.
Но има и друг, много по-лесен начин. Както видяхме по-горе, коефициентът на Калман винаги се стабилизира до стойността . Следователно, вместо да избираме коефициентите и да намираме коефициента на Калман с помощта на сложни формули, можем да считаме този коефициент за винаги константа и да избираме само тази константа. Това предположение няма да развали почти нищо. Първо, ние вече незаконно използваме теорията на Калман, и второ, коефициентът на Калман бързо се стабилизира до константа. В крайна сметка всичко ще бъде много просто. Изобщо не се нуждаем от формули от теорията на Калман, просто трябва да изберем приемлива стойност и да я вмъкнем в итеративната формула:

Следващата графика показва данни от фиктивен сензор, филтрирани по два различни начина. При условие, че не знаем нищо за физиката на явлението. Първият начин е честен, с всички формули от теорията на Калман. А вторият е опростен, без формули.

Както виждаме, методите са почти еднакви. Малка разлика се наблюдава само в началото, когато коефициентът на Калман все още не се е стабилизирал.

Дискусия

Както видяхме, основната идея на филтъра на Калман е да се намери такъв коефициент, че филтрираната стойност

средно ще се различава най-малко от реалната стойност на координатата. Виждаме, че филтрираната стойност е линейна функция на показанията на сензора и предишната филтрирана стойност. А предишната филтрирана стойност от своя страна е линейна функция на показанията на сензора и предишната филтрирана стойност. И така, докато веригата се разгъне напълно. Тоест филтрираната стойност зависи от всичкопредишни показания на сензора линейно:

Следователно филтърът на Калман се нарича линеен филтър.
Може да се докаже, че филтърът на Калман е най-добрият от всички линейни филтри. Най-доброто в смисъл, че средният квадрат на грешката на филтъра е минимален.

Многовариантен случай

Цялата теория на филтъра на Калман може да се обобщи за многоизмерния случай. Формулите там изглеждат малко по-страшни, но самата идея за извеждането им е същата като в едномерния случай. Можете да ги видите в тази страхотна статия: http://habrahabr.ru/post/140274/ .
И в това прекрасно видеопример за това как да ги използвате.