Säkerhetsinformationsportal. Kalman filtrering Kalman filter för skalära mätningar

Wienerfilter är bäst lämpade för bearbetning av processer eller segment av processer som helhet (blockbearbetning). Sekventiell bearbetning kräver en aktuell uppskattning av signalen vid varje cykel, med hänsyn tagen till informationen som tas emot vid filteringången under observationsprocessen.

Med Wiener-filtrering skulle varje nytt signalprov kräva omräkning av alla filtervikter. För närvarande används adaptiva filter i stor utsträckning, där inkommande ny information används för kontinuerlig korrigering av den tidigare gjorda signalutvärderingen (målföljning i radar, automatiska styrsystem i styrning, etc.). Av särskilt intresse är adaptiva filter av den rekursiva typen, kända som Kalman-filtret.

Dessa filter används i stor utsträckning i styrslingor i automatiska regler- och styrsystem. Det är där de kom ifrån, vilket framgår av en sådan specifik terminologi som används för att beskriva deras arbete som det statliga rummet.

En av huvuduppgifterna som måste lösas vid utövandet av neurala datorer är att få snabba och pålitliga inlärningsalgoritmer för neurala nätverk. I detta avseende kan det vara användbart att använda en inlärningsalgoritm av linjära filter i återkopplingsslingan. Eftersom inlärningsalgoritmer är iterativa till sin natur måste ett sådant filter vara en sekventiell rekursiv estimator.

Problem med parameteruppskattning

Ett av problemen med teorin om statistiska lösningar, som är av stor praktisk betydelse, är problemet med att uppskatta systemens tillståndsvektorer och parametrar, vilket är formulerat enligt följande. Antag att det är nödvändigt att uppskatta värdet på vektorparametern $X$, som är otillgänglig för direkt mätning. Istället mäts en annan parameter $Z$, beroende på $X$. Uppskattningens uppgift är att svara på frågan: vad kan man säga om $X$ givet $Z$. I det allmänna fallet beror proceduren för optimal uppskattning av vektorn $X$ på det accepterade kvalitetskriteriet för uppskattningen.

Till exempel kräver den bayesianska metoden för parameteruppskattningsproblemet fullständig a priori-information om de probabilistiska egenskaperna hos den uppskattade parametern, vilket ofta är omöjligt. I dessa fall tillgriper man metoden med minsta kvadrater (LSM), som kräver mycket mindre a priori-information.

Låt oss överväga tillämpningen av minsta kvadrater för det fall då observationsvektorn $Z$ är kopplad till parameteruppskattningsvektorn $X$ genom en linjär modell, och det finns ett brus $V$ i observationen som inte är korrelerad med uppskattad parameter:

$Z = HX + V$, (1)

där $H$ är transformationsmatrisen som beskriver förhållandet mellan de observerade värdena och de uppskattade parametrarna.

Uppskattningen $X$ som minimerar det kvadratiska felet skrivs enligt följande:

$X_(ots)=(H^TR_V^(-1)H)^(-1)H^TR_V^(-1)Z$, (2)

Låt bruset $V$ vara okorrelerat, i vilket fall matrisen $R_V$ bara är identitetsmatrisen, och uppskattningsekvationen blir enklare:

$X_(ots)=(H^TH)^(-1)H^TZ$, (3)

Att spela in i matrisform sparar mycket papper, men kan vara ovanligt för någon. Följande exempel, hämtat från Yu. M. Korshunovs monografi "Mathematical Foundations of Cybernetics", illustrerar allt detta.
Det finns följande elektriska krets:

De observerade värdena i detta fall är instrumentavläsningarna $A_1 ​​= 1 A, A_2 = 2 A, V = 20 B$.

Dessutom är motståndet $R = 5$ Ohm känt. Det krävs att man på bästa sätt uppskattar värdena för strömmarna $I_1$ och $I_2$, utifrån det minsta medelkvadratfelskriteriet. Det viktigaste här är att det finns ett visst samband mellan de observerade värdena (instrumentavläsningar) och de uppskattade parametrarna. Och denna information hämtas utifrån.

I det här fallet är det Kirchhoffs lagar, i fallet med filtrering (vilket kommer att diskuteras senare) - en autoregressiv tidsseriemodell, som antar att det aktuella värdet beror på de tidigare.

Så, kunskap om Kirchhoffs lagar, som inte på något sätt är kopplad till teorin om statistiska beslut, gör att du kan upprätta en koppling mellan de observerade värdena och de uppskattade parametrarna (de som studerade elektroteknik kan kontrollera, resten måste ta deras ord för det):

$$z_1 = A_1 = I_1 + \xi_1 = 1$$

$$z_2 = A_2 = I_1 + I_2 + \xi_2 = 2$$

$$z_2 = V/R = I_1 + 2 * I_2 + \xi_3 = 4$$

Detta är i vektorform:

$$\begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) \begin(vmatrix) I_1\ \ I_2 \end(vmatrix) + \begin(vmatrix) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrix)$$

Eller $Z = HX + V$, där

$$Z= \begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1\\ 2\\ 4 \end(vmatrix) ; H= \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) ; X= \begin(vmatrix) I_1\\ I_2 \end(vmatrix) ; V= \begin(vmatrix) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrix)$$

Med tanke på brusvärdena som okorrelerade med varandra hittar vi uppskattningen av I 1 och I 2 med minsta kvadratmetoden i enlighet med formel 3:

$H^TH= \begin(vmatrix) 1 & 1& 1\\ 0 & 1& 2 \end(vmatrix) \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) = \ begin(vmatrix) 3 & 3\\ 3 & 5 \end(vmatrix) ; (H^TH)^(-1)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) $;

$H^TZ= \begin(vmatrix) 1 & 1& 1\\ 0 & 1& 2 \end(vmatrix) \begin(vmatrix) 1 \\ 2\\ 4 \end(vmatrix) = \begin(vmatrix) 7\ \ 10 \end(vmatris) ; X(vmatrix)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) \begin(vmatrix) 7\\ 10 \end(vmatrix) = \frac (1)(6) \begin(vmatrix) 5\\ 9 \end(vmatrix)$;

Så $I_1 = 5/6 = 0,833 A$; $I_2 = 9/6 = 1,5 A$.

Filtreringsuppgift

Till skillnad från uppgiften att uppskatta parametrar som har fasta värden, krävs det i filtreringsproblemet att utvärdera processer, det vill säga att hitta aktuella uppskattningar av en tidsvarierande signal som är förvrängd av brus och därför otillgänglig för direkt mätning. I det allmänna fallet beror typen av filtreringsalgoritmer på de statistiska egenskaperna hos signalen och bruset.

Vi kommer att anta att den användbara signalen är en långsamt varierande funktion av tiden, och att bruset är okorrelerat brus. Vi kommer att använda minsta kvadratmetoden, återigen på grund av bristen på a priori-information om de probabilistiska egenskaperna hos signalen och bruset.

Först får vi en uppskattning av det aktuella värdet av $x_n$ med de sista $k$-värdena i tidsserien $z_n, z_(n-1),z_(n-2)\dots z_(n-( k-1))$. Observationsmodellen är densamma som i parameteruppskattningsproblemet:

Det är tydligt att $Z$ är en kolumnvektor som består av de observerade värdena av tidsserierna $z_n, z_(n-1),z_(n-2)\dots z_(n-(k-1)) $, $V $ – bruskolumnvektor $\xi _n, \xi _(n-1),\xi_(n-2)\dots \xi_(n-(k-1))$, förvränger den sanna signalen. Och vad betyder symbolerna $H$ och $X$? Vilken typ av kolumnvektor $X$ kan vi till exempel prata om om det enda som behövs är att ge en uppskattning av tidsseriens aktuella värde? Och vad som menas med transformationsmatrisen $H$ är inte alls klart.

Alla dessa frågor kan endast besvaras om konceptet med en signalgenereringsmodell införs i övervägande. Det vill säga, någon modell av den ursprungliga signalen behövs. Detta är förståeligt, i frånvaro av a priori information om de probabilistiska egenskaperna hos signalen och bruset återstår det bara att göra antaganden. Man kan kalla det spådomar på kaffesumpen, men experter föredrar en annan terminologi. I deras hårtork kallas detta en parametrisk modell.

I det här fallet utvärderas parametrarna för just denna modell. När du väljer en lämplig signalgenereringsmodell, kom ihåg att alla analytiska funktioner kan utökas i en Taylor-serie. En slående egenskap hos Taylor-serien är att formen av en funktion på valfritt ändligt avstånd $t$ från någon punkt $x=a$ bestäms unikt av funktionens beteende i en oändligt liten omgivning av punkten $x=a $ (vi talar om dess första och högre ordningens derivator).

Således innebär förekomsten av Taylor-serier att den analytiska funktionen har en intern struktur med en mycket stark koppling. Om vi ​​till exempel begränsar oss till tre medlemmar av Taylor-serien, kommer signalgenereringsmodellen att se ut så här:

$x_(n-i) = F_(-i)x_n$, (4)

$$X_n= \begin(vmatrix) x_n\\ x"_n\\ x""_n \end(vmatrix) ; F_(-i)= \begin(vmatrix) 1 & -i & i^2/2\\ 0 & 1 & -i\\ 0 & 0 & 1 \end(vmatrix) $$

Det vill säga, formel 4, med en given ordning av polynomet (i exemplet är det lika med 2), upprättar en koppling mellan $n$-th-värdet för signalen i tidssekvensen och $(n-i)$-th . Således inkluderar den uppskattade tillståndsvektorn i detta fall, förutom själva det uppskattade värdet, signalens första och andra derivata.

I teorin om automatisk styrning skulle ett sådant filter kallas ett andra ordningens astatiskt filter. Transformationsmatrisen $H$ för det här fallet (uppskattningen är baserad på nuvarande och $k-1$ tidigare prov) ser ut så här:

$$H= \begin(vmatrix) 1 & -k & k^2/2\\ - & - & -\\ 1 & -2 & 2\\ 1 & -1 & 0.5\\ 1 & 0 & 0 \ end(vmatrix)$$

Alla dessa siffror erhålls från Taylor-serien, förutsatt att tidsintervallet mellan angränsande observerade värden är konstant och lika med 1.

Således har filtreringsproblemet, under våra antaganden, reducerats till problemet med att uppskatta parametrar; i detta fall uppskattas parametrarna för signalgenereringsmodellen som antagits av oss. Och utvärderingen av värdena för tillståndsvektorn $X$ utförs enligt samma formel 3:

$$X_(ots)=(H^TH)^(-1)H^TZ$$

Faktum är att vi har implementerat en parametrisk uppskattningsprocess baserad på en autoregressiv modell av signalgenereringsprocessen.

Formel 3 är lätt att implementera i mjukvara, för detta måste du fylla i matrisen $H$ och vektorkolumnen för observationer $Z$. Sådana filter kallas ändliga minnesfilter, eftersom de använder de senaste $k$-observationerna för att få den aktuella skattningen $X_(not)$. Vid varje nytt observationssteg läggs en ny uppsättning observationer till den nuvarande uppsättningen av observationer och den gamla kasseras. Denna utvärderingsprocess kallas glidande fönster.

Växande minnesfilter

Filter med ändligt minne har den största nackdelen att efter varje ny observation är det nödvändigt att räkna om en fullständig omräkning av all data som lagras i minnet. Dessutom kan beräkningen av uppskattningar startas först efter att resultaten av de första $k$-observationerna har ackumulerats. Det vill säga att dessa filter har en lång varaktighet av den transienta processen.

För att komma till rätta med denna brist är det nödvändigt att gå från ett filter med permanent minne till ett filter med växande minne. I ett sådant filter måste antalet observerade värden som ska utvärderas matcha numret n för den aktuella observationen. Detta gör det möjligt att få uppskattningar med utgångspunkt från antalet observationer lika med antalet komponenter i den uppskattade vektorn $X$. Och detta bestäms av ordningen på den antagna modellen, det vill säga hur många termer från Taylor-serien som används i modellen.

Samtidigt, när n ökar, förbättras filtrets utjämningsegenskaper, det vill säga att uppskattningarnas noggrannhet ökar. Den direkta implementeringen av detta tillvägagångssätt är dock förknippat med en ökning av beräkningskostnaderna. Därför implementeras växande minnesfilter som återkommande.

Poängen är att vi vid tidpunkten n redan har skattningen $X_((n-1)ots)$, som innehåller information om alla tidigare observationer $z_n, z_(n-1), z_(n-2) \dots z_ (n-(k-1))$. Uppskattningen $X_(not)$ erhålls av nästa observation $z_n$ med hjälp av informationen lagrad i uppskattningen $X_((n-1))(\mbox (ot))$. Denna procedur kallas återkommande filtrering och består av följande:

• enligt uppskattningen $X_((n-1))(\mbox (ots))$, förutsägs uppskattningen $X_n$ av formel 4 för $i = 1$: $X_(\mbox (noca priori)) = F_1X_((n-1 )ots)$. Detta är en uppskattning på förhand;
• enligt resultaten av den aktuella observationen $z_n$ omvandlas denna a priori uppskattning till en sann, det vill säga a posteriori;
• denna procedur upprepas vid varje steg, med start från $r+1$, där $r$ är filterordningen.

Den slutliga rekursiva filtreringsformeln ser ut så här:

$X_((n-1)ots) = X_(\mbox (nocapriori)) + (H^T_nH_n)^(-1)h^T_0(z_n - h_0 X_(\mbox (nocapriori)))$, (6 )

där för vårt andra ordningens filter:

Det växande minnesfiltret, som fungerar enligt formel 6, är ett specialfall av filtreringsalgoritmen som kallas Kalman-filtret.

I den praktiska implementeringen av denna formel måste man komma ihåg att a priori-uppskattningen som ingår i den bestäms av formel 4, och värdet $h_0 X_(\mbox (nocapriori))$ är den första komponenten i vektorn $X_( \mbox (nocapriori))$.

Det växande minnesfiltret har en viktig funktion. Om man tittar på Formel 6 är slutpoängen summan av den förväntade poängvektorn och korrigeringstermen. Denna korrigering är stor för små $n$ och minskar när $n$ ökar, och tenderar till noll som $n \rightarrow \infty$. Det vill säga när n växer växer filtrets utjämningsegenskaper och modellen som är inbäddad i det börjar dominera. Men den verkliga signalen kan motsvara modellen endast på separata avsnitt, så noggrannheten i prognosen försämras.

För att bekämpa detta, med start från några $n$, införs ett förbud mot ytterligare minskning av korrigeringstiden. Detta motsvarar att ändra filterbandet, det vill säga för litet n är filtret mer bredbandigt (mindre tröghet), för stort n blir det trögare.

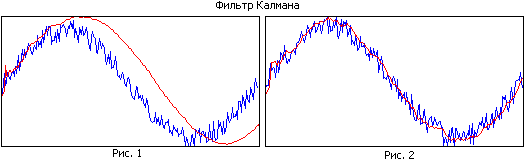
Jämför figur 1 och figur 2. I den första figuren har filtret ett stort minne, samtidigt som det jämnar ut bra, men på grund av det smala bandet ligger den uppskattade banan efter den verkliga. I den andra figuren är filterminnet mindre, det jämnar ut sämre, men det spårar den verkliga banan bättre.

Litteratur

1. Yu.M.Korshunov "Mathematical Foundations of Cybernetics"
2. A.V.Balakrishnan "Kalman filtration theory"
3. V.N. Fomin "Återkommande uppskattning och adaptiv filtrering"
4. C.F.N. Cowen, P.M. Bevilja "Adaptiva filter"

Figur 1

Således ligger paret vi letar efter någonstans på denna raka linje. Jag upprepar, det är omöjligt att från alla dessa alternativ välja det par som faktiskt fanns – vilket gav siffran 12, utan att ha några ytterligare ledtrådar. I alla fall, i den situation som Kalman-filtret uppfanns för finns det sådana tips. Det är något känt i förväg om slumptal. I synnerhet är det så kallade distributionshistogrammet för varje par av nummer känt där. Det erhålls vanligtvis efter tillräckligt långa observationer av nedfallet av dessa mycket slumpmässiga siffror. Det vill säga att det till exempel är känt av erfarenhet att i 5 % av fallen faller oftast paret x=1, y=8 ut (vi betecknar detta par enligt följande: (1,8)), i 2 % av fallen par x=2, y=3 ( 2,3), i 1 % av fallen ett par (3,1), i 0,024 % av fallen ett par (11,1), etc. Återigen är detta histogram satt för alla par siffror, inklusive de som summerar till 12. Således, för varje par som summerar till 12, kan vi säga att till exempel paret (1, 11) faller ut i 0,8 % av fallen, paret ( 2, 10) - i 1% av fallen, par (3, 9) - i 1,5% av fallen, etc. Således kan vi avgöra från histogrammet i vilken procent av fallen summan av termerna i ett par är 12. Låt till exempel summan i 30 % av fallen ge 12. Och i de återstående 70 % faller de återstående paren ut - dessa är (1.8), (2, 3), (3,1), etc. - de som summerar till andra tal än 12. Låt dessutom till exempel ett par (7,5) falla ut i 27% av fallen, medan alla andra par som ger totalt 12 faller ut i 0,024% + 0,8% + 1%+1,5%+…=3% av fallen. Så enligt histogrammet fick vi reda på att siffror som ger totalt 12 faller ut i 30 % av fallen. Samtidigt vet vi att om 12 ramlade ut så är orsaken oftast (27% av 30%) ett par (7,5). Det vill säga om redan 12 kastade, kan vi säga att i 90% (27% av 30% - eller, vad är detsamma, 27 gånger av varje 30) är anledningen till kast med 12 ett par (7,5). Att veta att paret (7,5) oftast är orsaken till att summan blir lika med 12, är det logiskt att anta att det med största sannolikhet föll ut nu. Naturligtvis är det fortfarande inte ett faktum att talet 12 faktiskt bildas av just detta par, men nästa gång, om vi stöter på 12, och vi återigen antar ett par (7,5), så är vi någonstans i 90% av fallen 100% rätt. Men om vi antar ett par (2, 10), kommer vi att ha rätt endast 1 % av 30 % av gångerna, vilket är lika med 3,33 % av korrekta gissningar jämfört med 90 % när vi gissar ett par (7,5). Det är allt - det här är poängen med Kalman-filteralgoritmen. Det vill säga, Kalman-filtret garanterar inte att det inte kommer att göra ett misstag vid bestämning av termen med summan, men det garanterar att det kommer att göra ett misstag det minsta antalet gånger (sannolikheten för ett fel kommer att vara minimal), eftersom den använder statistik - ett histogram för att falla ut ur par av siffror. Det bör också betonas att den så kallade sannolikhetsfördelningstätheten (PDD) ofta används i Kalman-filtreringsalgoritmen. Det måste dock förstås att innebörden där är densamma som histogrammets. Dessutom är ett histogram en funktion som bygger på PDF och är dess approximation (se till exempel ).
I princip kan vi avbilda detta histogram som en funktion av två variabler – det vill säga som en slags yta ovanför xy-planet. Där ytan är högre är sannolikheten för att motsvarande par faller ut också högre. Figur 2 visar en sådan yta.

fig.2

Som du kan se, ovanför linjen x + y = 12 (som är varianter av par som ger totalt 12), finns ytpunkter på olika höjder och den högsta höjden finns i varianten med koordinater (7,5). Och när vi stöter på en summa som är lika med 12, är i 90% av fallen paret (7,5) orsaken till att denna summa visas. De där. det är detta par, som summerar till 12, som har störst sannolikhet att inträffa, förutsatt att summan är 12.
Därför beskrivs idén bakom Kalman-filtret här. Det är på den som alla typer av dess modifieringar byggs - enstegs, flerstegs återkommande, etc. För en djupare studie av Kalmanfiltret rekommenderar jag boken: Van Tries G. Theory of detection, estimation and modulering.

p.s. För den som är intresserad av att förklara matematikens begrepp, det som kallas "på fingrarna", kan vi rekommendera den här boken och i synnerhet kapitlen från dess "Matematik"-sektion (du kan köpa själva boken eller enskilda kapitel från Det).

En studie gjordes av användningen av Kalman-filtret i moderna utvecklingar av komplex navigationssystem. Ett exempel på konstruktion ges och analyseras matematisk modell, som använder ett utökat Kalman-filter för att förbättra noggrannheten vid bestämning av koordinaterna för obemannade flygfarkoster. Delfiltret beaktas. Gjord kort recension vetenskapliga arbeten använder detta filter för att förbättra tillförlitligheten och feltoleransen hos navigationssystem. Denna artikel låter oss dra slutsatsen att användningen av Kalman-filtret i UAV-positioneringssystem praktiseras i många moderna utvecklingar. Det finns ett stort antal variationer och aspekter av denna användning, som också ger påtagliga resultat för att förbättra noggrannheten, särskilt i händelse av fel på standardsystem för satellitnavigering. Detta är huvudfaktorn i påverkan av denna teknik på olika vetenskapliga områden relaterade till utvecklingen av noggranna och feltoleranta navigationssystem för olika flygplan.

Kalman filter

navigering

obemannat flygfordon (UAV)

1. Makarenko G.K., Aleshechkin A.M. Undersökning av filtreringsalgoritmen för att bestämma koordinaterna för ett objekt från signalerna från satellitnavigeringssystem Doklady TUSUR. - 2012. - Nr 2 (26). - S. 15-18.

2. Bar-Shalom Y., Li X. R., Kirubarajan T. Uppskattning med applikationer

till spårning och navigering // Teorialgoritmer och programvara. - 2001. - Vol. 3. - S. 10-20.

3. Bassem I.S. Vision based Navigation (VBN) of Unmanned Aerial Vehicles (UAV) // UNIVERSITY OF CALGARY. - 2012. - Vol. 1. - S. 100-127.

4. Conte G., Doherty P. Ett integrerat UAV-navigeringssystem baserat på Aerial Image Matching // Aerospace Conference. - 2008. -Vol. 1. - P. 3142-3151.

5. Guoqiang M., Drake S., Anderson B. Design av ett utökat kalman-filter för UAV-lokalisering // In Information, Decision and Control. - 2007. - Vol. 7. – S. 224–229.

6. Ponda S.S banoptimering för mållokalisering med hjälp av små obemannade flygfarkoster // Massachusetts Institute of Technology. - 2008. - Vol. 1. - S. 64-70.

7. Wang J., Garrat M., Lambert A. Integration av gps/ins/vision-sensorer för att navigera obemannade flygfarkoster // IAPRS&SIS. - 2008. - Vol. 37. – s. 963-969.

En av de brådskande uppgifterna för modern navigering av obemannade flygfarkoster (UAV) är uppgiften att öka noggrannheten vid bestämning av koordinater. Detta problem löses genom att använda olika alternativ för att integrera navigationssystem. Ett av de moderna integrationsalternativen är kombinationen av gps/glonass-navigering med ett utökat Kalmanfilter, som rekursivt uppskattar noggrannheten med hjälp av ofullständiga och bullriga mätningar. För närvarande finns och utvecklas olika varianter av det utökade Kalman-filtret, inklusive ett varierat antal tillståndsvariabler. I detta arbete kommer vi att visa hur effektiv användningen kan vara i modern utveckling. Låt oss överväga en av de karakteristiska representationerna av ett sådant filter.

Att bygga en matematisk modell

PÅ detta exempel vi kommer bara att prata om UAV:s rörelse i horisontalplanet, annars kommer vi att överväga det så kallade 2d-lokaliseringsproblemet. I vårt fall motiveras detta av det faktum att UAV:en för många praktiskt förekommande situationer kan förbli ungefär på samma höjd. Detta antagande används ofta för att förenkla modellering av flygplansdynamik. Den dynamiska modellen för UAV ges av följande ekvationssystem:

där () - UAV-koordinater i horisontalplanet som en funktion av tid, UAV-riktning, UAV-vinkelhastighet och v UAV-markhastighet, fungerar och kommer att anses vara konstant. De är ömsesidigt oberoende, med kända kovarianser och , lika med respektive , och används för att simulera UAV-accelerationsförändringar orsakade av vind, pilotmanövrar, etc. Värdena och härleds från den maximala vinkelhastigheten för UAV och experimentvärdena för ändringarna i UAV:s linjära hastighet, - Kronecker-symbolen.

Detta ekvationssystem kommer att vara ungefärligt på grund av olinjäriteten i modellen och på grund av förekomsten av brus. Den enklaste approximationen i detta fall är Euler approximationen. Den diskreta modellen av det dynamiska rörelsesystemet UAV visas nedan.

diskret tillståndsvektor för Kalman-filtret, som tillåter approximering av värdet av en kontinuerlig tillståndsvektor. ∆ - tidsintervall mellan k och k+1 mätningar. () och () - sekvenser av vita Gaussiska brusvärden med noll medelvärde. Kovariansmatris för den första sekvensen:

På samma sätt, för den andra sekvensen:

Efter att ha gjort lämpliga substitutioner i ekvationerna i system (2) får vi:

Sekvenserna och är ömsesidigt oberoende. De är också noll-medelvärde vita Gaussiska brussekvenser med kovariansmatriser resp. Fördelen med denna form är att den visar förändringen i diskret brus mellan varje mätning. Som ett resultat får vi följande diskreta dynamiska modell:

(3)

Ekvation för:

= + , (4)

där x och y är koordinaterna för UAV vid k-tidpunkten, och är en Gaussisk sekvens av slumpmässiga parametrar med ett nollmedelvärde, som används för att ställa in felet. Denna sekvens antas vara oberoende av () och ().

Uttryck (3) och (4) tjänar som grund för att uppskatta platsen för UAV:en, var k-te koordinater erhålls med det utökade Kalman-filtret. Modellering av navigationssystems fel i förhållande till den här typen filter visar sin betydande effektivitet.

För större tydlighet ger vi ett litet enkelt exempel. Låt en del UAV flyga jämnt, med viss konstant acceleration a.

Där x är koordinaten för UAV vid t-tiden och δ är någon slumpvariabel.

Anta att vi har en gps-sensor som tar emot data om var ett flygplan befinner sig. Låt oss presentera resultatet av att modellera denna process i mjukvarupaketet MATLAB.

Ris. 1. Filtrering av sensoravläsningen med Kalman-filtret

På fig. 1 visar hur effektiv användningen av Kalman-filtrering kan vara.

Men i en verklig situation har signaler ofta icke-linjär dynamik och onormalt brus. Det är i sådana fall som det utökade Kalmanfiltret används. I händelse av att brusspridningarna inte är för stora (dvs en linjär approximation är tillräcklig), ger tillämpningen av det utökade Kalman-filtret en lösning på problemet med hög noggrannhet. Men när bruset inte är Gaussiskt kan det utökade Kalman-filtret inte användas. I det här fallet används vanligtvis ett partiellt filter, som använder numeriska metoder för att ta integraler baserade på Monte Carlo-metoder med Markov-kedjor.

Partikelfilter

Låt oss föreställa oss en av algoritmerna som utvecklar idéerna med det utökade Kalman-filtret - ett delfilter. Partiell filtrering är en suboptimal filtreringsmetod som fungerar när man utför Monte Carlo-kombination på en uppsättning partiklar som representerar sannolikhetsfördelningen för processen. Här är en partikel ett element taget från den tidigare fördelningen av den uppskattade parametern. Huvudidén med ett partiellt filter är att ett stort antal partiklar kan användas för att representera en distributionsuppskattning. Ju större antal partiklar som används, desto mer exakt kommer uppsättningen av partiklar att representera den tidigare fördelningen. Partikelfiltret initieras genom att sätta N partiklar i det från den tidigare fördelningen av parametrarna vi vill uppskatta. Filtreringsalgoritmen förutsätter att dessa partiklar passerar igenom specialsystem, och sedan viktning med hjälp av information erhållen från mätning av dessa partiklar. De resulterande partiklarna och deras associerade massor representerar den bakre fördelningen av utvärderingsprocessen. Cykeln upprepas för varje ny mätning och partikelvikterna uppdateras för att representera den efterföljande fördelningen. Ett av huvudproblemen med den traditionella partikelfiltreringsmetoden är att resultatet vanligtvis är ett fåtal partiklar som är mycket tunga, i motsats till de flesta andra som är mycket lätta. Detta leder till filtreringsinstabilitet. Detta problem kan lösas genom att införa en samplingshastighet, där N nya partiklar tas från en fördelning som består av gamla partiklar. Utvärderingsresultatet erhålls genom att erhålla ett prov av medelvärdet för flertalet partiklar. Om vi ​​har flera oberoende urval, kommer urvalets medelvärde att vara en exakt uppskattning av medelvärdet, som definierar den slutliga variansen.

Även om partikelfiltret inte är optimalt, när antalet partiklar tenderar till oändlighet, närmar sig effektiviteten hos algoritmen den Bayesianska uppskattningsregeln. Därför är det önskvärt att ha så många partiklar som möjligt för att erhålla bästa resultat. Tyvärr leder detta till en kraftig ökning av komplexiteten i beräkningar och tvingar följaktligen fram ett sökande efter en kompromiss mellan noggrannhet och beräkningshastighet. Så antalet partiklar bör väljas baserat på kraven för noggrannhetsbedömningsproblemet. En annan viktig faktor för driften av ett partikelfilter är begränsningen av provtagningshastigheten. Som tidigare nämnts är samplingshastigheten en viktig partikelfiltreringsparameter och utan den kommer algoritmen så småningom att bli degenererad. Tanken är att om vikterna är för ojämnt fördelade och provtagningströskeln snart nås, så kasseras partiklarna med låg vikt, och den återstående uppsättningen bildar en ny sannolikhetstäthet för vilken nya prover kan tas. Valet av samplingsfrekvenströskeln är en ganska svår uppgift, eftersom också hög frekvens gör att filtret blir för känsligt för brus, och för lågt ger ett stort fel. En annan viktig faktor är sannolikhetstätheten.

Generellt sett visar partikelfiltreringsalgoritmen bra positioneringsprestanda för stationära mål och för relativt långsamt rörliga mål med okänd accelerationsdynamik. Generellt sett är partikelfiltreringsalgoritmen mer stabil än det utökade Kalman-filtret och mindre benägen för degeneration och allvarliga fel. I fall av icke-linjär, icke-gaussisk fördelning denna algoritm filtrering visar en mycket god målplatsnoggrannhet, medan den utökade Kalman-filtreringsalgoritmen inte kan användas under sådana förhållanden. Nackdelarna med detta tillvägagångssätt inkluderar dess högre komplexitet i förhållande till det utökade Kalman-filtret, såväl som det faktum att det inte alltid är självklart hur man väljer rätt parametrar för denna algoritm.

Lovande forskning inom detta område

Användningen av en Kalman-filtermodell, som den vi har angett, kan ses i , där den används för att förbättra prestandan hos ett integrerat system (GPS + datorseende modell för matchning med en geografisk bas), och situationen för fel på satellitnavigeringsutrustning simuleras också. Med hjälp av Kalman-filtret förbättrades resultaten av systemdriften vid fel avsevärt (till exempel minskades felet vid bestämning av höjden med cirka två gånger, och felen vid bestämning av koordinaterna längs olika axlar reducerades nästan 9 gånger). En liknande användning av Kalman-filtret ges också i .

Ett intressant problem ur en uppsättning metoders synvinkel löses i . Den använder också ett 5-läges Kalman-filter, med vissa skillnader i modellbyggandet. Det erhållna resultatet överstiger resultatet av vår modell på grund av användningen av ytterligare metoder för integration (foto och termiska bilder används). Tillämpningen av Kalman-filtret i detta fall gör det möjligt att reducera felet vid bestämning av de rumsliga koordinaterna för en given punkt till ett värde av 5,5 m.

Slutsats

Sammanfattningsvis noterar vi att användningen av Kalman-filtret i UAV-positioneringssystem praktiseras i många moderna utvecklingar. Det finns ett stort antal variationer och aspekter av denna användning, upp till samtidig användning av flera liknande filter med olika tillståndsfaktorer. Ett av de mest lovande områdena för utvecklingen av Kalman-filter är arbetet med att skapa ett modifierat filter, vars fel kommer att representeras av färgbrus, vilket kommer att göra det ännu mer värdefullt för att lösa verkliga problem. Av stort intresse inom tekniken är också ett partiellt filter med vilket icke-Gaussiskt brus kan filtreras. Denna mångfald och påtagliga resultat för att förbättra noggrannheten, särskilt i händelse av fel påm, är de viktigaste faktorerna som påverkar denna teknik inom olika vetenskapliga områden relaterade till utvecklingen av noggranna och feltoleranta navigationssystem för olika flygplan.

Recensenter:

Labunets V.G., doktor i tekniska vetenskaper, professor, professor vid institutionen teoretiska grunder Radio Engineering Ural Federal University uppkallad efter Rysslands första president B.N. Jeltsin, Jekaterinburg;

Ivanov V.E., doktor i tekniska vetenskaper, professor, chef. Institutionen för teknik och kommunikation, Ural Federal University uppkallad efter Rysslands första president B.N. Jeltsin, Jekaterinburg.

Bibliografisk länk

Random Forest är en av mina favoritalgoritmer för datautvinning. För det första är den otroligt mångsidig, den kan användas för att lösa både regressions- och klassificeringsproblem. Sök efter anomalier och välj prediktorer. För det andra är detta en algoritm som är riktigt svår att tillämpa felaktigt. Helt enkelt för att den, till skillnad från andra algoritmer, har få anpassningsbara parametrar. Och ändå är det förvånansvärt enkelt i sin essens. Samtidigt är det anmärkningsvärt korrekt.

Vad är tanken med en sådan underbar algoritm? Tanken är enkel: låt oss säga att vi har en väldigt svag algoritm, säg . Om vi ​​gör många olika modeller med denna svaga algoritm och genomsnitt resultatet av deras förutsägelser, så kommer slutresultatet att bli mycket bättre. Detta är den så kallade ensemble learning in action. Random Forest-algoritmen kallas därför "Random Forest", för den mottagna data skapar den många beslutsträd och beräknar sedan ett genomsnitt av resultatet av deras förutsägelser. En viktig punkt här är elementet av slumpmässighet i skapandet av varje träd. När allt kommer omkring är det tydligt att om vi skapar många identiska träd, kommer resultatet av deras medelvärde att ha samma noggrannhet som ett träd.

Hur fungerar han? Anta att vi har lite indata. Varje kolumn motsvarar någon parameter, varje rad motsvarar något dataelement.

Vi kan slumpmässigt välja ett antal kolumner och rader från hela datasetet och bygga ett beslutsträd från dem.

Torsdagen den 10 maj 2012

Torsdagen den 12 januari 2012

Allt började i april 2011 när jag hade en telefonintervju med Zynga. Sedan verkade det hela som något slags spel som inte hade något med verkligheten att göra, och jag kunde inte ens föreställa mig vad det skulle leda till. I juni 2011 kom Zynga till Moskva och genomförde en serie intervjuer, cirka 60 kandidater som klarade en telefonintervju övervägdes och cirka 15 personer valdes ut från dem (jag vet inte det exakta antalet, någon ändrade sig senare, någon vägrade omedelbart). Intervjun visade sig vara förvånansvärt enkel. Inga programmeringsuppgifter för dig, inga intrikata frågor om formen på luckor, främst möjligheten att chatta testades. Och kunskap, enligt min mening, utvärderades endast ytligt.

Och så började bråket. Först väntade vi på resultatet, sedan erbjudandet, sedan godkännandet av LCA, sedan godkännandet av ansökan om visum, sedan dokumenten från USA, sedan linjen vid ambassaden, sedan den extra kontrollen, sedan visumet. Ibland verkade det för mig att jag var redo att släppa allt och göra mål. Ibland tvivlade jag på om vi behöver detta Amerika, för Ryssland är inte heller dåligt. Hela processen tog ungefär ett halvår, till slut, i mitten av december, fick vi visum och började förbereda oss för avresa.

Måndagen var min första dag på det nya jobbet. Kontoret har alla förutsättningar att inte bara arbeta, utan också att leva. Frukostar, luncher och middagar från våra egna kockar, ett gäng varierad mat fylld i alla hörn, gym, massage och även frisör. Allt detta är helt gratis för anställda. Många tar sig till jobbet med cykel och flera rum är utrustade för att förvara fordon. I allmänhet har jag aldrig sett något liknande i Ryssland. Allt har dock sitt pris, vi blev direkt förvarnade om att vi skulle behöva jobba mycket. Vad som är "mycket", enligt deras mått mätt, är inte särskilt tydligt för mig.

Jag hoppas dock att jag, trots mängden arbete, inom överskådlig framtid kommer att kunna återuppta bloggandet och kanske berätta något om det amerikanska livet och att jobba som programmerare i Amerika. Vänta och se. Under tiden önskar jag er alla en god jul och ett gott nytt år så ses vi snart!

resultat<- NULL for(i in (1:length(divs[,1]))){ d <- divs if (d$Divs>0)( försök(( citat<- getSymbols(d$Symbol, src="Finam", from="2010-01-01", auto.assign=FALSE) if (!is.nan(quotes)){ price <- Cl(quotes) if (length(price)>0)(dd<- d$Divs result <- rbind(result, data.frame(d$Symbol, d$Name, d$RegistryDate, as.numeric(dd)/as.numeric(price), stringsAsFactors=FALSE)) } } }, silent=TRUE) } } colnames(result) <- c("Symbol", "Name", "RegistryDate", "Divs") result

På Internet, bland annat på Habré, kan du hitta mycket information om Kalmanfiltret. Men det är svårt att hitta en lättsmält härledning av själva formlerna. Utan en slutsats uppfattas all denna vetenskap som en sorts shamanism, formlerna ser ut som en ansiktslös uppsättning symboler, och viktigast av allt är att många enkla påståenden som ligger på teorins yta är bortom förståelse. Syftet med den här artikeln är att prata om detta filter på det mest tillgängliga språket.
Kalman-filtret är ett kraftfullt datafiltreringsverktyg. Dess huvudprincip är att vid filtrering används information om själva fenomenets fysik. Säg, om du filtrerar data från en bils hastighetsmätare, så ger bilens tröghet dig rätten att uppfatta för snabba hastighetshopp som ett mätfel. Kalman-filtret är intressant eftersom det på sätt och vis är det bästa filtret. Vi kommer att diskutera mer i detalj nedan vad exakt orden "det bästa" betyder. I slutet av artikeln ska jag visa att formlerna i många fall kan förenklas så till den grad att nästan ingenting blir kvar av dem.

Likbez

Innan jag bekantar mig med Kalman-filtret, föreslår jag att erinra om några enkla definitioner och fakta från sannolikhetsteorin.

Slumpmässigt värde

När de säger att ett slumpmässigt värde ges, menar de att detta värde kan anta slumpmässiga värden. Det antar olika värden med olika sannolikheter. När du kastar, säg, en tärning, kommer en diskret uppsättning värden att falla ut: . När det till exempel gäller hastigheten på en vandrande partikel, så måste man uppenbarligen hantera en kontinuerlig uppsättning värden. "Tappade" värden för en slumpvariabel kommer att betecknas med , men ibland kommer vi att använda samma bokstav som betecknar en slumpvariabel: .
I fallet med en kontinuerlig uppsättning värden kännetecknas den slumpmässiga variabeln av sannolikhetstätheten , vilket dikterar för oss att sannolikheten för att den slumpmässiga variabeln "faller ut" i ett litet område av en längdpunkt är lika med . Som vi kan se från bilden är denna sannolikhet lika med arean av den skuggade rektangeln under grafen:

Ganska ofta i livet fördelas slumpvariabler enligt Gauss, när sannolikhetstätheten är .

Vi ser att funktionen har formen av en klocka centrerad i en punkt och med en karakteristisk bredd i storleksordningen .
Eftersom vi pratar om den gaussiska fördelningen skulle det vara synd att inte tala om var den kom ifrån. Precis som siffror är fast etablerade i matematik och dyker upp på de mest oväntade platser, så har den Gaussiska fördelningen slagit djupa rötter i sannolikhetsteorin. Ett anmärkningsvärt uttalande som delvis förklarar den Gaussiska allestädes närvarande är följande:
Låt det finnas en slumpvariabel som har en godtycklig fördelning (det finns faktiskt vissa begränsningar för denna godtycke, men de är inte alls stela). Låt oss utföra experiment och beräkna summan av de "bortfallna" värdena för en slumpvariabel. Låt oss göra många av dessa experiment. Det är klart att vi varje gång kommer att få ett annat värde på summan. Denna summa är med andra ord i sig en stokastisk variabel med sin egen bestämda fördelningslag. Det visar sig att för tillräckligt stor, fördelningen av denna summa tenderar till den gaussiska fördelningen (förresten, den karakteristiska bredden på "klockan" växer med ). Läs mer på wikipedia: central limit theorem. I livet finns det mycket ofta kvantiteter som består av ett stort antal lika fördelade oberoende slumpvariabler, och därför är fördelade enligt Gauss.

Betyda

Medelvärdet för en slumpvariabel är vad vi får i gränsen om vi gör många experiment och beräknar det aritmetiska medelvärdet av de tappade värdena. Medelvärdet anges på olika sätt: matematiker betecknar gärna med (förväntning), och utländska matematiker med (förväntning). Fysik samma genom eller. Vi kommer att utse på ett främmande sätt:.
Till exempel, för en Gauss-fördelning är medelvärdet .

Dispersion

När det gäller den Gaussiska fördelningen kan vi tydligt se att den slumpmässiga variabeln föredrar att falla ut i någon närhet av sitt medelvärde . Som framgår av grafen är den karakteristiska spridningen av ordningsvärden . Hur kan vi uppskatta denna spridning av värden för en godtycklig slumpvariabel om vi vet dess fördelning. Du kan rita en graf över dess sannolikhetstäthet och uppskatta den karakteristiska bredden med ögat. Men vi föredrar att gå den algebraiska vägen. Du kan hitta medellängden för avvikelsen (modulen) från medelvärdet: . Detta värde kommer att vara en bra uppskattning av den karakteristiska spridningen av värden. Men du och jag vet mycket väl att det är en huvudvärk att använda moduler i formler, så denna formel används sällan för att uppskatta den karakteristiska spridningen.
Ett enklare sätt (enkelt i termer av beräkningar) är att hitta . Denna kvantitet kallas varians och kallas ofta . Roten till variansen kallas standardavvikelsen. Standardavvikelsen är en bra uppskattning av spridningen av en slumpvariabel.
För en Gaussfördelning kan vi till exempel anta att variansen som definieras ovan är exakt lika med , vilket betyder att standardavvikelsen är lika med , vilket stämmer mycket väl överens med vår geometriska intuition.
Det finns faktiskt en liten bluff gömd här. Faktum är att i definitionen av den Gaussiska fördelningen, under exponenten är uttrycket . Dessa två i nämnaren är just så att standardavvikelsen skulle vara lika med koefficienten. Det vill säga att den Gaussiska fördelningsformeln i sig är skriven i en form som är speciellt skärpt för det faktum att vi kommer att överväga dess standardavvikelse.

Oberoende slumpvariabler

Slumpvariabler kan vara beroende eller inte. Föreställ dig att du kastar en nål på ett plan och skriver ner koordinaterna för båda ändarna av det. Dessa två koordinater är beroende, de är förbundna med villkoret att avståndet mellan dem alltid är lika med nålens längd, även om de är slumpvariabler.
Slumpvariabler är oberoende om utfallet av den första är helt oberoende av utfallet av den andra. Om de slumpmässiga variablerna och är oberoende, är medelvärdet av deras produkt lika med produkten av deras medelvärden:

Bevis

Att till exempel ha blå ögon och avsluta skolan med en guldmedalj är oberoende slumpvariabler. Om blåögda, säg en guldmedaljörer, då blåögda medaljörer Detta exempel säger oss att om slumpvariabler och ges av deras sannolikhetstätheter och , så uttrycks oberoendet av dessa storheter i det faktum att sannolikhetstätheten (den första värde tappade , och det andra ) hittas av formeln:

Av detta följer omedelbart att:

Som du kan se utförs beviset för slumpvariabler som har ett kontinuerligt spektrum av värden och ges av deras sannolikhetstäthet. I andra fall är idén med beviset liknande.

Kalman filter

Formulering av problemet

Beteckna med värdet som vi ska mäta och sedan filtrera. Det kan vara koordinat, hastighet, acceleration, luftfuktighet, stinkgrad, temperatur, tryck osv.
Låt oss börja med ett enkelt exempel, som kommer att leda oss till formuleringen av ett allmänt problem. Föreställ dig att vi har en radiostyrd bil som bara kan åka framåt och bakåt. Vi, med kännedom om bilens vikt, form, vägbana etc., beräknade hur den styrande joysticken påverkar rörelsehastigheten.

Då kommer maskinens koordinater att ändras enligt lagen:

I verkligheten kan vi i våra beräkningar inte ta hänsyn till små störningar som verkar på bilen (vind, gupp, småsten på vägen), så bilens verkliga hastighet kommer att skilja sig från den beräknade. En slumpvariabel läggs till till höger om den skrivna ekvationen:

Vi har en GPS-sensor installerad på bilen, som försöker mäta bilens sanna koordinat, och som naturligtvis inte kan mäta den exakt, utan mäter den med ett fel, som också är en slumpmässig variabel. Som ett resultat får vi felaktiga data från sensorn:

Problemet är att, med de felaktiga sensoravläsningarna, hitta en bra approximation för maskinens sanna koordinat.
I formuleringen av det allmänna problemet kan vad som helst vara ansvarigt för koordinaten (temperatur, luftfuktighet ...), och vi kommer att beteckna termen som ansvarar för att styra systemet utifrån som (i exemplet med maskinen). Ekvationerna för koordinat- och sensoravläsningarna kommer att se ut så här:

Låt oss diskutera i detalj vad vi vet:

Det är användbart att notera att filtreringsuppgiften inte är en utjämningsuppgift. Vi siktar inte på att jämna ut data från sensorn, vi siktar på att få det närmaste värdet till den verkliga koordinaten.

Kalman algoritm

Vi resonerar genom induktion. Föreställ dig att vi i det -e steget redan har hittat det filtrerade värdet från sensorn, som väl approximerar den sanna koordinaten för systemet. Glöm inte att vi känner till ekvationen som styr förändringen av en okänd koordinat:

Därför, utan att få värdet från sensorn ännu, kan vi anta att i steget utvecklas systemet enligt denna lag och sensorn kommer att visa något nära . Tyvärr kan vi inte säga något mer exakt än. Å andra sidan, vid steget kommer vi att ha en felaktig sensoravläsning på våra händer.
Kalmans idé är följande. För att få den bästa approximationen till den sanna koordinaten måste vi välja en mellanväg mellan den felaktiga sensoravläsningen och vår förutsägelse av vad vi förväntade oss att den skulle se. Vi kommer att ge sensoravläsningen en vikt och det förutsagda värdet kommer att ha en vikt:

Koefficienten kallas för Kalmankoefficienten. Det beror på iterationssteget, så det skulle vara mer korrekt att skriva , men för nu, för att inte röra ihop beräkningsformlerna, kommer vi att utelämna dess index.
Vi måste välja Kalman-koefficienten på ett sådant sätt att det resulterande optimala värdet på koordinaten skulle vara närmast det sanna värdet. Till exempel, om vi vet att vår sensor är mycket exakt, kommer vi att lita mer på dess avläsning och ge värdet mer vikt (nära ett). Om sensorn, tvärtom, inte alls är korrekt, kommer vi att fokusera mer på det teoretiskt förutsagda värdet på .
I allmänhet, för att hitta det exakta värdet på Kalman-koefficienten, behöver man helt enkelt minimera felet:

Vi använder ekvationerna (1) (de i den blå rutan) för att skriva om uttrycket för felet:

Bevis

Nu är det dags att diskutera vad uttrycket minimera fel betyder? Trots allt är felet, som vi ser, i sig en slumpvariabel och får varje gång olika värden. Det finns verkligen inte en enstaka metod för att definiera vad det innebär att felet är minimalt. Precis som i fallet med variansen för en slumpvariabel, när vi försökte uppskatta den karakteristiska bredden på dess spridning, kommer vi här att välja det enklaste kriteriet för beräkningar. Vi kommer att minimera medelvärdet från det kvadratiska felet:

Låt oss skriva det sista uttrycket:

Bevis

Av det faktum att alla slumpvariabler som ingår i uttrycket för är oberoende, följer att alla "kors"-termer är lika med noll:

Vi använde det faktum att , då ser formeln för variansen mycket enklare ut: .

Detta uttryck får ett minimivärde när (likställer derivatan med noll):

Här skriver vi redan ett uttryck för Kalman-koefficienten med stegindex, därför betonar vi att det beror på iterationssteget.
Vi ersätter det erhållna optimala värdet med uttrycket som vi har minimerat. Vi tar emot;

Vår uppgift är löst. Vi har fått en iterativ formel för att beräkna Kalman-koefficienten.
Låt oss sammanfatta vår förvärvade kunskap i en ram:

Exempel

Matlab kod

Rensa alla; N=100% antal prover a=0,1% acceleration sigmaPsi=1 sigmaEta=50; k=l:Nx=kx(1)=0 z(1)=x(1)+normrnd(0,sigmaEta); för t=1:(N-1) x(t+l)=x(t)+a*t+normrnd(0,sigmaPsi); z(t+l)=x(t+l)+normrnd(0,sigmaEta); slutet; %kalman filter xOpt(1)=z(1); eOpt(1)=sigmaEta; för t=1:(N-1) eOpt(t+1)=sqrt((sigmaEta^2)*(eOpt(t)^2+sigmaPsi^2)/(sigmaEta^2+eOpt(t)^2+ sigmaPsi^2)) K(t+1)=(eOpt(t+1))^2/sigmaEta^2 xOpt(t+1)=(xOpt(t)+a*t)*(1-K(t) +1))+K(t+l)*z(t+1) slut; plot(k,xopt,k,z,k,x)

Analys

Om vi ​​spårar hur Kalman-koefficienten förändras med iterationssteget, så kan vi visa att den alltid stabiliseras till ett visst värde. Till exempel, när RMS-felen för sensorn och modellen relaterar till varandra som tio till ett, ser grafen för Kalman-koefficienten beroende på iterationssteget ut så här:

I följande exempel kommer vi att diskutera hur detta kan göra våra liv mycket enklare.

Andra exemplet

I praktiken händer det ofta att vi inte vet något alls om den fysiska modellen av vad vi filtrerar. Du vill till exempel filtrera avläsningar från din favoritaccelerometer. Du vet inte i förväg enligt vilken lag du tänker vrida accelerometern. Den mest information du kan få fram är sensorfelsvariationen. I en sådan svår situation kan all okunnighet om rörelsemodellen drivas in i en slumpvariabel:

Men ärligt talat uppfyller ett sådant system inte längre de villkor som vi ålade den slumpmässiga variabeln, för nu är all rörelsefysik som är okänd för oss gömd där, och därför kan vi inte säga att vid olika tidpunkter, felen i modell är oberoende av varandra och att deras medelvärden är noll. I det här fallet är teorin om Kalman-filtret i stort sett inte tillämplig. Men vi kommer inte att uppmärksamma detta faktum, utan dumt tillämpa all kolossen av formler, välja koefficienter och med ögat, så att de filtrerade uppgifterna ser vackra ut.
Men det finns en annan, mycket enklare väg att gå. Som vi såg ovan stabiliseras Kalman-koefficienten alltid till värdet . Därför, istället för att välja koefficienterna och och hitta Kalman-koefficienten med hjälp av komplexa formler, kan vi betrakta denna koefficient som alltid en konstant, och välja endast denna konstant. Detta antagande kommer att förstöra nästan ingenting. För det första använder vi redan olagligt Kalman-teorin, och för det andra stabiliseras Kalman-koefficienten snabbt till en konstant. I slutändan kommer allt att bli väldigt enkelt. Vi behöver inga formler från Kalmans teori alls, vi behöver bara välja ett acceptabelt värde och infoga det i den iterativa formeln:

Följande graf visar data från en fiktiv sensor filtrerad på två olika sätt. Förutsatt att vi inte vet något om fenomenets fysik. Det första sättet är ärligt, med alla formler från Kalmans teori. Och den andra är förenklad, utan formler.

Som vi kan se är metoderna nästan desamma. En liten skillnad observeras först i början, när Kalman-koefficienten ännu inte har stabiliserats.

Diskussion

Som vi har sett är huvudidén med Kalman-filtret att hitta en koefficient så att det filtrerade värdet

skulle i genomsnitt skilja sig minst av allt från koordinatens verkliga värde. Vi ser att det filtrerade värdet är en linjär funktion av sensoravläsningen och det tidigare filtrerade värdet. Och det tidigare filtrerade värdet är i sin tur en linjär funktion av sensoravläsningen och det tidigare filtrerade värdet . Och så vidare, tills kedjan är helt utfälld. Det vill säga det filtrerade värdet beror på Allt tidigare sensoravläsningar linjärt:

Därför kallas Kalman-filtret för ett linjärt filter.
Det kan bevisas att Kalman-filtret är det bästa av alla linjära filter. Det bästa i den meningen att medelkvadraten för filterfelet är minimal.

Multivariat fall

Hela Kalman-filterteorin kan generaliseras till det flerdimensionella fallet. Formlerna där ser lite läskigare ut, men själva idén om deras härledning är densamma som i det endimensionella fallet. Du kan se dem i denna utmärkta artikel: http://habrahabr.ru/post/140274/ .
Och i detta underbara video- ett exempel på hur man använder dem.