Kombinované použitie pid regulátora a kalmanovho filtra. Aplikácia Kalmanovho filtra na spracovanie sekvencie súradníc GPS. Kovariančná matica šumu merania

Random Forest je jeden z mojich obľúbených algoritmov na dolovanie údajov. Po prvé, je neuveriteľne všestranný, dá sa použiť na riešenie regresných aj klasifikačných problémov. Vyhľadajte anomálie a vyberte prediktory. Po druhé, toto je algoritmus, ktorý je naozaj ťažké nesprávne aplikovať. Jednoducho preto, že na rozdiel od iných algoritmov má málo prispôsobiteľných parametrov. A predsa je vo svojej podstate prekvapivo jednoduchý. Zároveň je pozoruhodne presný.

Aká je myšlienka takého úžasného algoritmu? Myšlienka je jednoduchá: povedzme, že máme nejaký veľmi slabý algoritmus, povedzme . Ak vytvoríme veľa rôznych modelov pomocou tohto slabého algoritmu a spriemerujeme výsledok ich predpovedí, potom bude konečný výsledok oveľa lepší. Ide o takzvané súborové učenie v akcii. Algoritmus náhodného lesa sa preto nazýva „náhodný les“, pre prijaté údaje vytvára mnoho rozhodovacích stromov a potom spriemeruje výsledok ich predpovedí. Dôležitým bodom je tu prvok náhodnosti pri vytváraní každého stromu. Je predsa jasné, že ak vytvoríme veľa rovnakých stromov, tak výsledok ich spriemerovania bude mať presnosť jedného stromu.

ako pracuje? Predpokladajme, že máme nejaké vstupné údaje. Každý stĺpec zodpovedá nejakému parametru, každý riadok zodpovedá nejakému dátovému prvku.

Môžeme si náhodne vybrať množstvo stĺpcov a riadkov z celého súboru údajov a zostaviť z nich rozhodovací strom.

štvrtok 10. mája 2012

štvrtok 12. januára 2012

Všetko to začalo v apríli 2011, keď som mal telefonický rozhovor so Zyngou. Potom mi to všetko pripadalo ako nejaká hra, ktorá nemá nič spoločné s realitou a ani som si nevedel predstaviť, k čomu to povedie. V júni 2011 Zynga pricestovala do Moskvy a urobila sériu pohovorov, zvažovalo sa asi 60 kandidátov, ktorí prešli telefonickým pohovorom a z nich sa vybralo asi 15 ľudí (neviem presný počet, niekto si to neskôr rozmyslel, niekto okamžite odmietol). Rozhovor sa ukázal byť prekvapivo jednoduchý. Žiadne programovacie úlohy pre vás, žiadne zložité otázky o tvare poklopov, testovala sa hlavne schopnosť chatovať. A vedomosti sa podľa mňa hodnotili len povrchne.

A potom začala hádka. Najprv sme čakali na výsledky, potom ponuku, potom schválenie LCA, potom schválenie žiadosti o vízum, potom dokumenty z USA, potom linku na veľvyslanectve, potom dodatočnú kontrolu, potom víza. Miestami sa mi zdalo, že som pripravený všetko zahodiť a skórovať. Občas som pochyboval, či túto Ameriku potrebujeme, pretože ani Rusko nie je zlé. Celý proces trval asi pol roka, nakoniec sme v polovici decembra dostali víza a začali sa pripravovať na odlet.

Pondelok bol môj prvý deň v novej práci. Kancelária má všetky podmienky nielen pracovať, ale aj bývať. Raňajky, obedy a večere od vlastných kuchárov, kopa pestrého jedla napchatého vo všetkých kútoch, posilňovňa, masáže a dokonca aj kaderníctvo. To všetko je pre zamestnancov úplne zadarmo. Mnohí sa dostávajú do práce na bicykli a niekoľko miestností je vybavených na uskladnenie vozidiel. Vo všeobecnosti som v Rusku nikdy nič také nevidel. Všetko má však svoju cenu, hneď nás upozornili, že budeme musieť veľa pracovať. Čo je podľa ich štandardov „veľa“, mi nie je veľmi jasné.

Dúfam však, že aj napriek množstvu práce sa mi v dohľadnej dobe podarí obnoviť blogovanie a možno porozprávať niečo o americkom živote a práci programátora v Amerike. Počkaj a uvidíš. Zatiaľ vám všetkým prajem veselé Vianoce a šťastný nový rok a do skorého videnia!

výsledok<- NULL for(i in (1:length(divs[,1]))){ d <- divs if (d$Divs>0)( skúste(( úvodzovky<- getSymbols(d$Symbol, src="Finam", from="2010-01-01", auto.assign=FALSE) if (!is.nan(quotes)){ price <- Cl(quotes) if (length(price)>0) (dd<- d$Divs result <- rbind(result, data.frame(d$Symbol, d$Name, d$RegistryDate, as.numeric(dd)/as.numeric(price), stringsAsFactors=FALSE)) } } }, silent=TRUE) } } colnames(result) <- c("Symbol", "Name", "RegistryDate", "Divs") result

prepis

1 # 09, september 2015 MDT Aplikácia Kalmanovho filtra na spracovanie sekvencie GPS súradníc Listerenko R.R., Bachelor Russia, Moskva, MSTU im. N.E. Bauman, oddelenie" softvér počítače a Informačné technológie» Školiteľ: Bekasov D.E., asistent Rusko, Moskva, MSTU im. N.E. Bauman, Katedra počítačového softvéru a informačných technológií Úloha filtrovania GPS súradníc V súčasnosti sú široko využívané služby GPS sledovania, ktorých úlohou je sledovať trasy pozorovaných objektov za účelom ich uloženia a ďalšej reprodukcie a analýzy. Avšak v dôsledku chyby snímača GPS z viacerých dôvodov, ako je strata signálu zo satelitu, zmena geometrie umiestnenia satelitov, odrazy signálu, chyby vo výpočte a chyby zaokrúhľovania, konečný výsledok nie je presne zodpovedať trase objektu. Existujú ako malé odchýlky (do 100 m), ktoré nebránia vnímaniu vizuálnych informácií o trase a jej analýze, tak veľmi významné (do 1 km, v prípade straty satelitného signálu a používania základňových staníc až na niekoľko desiatok km). Na demonštráciu výsledku algoritmu uvedeného v článku sa používa trasa obsahujúca odchýlky od skutočnej polohy presahujúce niekoľko kilometrov. Na opravu takýchto chýb je vyvinutý algoritmus, ktorý vykonáva transformáciu postupnosti súradníc. Vstupnými dátami pre algoritmus je sekvencia GPS súradníc. Každá súradnica obsahuje nasledujúce informácie prijaté zo senzora: Zemepisná šírka Dĺžka Azimut v stupňoch Okamžitá rýchlosť objektu v danom bode v m/s

2 Možná odchýlka súradníc objektu od skutočnej hodnoty v metroch Čas prijatia súradnice snímačom Výsledkom algoritmu je postupnosť súradníc s opravenou zemepisnou šírkou a dĺžkou. Ako základ pre zostavenie algoritmu sa rozhodlo použiť Kalmanov filter, pretože vám umožňuje samostatne brať do úvahy chyby merania a chyby náhodného procesu, ako aj použiť rýchlosť objektu prijatého zo snímača. Budovanie matematický model použitie Kalmanovho filtra Na použitie Kalmanovho filtra je potrebné, aby bol skúmaný proces opísaný nasledovne: = + + (1) = + (2) do stavu. Vektor popisuje riadiace akcie v procese. Matica B s rozmermi n l mapuje vektor riadiacich akcií u do zmeny stavu s. je náhodná premenná opisujúca chyby skúmaného procesu a ~0, kde Q je kovariančná matica chýb procesu. Vzorec (2) opisuje merania náhodného procesu. - vektor meraného stavu procesu, matica H s rozmermi m n mapuje stav procesu na meranie procesu. - náhodná premenná charakterizujúca chyby merania a ~0, kde P je kovariančná matica chýb merania. Keďže sa skúma proces pohybu objektu, stavová rovnica je zostavená na základe pohybovej rovnice telesa = + +!" #$ % & ". Okrem toho neexistujú žiadne ďalšie informácie o pohybovom procese, takže sa predpokladá, že riadiaci úkon je 0. Za stav procesu sa berie vektor = + () *, -. +, kde x, y - súradnice objektu, - projekcie rýchlosti objektu. Pre uvažovaný proces teda rovnica (1) nadobúda nasledujúci tvar: = + /!, (3)

3 kde = ! = 3! + 7 " 0 ; 6 2: 6 " / = : 6 0: 6 2: 6 0: , (4)!,4, (5) (6) V tomto modeli sa zrýchlenie objektu považuje za náhodné chyba procesu. Vychádzajú z nasledujúcich predpokladov: a) Zrýchlenia pozdĺž rôznych osí sú nezávislé náhodné premenné.),* b)

4 = AB = C. CE = C/!!. /. = /C!!. /. Keďže zložky vektora ak (5) sú nezávislé náhodné premenné, potom C!!. = " 0 " G. Vzorec (7) má teda nasledujúci tvar: = / " (8) Vektor merania zk pre tento problém je reprezentovaný takto: H I = 0 + J, J (7) 2, (9) kde H, I - súradnice objektu prijatého zo snímača, J +,J, - rýchlosť objektu prijatého zo snímača Matica H vo vzorci (2) sa rovná identifikačnej matici s rozmermi 4 4, keďže v rámci v rámci tejto úlohy sa uvažuje, že meranie je lineárny kombinovaný stavový vektor a niektoré náhodné chyby. Predpokladá sa, že je daná matica R chýb merania. možnosti jeho výpočet je použitie údajov o odhadovanej presnosti merania prijatého zo snímača. Aplikácia Kalmanovho filtra na skonštruovaný model Pre aplikáciu filtra je potrebné zaviesť nasledujúce pojmy: - posteriori odhad stavu objektu v čase k, získaný z výsledkov pozorovaní do času k vrátane. L je nekorigovaný a posteriori odhad stavu objektu v čase k. - aposteriorná chybová kovariančná matica, ktorá špecifikuje odhad presnosti získaného odhadu stavového vektora a zahŕňa odhad chybových rozptylov vypočítaného stavu a kovariancie, zobrazujúci zistené vzťahy medzi stavovými parametrami systému. L je neupravená kovariančná matica zadnej chyby. Matica P0 je nastavená na nulu, pretože sa predpokladá, že počiatočná poloha objektu je známa. Mládežnícky vedecko-technický bulletin Federálneho zhromaždenia, ISSN

5 Jedna iterácia Kalmanovho filtra pozostáva z dvoch krokov: extrapolácia a korekcia. a) V štádiu extrapolácie sa odhad L vypočíta z odhadu stavového vektora L a chybovej kovariančnej matice L podľa nasledujúcich vzorcov: L =, (10) L =. +, (11) kde maticu Ak poznáme zo vzorca (4), maticu Qk vypočítame zo vzorca (8). b) V štádiu korekcie sa matica zisku Kk vypočíta podľa nasledujúceho vzorca: M = L. L. + (12) kde sa predpokladá, že R, H sú známe. Kk sa používa na korekciu odhadu stavu objektu L a chybovej kovariančnej matice L takto: = L + M L, (13) = N M L, (14) kde I je matica identity. Je potrebné poznamenať, že na použitie vyššie uvedených pomerov je potrebné, aby jednotky merania pre parametre objektu zahrnuté vo výpočtoch boli konzistentné. V pôvodných údajoch sú však zemepisná šírka a dĺžka uvedené v uhlových súradniciach a rýchlosť v metrických jednotkách. Okrem toho je tiež pohodlnejšie špecifikovať zrýchlenie pre výpočet chyby procesu v metrických jednotkách. Na prevod rýchlosti a zrýchlenia na uhlové jednotky sa používajú Vincentiho vzorce. Výsledok filtra na obr. 1 znázorňuje príklad cesty pred spracovaním. Je vidieť, že v tento príklad existuje niekoľko súradníc s vysokou mierou chyby, ktorá je vyjadrená prítomnosťou "vrcholov" súradníc, ktoré sú výrazne odstránené z hlavnej trasy. Na obr. 2 je znázornený výsledok filtračnej operácie s touto cestou.

6 Obr. 1. Trasa objektu Obr. 2. Trasa objektu po aplikovaní filtra Výsledkom je, že prakticky neexistujú žiadne „vrcholy“, okrem najväčšieho, ktorý bol citeľne zmenšený a zvyšok trasy bol vyhladený. S pomocou vyššie uvedeného algoritmu bolo teda možné znížiť stupeň skreslenia trasy a zlepšiť jej vizuálnu kvalitu. Záver V tomto článku sme uvažovali o prístupe ku korekcii GPS súradníc pomocou Kalmanovho filtra. Pomocou vyššie uvedeného algoritmu bolo možné eliminovať najvýraznejšie deformácie trasy, čo demonštruje použiteľnosť tejto metódy na problém vyhladzovania trasy a eliminácie špičiek. Aby sa však ďalej zlepšila kvalita algoritmu, je potrebné ďalšie spracovanie sekvencie súradníc, aby sa zlepšila kvalita algoritmu.

7 eliminácia nadbytočných bodov vznikajúcich pri absencii pohybu pozorovaného objektu. Literatúra 1. Yadav J., Giri R., Meena L. Error handling in GPS data processing // Mausam Vol. 62. Č. 1. P Kalman R. E. A New Approach to Linear Filtering and Prediction Problems // Transactions of the ASME Journal of Basic Engineering Vol. 82. Č. Séria D. P. P. Welch G., Bishop G. Úvod do Kalmanovho filtra: Tech. Rep. TR Dostupné na: prístup Vincenty T. Priame a inverzné riešenia geodetiky na elipsoide s aplikáciou vnorených rovníc // Prehľad prieskumu apr. Vol. 23.Žiadny PP

UDC 519.711.2 Algoritmus na odhad parametrov polohy kozmickej lode pomocou Kalmanovho filtra DI Galkin 1 1 MSTU im. N.E. Bauman, Moskva, 155, Rusko Je uvedený popis konštrukcie filtra Kalman

FEDERÁLNA AGENTÚRA PRE TECHNICKÚ REGULÁCIU A METROLÓGIU NÁRODNÝ ŠTANDARD RUSKEJ FEDERÁCIE GOST R 53608-2009 Globálny navigačný satelitný systém METÓDY A TECHNOLÓGIE IMPLEMENTÁCIE

PROGNÓZA BAYESOVSKÉHO ČASOVÉHO RADU NA ZÁKLADE ŠTÁTNYCH VESMÍRNYCH MODELOV V I Lobach Bieloruská štátna univerzita Minsk Bielorusko E-mail: [e-mail chránený] Zvažuje sa metóda prognózovania

UDC 681.5(07) IDENTIFIKÁCIA NELINEÁRNYCH DYNAMICKÝCH OBJEKTOV V ČASOVEJ DOMÉNE Vyatchennikov, V.V. Kosobutsky, A.A. Nosenko, N.V. Plotnikova Nedostatočné informácie o objektoch pri ich vývoji

Ser. 0,200. Vydanie. 4 SPRAVODAJ KONTROLNÝCH PROCESOV PETERBURSKEJ UNIVERZITY MDT 539.3 VV Karelin TESTOVACIE FUNKCIE V PROBLÉME KONTROLY PROCESU POZOROVANIA. Úvod. Článok je venovaný problému

UDC 63.1/.7 ALGORITY SEKUNDÁRNEHO SPRACOVANIA INFORMÁCIÍ V RADAROVEJ STANICE S RÔZNYMI TYPMI MATICE DYNAMICKÝCH PREPOČTOV PRI URČENÍ SÚRADNICE VÝŠKOVÉHO UHLA Yanitsky А.А. vedecký riaditeľ

Udk 5979 + 5933 A Omarovcov toho istého, nasledujúce [e-mail chránený]Štatistický model pohybu

Úvod do robotiky Prednáška 12. Časť 2. Navigácia a mapovanie. SLAM SLAM Simultaneous Localization And Mapping (simultánna lokalizácia a mapovanie) Úlohou SLAMu je jedna z

Abstrakt prednášky „Lineárne dynamické systémy. Kalmanov filter. na špeciálnom kurze "Štrukturálne metódy analýzy obrazu a signálu" 211 Likbez: niektoré vlastnosti normálneho rozdelenia. Nech je x R d rozdelené

Lokalizačný systém robota založený na hemisférickej kamere Alexander Ovchinnikov, Hoa Phan Katedra rádioelektroniky Tula State University, Tula, Rusko [e-mail chránený], [e-mail chránený]

Proceedings of MAI Issue 84 UDC 57:5198 wwwmairu/science/trudy/ Určenie chýb bezgimbalového inerciálneho navigačného systému v režime rolovania a zrýchlenia Vavilova NB* Golovan AA Kalchenko AO** Moskovsky

# 08, august 2016 UDC 004.93"1 Normalizácia údajov 3D kamier pomocou metódy hlavných komponentov na riešenie problému rozpoznávania póz a správania používateľov inteligentného domu Malykh D.A., študent Rusko,

Národná technická univerzita Ukrajiny "Kyjevský polytechnický inštitút" Katedra prístrojov a systémov orientácie a navigačných smerníc pre laboratórne práce disciplína „Navigačná

UDC 629.78.018:621.397.13 METÓDA PÁROVÝCH VZDIALENOSTÍ V PROBLÉME LETOVÉHO NASTAVENIA ASTRO SNÍMAČOV ORIENTAČNÉHO SYSTÉMU KOZMICKÝCH VOZIDIEL B.M. Suchovilov Ako presnosť a spoľahlivosť astronomických

UDC 629.05 Riešenie problematiky navigácie pomocou popruhového inerciálneho navigačného systému a leteckého signálneho systému Mkrtchyan V.I., študent, odbor „Prístroje a systémy orientácie, stabilizácie a navigácie“

MODEL VIZUÁLNEHO SYSTÉMU ĽUDSKÉHO OPERÁTORA V ROZPOZNÁVANÍ OBRAZU OBJEKTU Yu.S. Gulina, V.Ya. Moskovská štátna technická univerzita Koljuchkin Lomonosov N.E. Bauman, Matematika

RAKETOVÉ A VESMÍRNE NÁSTROJE A INFORMAČNÉ SYSTÉMY 2015, ročník 2, číslo 3, s. 79 83 UDC 681.3.06 SYSTÉMOVÁ ANALÝZA, RIADENIE KOZMICKÝCH LODI, SYSTÉMY SPRACOVANIA INFORMÁCIÍ A TELEMETRIE

Lineárne dynamické systémy. Kalmanov filter. Likbez: niektoré vlastnosti normálneho rozdelenia Hustota rozdelenia.4.3.. -4 x b.5 x b =.7 5 p(x a x b =.7) - x p(x a,x b) p(x a) 4 3 - - -3 x .5

UDC 621.396.671 O. S. Litvinov, A. A. Gilyazov a HODNOTENIE VPLYVU RUŠIVÝCH SKUPÍN NA PRÍJEM UŽITOČNÉHO SIGNÁLU LINEÁRNOU EKVIDISTANTNOU ADAPTÍVNOU ANTÉNOU POMOCOU METÓDY VLASTNEJ SCHÉMY

MDT 681.5.15.44 PROGNÓZA KUSOVÝCH STACIONÁRNYCH PROCESOV E.Yu. Alekseev Zohľadňujú sa diskrétne náhodné procesy obsahujúce parametre, ktoré sa náhle menia v náhodných časoch. Pre

UDC 63966 OPTIMÁLNE LINEÁRNE FILTROVANIE PRE BIELY ŠUM GF Savinov V tomto článku sa získa optimálny algoritmus filtra pre prípad, keď sú vstupné akcie a šumy náhodné Gaussovské

Stanovenie oscilačných pohybov netuhých satelitných prvkov pomocou spracovania obrazu videa D.O. Lazarev Moskovský inštitút fyziky a technológie Vedúci, kandidát fyzikálnych a matematických vied: D.S. Ivanov, Inštitút

MDT 004 O METÓDACH SLEDOVANIA A SLEDOVANIA OBJEKTU VO VIDEOSTREME, AKO SA APLIKÁUJE NA VIDEO ANALYTICKÝ SYSTÉM NA ZBER A ANALÝZU MARKETINGOVÝCH ÚDAJOV Chezganov D.A., Serikov O.N. Juhoruský štát

Elektronický denník"Zborník MAI". Vydanie 66 www.ma.u/scence/tud/ UDC 69.78 Upravený navigačný algoritmus na určenie polohy satelitu pomocou signálov GS/GLONASS Kurshin A.V.

MDT 621.396.96 Skúmanie algoritmu spájania a potvrdenia trajektórií podľa kritéria M z N Černovej TS, študentka katedry "Rádioelektronické systémy a zariadenia", Rusko, 105005, Moskva N.E.

TEÓRIA A PRAX NAVIGAČNÝCH ZARIADENÍ A SYSTÉMOV

6. prednáška Charakteristika portfólií V predchádzajúcich prednáškach sa opakovane používal pojem „portfólio“.

IDENTIFIKÁCIA ČASOVÉHO RADU MEZIER NA ZÁKLADE ŠTÁTNYCH VESMÍRNYCH MODELOV R. I. Merkulov V. I. Lobach Bieloruská štátna univerzita Minsk Bielorusko e-mail: [e-mail chránený] [e-mail chránený]

AUTOMATICKÉ OVLÁDACIE ZARIADENIA A SYSTÉMY

Zborník MAI. Vydanie 89 UDC 629.051 www.mai.ru/science/trudy/ Kalibrácia pripútaného inerciálneho navigačného systému pri otáčaní sa vertikálna os Matasov A.I.*, Tichomirov V.V.** Moskovskij

Analytická geometria Modul 1 Maticová algebra Vektorová algebra Text 4 ( samostatné štúdium) Abstrakt Lineárna závislosť vektorov Kritériá pre lineárnu závislosť dvoch, troch a štyroch vektorov

MDT 62 396,26 L.A. Podkolzina, K. Drugov ALGORITHMY SPRACOVANIA INFORMACIÍ V NAVIGAČNÝCH SYSTÉMOCH POZEMNÝCH OBJEKTOV PRE KANÁL URČOVANIA POLOHOVÝCH SÚRADNÍC Na určenie súradníc a parametrov

ŠTATISTICKÁ ANALÝZA PARAMETRICKÉHO ČASOVÉHO RADU PARAMETROV NA ZÁKLADE ŠTÁTNYCH PRIESTOROVÝCH MODELOV SV Lobach Bieloruská štátna univerzita Minsk, Bielorusko е-mail: [e-mail chránený]

Matematické metódy spracovania údajov MDT 6.39 S. Ya. Zhuk.. Kozheshkurt.. Yuzefovich National Technical University of Ukraine "KP" ave. Pobedy 37 356 Kyjev Ukrajina Inštitút problémov s registráciou informácií NAS

Konštrukcia statiky MM technologických objektov Pri štúdiu statiky technologických objektov sa najčastejšie stretávame s objektmi s nasledujúcimi typmi blokových schém (obr.: O s jedným vstupom x a jedným

Odhad parametrov polohy kozmickej lode pomocou Kalmanovho filtra Študent, Katedra automatických riadiacich systémov: D.I. Galkin Vedecký poradca: A.A. Karpunin, Ph.D., docent

5. Meleshko V.V. Strapdown inerciálne navigačné systémy: Učebnica. príspevok / V.V. Meleshko, O.I. Nesterenko. Kirovograd: POLYMED-Service, 211. 172 s. Uzávierka redakcie 17. apríla 212 Kostyuk

MDT 004.896 Aplikácia geometrických transformácií na anamorfizáciu obrazu Kanev AI, špecialista Rusko, 105005, Moskva, MSTU im. N.E. Bauman, Katedra systémov spracovania informácií a riadenia

4. Metódy Monte Carlo 1 4. Metódy Monte Carlo Na simuláciu rôznych fyzikálnych, ekonomických a iných efektov sa široko používajú metódy nazývané metódy Monte Carlo. Vďačia za svoje meno

Pásmová filtrácia 1 Pásmová filtrácia V predchádzajúcich častiach sme uvažovali o filtrovaní rýchlych variácií signálu (vyhladzovanie) a pomalých variácií signálu (detrending). Niekedy je potrebné zvýrazniť

[POZNÁMKY] Tento článok vysvetľujúci základy Kalmanovho filtra pomocou jednoduchej a intuitívnej derivácie Ramseyho Farahera poskytuje jednoduché a intuitívne odvodenie Kalmanovho filtra na účely výučby.

MDT 004.932 Algoritmus klasifikácie odtlačkov prstov D.S. Lomov, študent Rusko, 105005, Moskva, MSTU im. N.E. Bauman, oddelenie "Počítačový softvér a informačné technológie" Vedúci:

Prednáška NUMERICKÁ CHARAKTERISTIKA SYSTÉMU DVOCH NÁHODNÝCH PREMENNÝCH - ROZMERNÝ NÁHODNÝ VEKTOR ÚČEL PREDNÁŠKY: určiť číselné charakteristiky sústavy dvoch náhodných veličín: počiatočný a centrálny moment, kovariancia

Dynamika pôrodnosti v Čuvašskej republike

V ROKU 1990-5548 Elektronika a riadiace systémy. 2011. 4(30) 73 UDC656.7.052.002.5:681.32(045) V. M. Sineglazov, doktor inžinierstva. Sci., prof., Sh. I. Askerov OPTIMÁLNE KOMPLEXNÉ SPRACOVANIE ÚDAJOV V NAVIGÁCII

MDT 004.896 Vlastnosti implementácie algoritmu na zobrazenie výsledkov anamorfizácie Kanev AI, špecialista Rusko, 105005, Moskva, MSTU im. N.E. Bauman, odbor „Systémy spracovania informácií a

177 UDC 658.310.8: 519.876.2 POUŽITIE PRESNOSNOSTI ODHADU PRI REZERVÁCII SNÍMAČOV L.I. Luzina Článok sa zaoberá možným prístupom k získaniu novej schémy redundancie senzorov. Tradičné

ZBIERKA VEDECKÝCH PRÁC NSTU. 28,4 (54). 37 44 MDT 59.24 O KOMPLEXE PROGRAMOV NA RIEŠENIE PROBLÉMU IDENTIFIKÁCIE LINEÁRNYCH DYNAMICKÝCH DISKRÉTNYCH STACIONÁRNYCH OBJEKTOV G.V. TROSHINA Uvažovalo sa o súbore programov

MDT 625.1:519.222:528.4 S.I. Dolganyuk S.I. Dolganyuk, 2010 ZVYŠOVANIE PRESNOSTI NAVIGAČNÉHO RIEŠENIA PRI UMIESŇOVANÍ POSUNOVACÍCH LOKOMOTÍV POMOCOU VYUŽITIA MODELOV DIGITÁLNEHO VÝVOJA TRATE

UDC 531.1 PRISPÔSOBENIE FILTRA KALMAN NA POUŽITIE S MIESTNYMI A GLOBÁLNYMI NAVIGAČNÝMI SYSTÉMAMI A.N. Zabegaev ( [e-mail chránený]) V.E. Pavlovský ( [e-mail chránený]) Ústav aplikovanej matematiky.

AUTOMATIZÁCIA A RIADENIE MDT 68.58.3 AG Shpektorov, VT Fam V. I. Ulyanova (Lenina) Analýza aplikácie mikromechaniky

ZÁKLADY REGRESNEJ ANALÝZY KONCEP KOrelačnej A REGRESNEJ ANALÝZY Na riešenie problémov ekonomickej analýzy a prognózovania sa často používajú štatistické, reportovacie alebo pozorovateľné údaje.

Prednáška 4. Riešenie sústav lineárnych rovníc jednoduchými iteráciami. Ak má systém veľký rozmer (6 rovníc) alebo je matica systému riedka, na riešenie sú efektívnejšie nepriame iteračné metódy.

58 vedecká konferencia Moskovský inštitút fyziky a technológie Sekcia dynamiky kozmickej lode a riadenia pohybu Systém na určovanie pohybu modelov riadiacich systémov na aerodynamickom stole pomocou videokamery

Prednáška 3 5. METÓDY APROXIMÁCIE FUNKCIÍ FORMULÁCIA PROBLÉMU Uvažuje sa s tabuľkovými funkciami mriežky [ a b] y 5 zadefinovanými v uzloch mriežky Ω. Každá sieť je charakterizovaná krokmi h nerovnomerného alebo h

1. Numerické metódy riešenia rovníc 1. Sústavy lineárnych rovníc. 1.1. priame metódy. 1.2. iteračné metódy. 2. Nelineárne rovnice. 2.1. Rovnice s jednou neznámou. 2.2. Sústavy rovníc. jeden.

MDT 621.396 VYŠETROVANIE ALGORITMOV SEKUNDÁRNEHO SPRACOVANIA INFORMÁCIÍ VIACERÉHO RADAROVÉHO SYSTÉMU PRE VÝŠKOVÝ UHLOVÝ KANÁL Borisov AN, Glinchenko VA, Nazarov AA, Islamov RV, Suchkov PV. Vedecký

Téma Numerické metódy lineárnej algebry - - Téma Numerické metódy lineárnej algebry Klasifikácia Lineárna algebra má štyri hlavné sekcie: Riešenie systémov lineárnych algebraických rovníc (SLAE)

MDT 004.352.242 Rekonštrukcia rozmazaných obrazov riešením integrálnej rovnice konvolučného typu Ivannikova IA, študent Rusko, 105005, Moskva, MSTU im. N.E. Bauman, odbor „Systémy automat

AEROGRAVIMETRICKÝ PRIESKUM V ŠTANDARDNOM REŽIME PREVÁDZKY GPS Mogilevsky V.Ye. JSC “GNPP “Aerogeofizika”

ANALÝZA AKUSTICKÝCH SIGNÁLOV NA ZÁKLADE KALMANOVEJ FILTRAČNEJ METÓDY Gurov, P.G. Žiganov, A.M. Ozersky Vlastnosti dynamického spracovania stochastických signálov pomocou diskrétnych

UDK AA Minko IDENTIFIKÁCIA LINEÁRNEHO OBJEKTU PODĽA ODPOVEDE NA HARMONICKÝ SIGNÁL

PREDNÁŠKA. Odhad komplexnej amplitúdy signálu. Odhad času oneskorenia signálu. Odhad frekvencie signálu s náhodnou fázou. Spoločný odhad času oneskorenia a frekvencie signálu s náhodnou fázou.

Výpočtové technológie Ročník 18, 1, 2013 Identifikácia parametrov procesu anomálnej difúzie na základe diferenčných rovníc AS Ovsienko Samara State Technical University, Rusko e-mail:

1 PROGNÓZA TRHOVÝCH PODMIENOK PETROCHEMICKÝCH PODNIKOV Kordunov D.Yu., Bityutsky S.Ya. Úvod. V moderných ekonomických podmienkach, ktoré sa vyznačujú prudkým rozvojom globálnej integrácie

Úloha simultánnej lokalizácie a mapovania (SLAM) Robot School-2014 Andrey Antonov robotosha.ru 10. október 2014 Plán 1 Základy SLAM 2 RGB-D SLAM 3 Robot Andrey Antonov (robotosha.ru) Úloha SLAM

MDT 004.021 T. N. Romanova, A. V. Sidorin, V. N. Solyakov a K. V. Kozl o v SINTEZ MONOCHROMNÉHO OBRAZU Z KONŠTRUKCIE VIACROHODNÝCH PALIET POMOCOU RIEŠENIA ROVNICE JEDU

Národná technická univerzita Ukrajiny "Kyjevský polytechnický inštitút" Katedra prístrojov a systémov orientácie a navigácie Pokyny pre laboratórne práce v odbore "Navigácia"

Digitálne spracovanie signálu /9 MDT 69,78 ANALYTICKÁ METÓDA VÝPOČTU CHYB URČOVANIA UHOLOVEJ ORIENTÁCIE ZO SIGNÁLOV SYSTÉMOV SATELITNEJ RÁDIONALIZÁCIE Aleshechkin А.М. Úvod Režim definície

VLASTNOSTI TVORENIA POČÍTAČOVÉHO MODELU DYNAMICKÉHO OPTO-ELEKTRONICKÉHO SYSTÉMU Pozdnyakova N.S., Torshina I.P. Moskovská štátna univerzita geodézie a kartografie Fakulta optických informácií

Zborník ISA RAS 009. T. 46 III. APLIKOVANÉ PROBLÉMY DISTRIBUOVANÉHO VÝPOČTU Stacionárne stavy v nelineárnom modeli prenosu náboja v DNA * Stacionárne stavy v nelineárnom modeli prenosu náboja v DNA

Obr.1

Dvojica, ktorú hľadáme, teda leží niekde na tejto priamke. Opakujem, je nemožné vybrať zo všetkých týchto možností tú dvojicu, ktorá skutočne existovala - ktorá dala číslo 12, bez toho, aby sme mali nejaké ďalšie stopy. však v situácii, pre ktorú bol vynájdený Kalmanov filter, existujú také náznaky. O náhodných číslach je niečo známe vopred. Známy je tam najmä takzvaný distribučný histogram pre každú dvojicu čísel. Zvyčajne sa získa po dostatočne dlhých pozorovaniach spádu týchto veľmi náhodných čísel. To znamená, že napríklad zo skúseností je známe, že v 5 % prípadov zvyčajne vypadne dvojica x=1, y=8 (túto dvojicu označíme takto: (1,8)), v 2 % prípadov pár x=2, y=3 ( 2,3), v 1 % prípadov pár (3,1), v 0,024 % prípadov pár (11,1) atď. Tento histogram je opäť nastavený pre všetky páryčísla, vrátane tých, ktoré sú sčítané do 12. Teda pre každú dvojicu, ktorej súčet je 12, môžeme povedať, že napríklad dvojica (1, 11) vypadne v 0,8 % prípadov, dvojica ( 2, 10) - v 1% prípadov, pár (3, 9) - v 1,5% prípadov atď. Z histogramu teda vieme určiť, v akom percente prípadov je súčet členov dvojice 12. Nech je napríklad v 30 % prípadov súčet 12. A vo zvyšných 70 % padnú zvyšné dvojice out - to sú (1,8), (2, 3), (3,1) atď. - tie, ktoré tvoria iné čísla ako 12. Navyše, nech napríklad dvojica (7,5) vypadne v 27 % prípadov, kým všetky ostatné dvojice, ktoré dávajú spolu 12, vypadnú v 0,024 % + 0,8 % + 1 % + 1,5 % +…= 3 % prípadov. Podľa histogramu sme teda zistili, že čísla dávajúce spolu 12 vypadnú v 30 % prípadov. Zároveň vieme, že ak vypadlo 12, tak najčastejšie (27 % z 30 %) je dôvodom pár (7,5). Teda ak už 12 hodených, môžeme povedať, že v 90% (27% z 30% - alebo, čo je rovnaké, 27 krát z každých 30) je dôvodom hodu 12 pár (7,5). S vedomím, že pár (7.5) je najčastejšie dôvodom na získanie sumy rovnajúcej sa 12, je logické predpokladať, že s najväčšou pravdepodobnosťou teraz vypadol. Samozrejme, stále nie je pravda, že číslo 12 je v skutočnosti tvorené týmto konkrétnym párom, ale nabudúce, ak narazíme na 12 a opäť predpokladáme pár (7,5), tak niekde v 90% prípadov sme 100% správne. Ak však predpokladáme dvojicu (2, 10), budeme mať pravdu iba v 1 % z 30 % prípadov, čo sa rovná 3,33 % správnych tipov v porovnaní s 90 % pri uhádnutí dvojice (7,5). To je všetko - to je zmysel algoritmu Kalmanovho filtra. To znamená, že Kalmanov filter nezaručuje, že sa nepomýli pri určovaní súčtu, ale garantuje, že sa pomýli minimálne toľkokrát (pravdepodobnosť chyby bude minimálna), keďže používa štatistiku. - histogram vypadávania z dvojíc čísel. Treba tiež zdôrazniť, že takzvaná hustota distribúcie pravdepodobnosti (PDD) sa často používa v Kalmanovom filtračnom algoritme. Je však potrebné pochopiť, že význam je rovnaký ako význam histogramu. Histogram je navyše funkcia postavená na základe PDF a je jeho aproximáciou (pozri napríklad ).
V zásade môžeme tento histogram znázorniť ako funkciu dvoch premenných – teda ako akúsi plochu nad rovinou xy. Tam, kde je povrch vyšší, je vyššia aj pravdepodobnosť vypadnutia zodpovedajúceho páru. Obrázok 2 ukazuje takýto povrch.

obr.2

Ako vidíte, nad čiarou x + y = 12 (čo sú varianty párov dávajúce spolu 12) sú povrchové body v rôznych výškach a najvyššia výška je vo variante so súradnicami (7,5). A keď narazíme na sumu rovnajúcu sa 12, v 90% prípadov je príčinou vzniku tejto sumy dvojica (7,5). Tie. práve tento pár, ktorého súčet je 12, má najväčšiu pravdepodobnosť výskytu, za predpokladu, že súčet je 12.
Preto je tu opísaná myšlienka Kalmanovho filtra. Práve na ňom sú postavené najrôznejšie jeho úpravy - jednokrokové, viackrokové rekurentné atď. Pre hlbšie štúdium Kalmanovho filtra odporúčam knihu: Van Tries G. Theory of detection, estimation and modulation.

p.s. Pre tých, ktorí majú záujem o vysvetlenie pojmov matematiky, čo sa nazýva „na prstoch“, môžeme odporučiť túto knihu a najmä kapitoly z jej časti „Matematika“ (samotnú knihu alebo jednotlivé kapitoly si môžete zakúpiť na to).

Wienerove filtre sú najvhodnejšie na spracovanie procesov alebo segmentov procesov ako celku (blokové spracovanie). Sekvenčné spracovanie vyžaduje aktuálny odhad signálu v každom cykle, berúc do úvahy informácie prijaté na vstupe filtra počas procesu pozorovania.

Pri Wienerovom filtrovaní by si každá nová vzorka signálu vyžadovala prepočet váh všetkých filtrov. V súčasnosti sú vo veľkej miere využívané adaptívne filtre, v ktorých je vch nové informácie slúži na priebežnú korekciu vopred vykonaného odhadu signálu (sledovanie cieľa v radare, automatické riadiace systémy v riadení atď.). Obzvlášť zaujímavé sú adaptívne filtre rekurzívneho typu, známe ako Kalmanov filter.

Tieto filtre sú široko používané v regulačných slučkách v automatických regulačných a riadiacich systémoch. Odtiaľ pochádzali, o čom svedčí aj taká špecifická terminológia používaná pri opise ich práce ako štátneho priestoru.

Jednou z hlavných úloh, ktoré je potrebné vyriešiť v praxi neurónových výpočtov, je získanie rýchlych a spoľahlivých algoritmov učenia neurónových sietí. V tomto ohľade môže byť užitočné použiť algoritmus učenia lineárnych filtrov v spätnoväzbovej slučke. Keďže algoritmy učenia majú iteratívny charakter, takýto filter musí byť sekvenčný rekurzívny odhad.

Problém odhadu parametrov

Jedným z problémov teórie štatistických riešení, ktorý má veľký praktický význam, je problém odhadu stavových vektorov a parametrov systémov, ktorý je formulovaný nasledovne. Predpokladajme, že je potrebné odhadnúť hodnotu parametra vektora $X$, ktorý je pre priame meranie nedostupný. Namiesto toho sa meria iný parameter $Z$ v závislosti od $X$. Úlohou odhadu je odpovedať na otázku: čo možno povedať o $X$ vzhľadom na $Z$. Vo všeobecnom prípade postup optimálneho odhadu vektora $X$ závisí od akceptovaného kvalitatívneho kritéria pre odhad.

Napríklad Bayesovský prístup k problému odhadu parametrov vyžaduje úplnú a priori informáciu o pravdepodobnostných vlastnostiach odhadovaného parametra, čo je často nemožné. V týchto prípadoch sa uchyľuje k metóde najmenších štvorcov (LSM), ktorá vyžaduje oveľa menej a priori informácií.

Uvažujme o aplikácii najmenších štvorcov pre prípad, keď je vektor pozorovania $Z$ spojený s vektorom odhadu parametra $X$ lineárnym modelom a v pozorovaní je šum $V$, ktorý nekoreluje s odhadovaný parameter:

$Z = HX + V$, (1)

kde $H$ je transformačná matica opisujúca vzťah medzi pozorovanými hodnotami a odhadovanými parametrami.

Odhad $X$ minimalizujúci štvorcovú chybu je napísaný takto:

$X_(ots)=(H^TR_V^(-1)H)^(-1)H^TR_V^(-1)Z$, (2)

Nech je šum $V$ nekorelovaný, v takom prípade je matica $R_V$ len maticou identity a rovnica odhadu sa stáva jednoduchšou:

$X_(ots)=(H^TH)^(-1)H^TZ$, (3)

Záznam v matricovej forme výrazne šetrí papier, ale pre niekoho môže byť nezvyčajný. Toto všetko ilustruje nasledujúci príklad, prevzatý z monografie Yu.M. Korshunova „Matematické základy kybernetiky“.
Existuje nasledujúci elektrický obvod:

Pozorované hodnoty sú v tomto prípade hodnoty prístroja $A_1 ​​​​= 1 A, A_2 = 2 A, V = 20 B$.

Okrem toho je známy odpor $R = 5$ Ohm. Je potrebné čo najlepšie odhadnúť z hľadiska kritéria minimálnej strednej štvorcovej chyby hodnoty prúdov $I_1$ a $I_2$. Najdôležitejšou vecou je, že existuje určitý vzťah medzi pozorovanými hodnotami (údaje z prístroja) a odhadovanými parametrami. A tieto informácie prichádzajú zvonku.

V tomto prípade ide o Kirchhoffove zákony, v prípade filtrovania (o ktorom bude reč neskôr) - autoregresný model časovej rady, ktorý predpokladá, že aktuálna hodnota závisí od predchádzajúcich.

Takže znalosť Kirchhoffových zákonov, ktorá nie je v žiadnom prípade spojená s teóriou štatistických rozhodnutí, vám umožňuje vytvoriť spojenie medzi pozorovanými hodnotami a odhadovanými parametrami (tí, ktorí študovali elektrotechniku, môžu skontrolovať, zvyšok bude musieť vezmite ich za slovo):

$$z_1 = A_1 = I_1 + \xi_1 = 1 $$

$$z_2 = A_2 = I_1 + I_2 + \xi_2 = 2 $$

$$z_2 = V/R = I_1 + 2 * I_2 + \xi_3 = 4 $$

Toto je vo vektorovej forme:

$$\začiatok(vmatica) z_1\\ z_2\\ z_3 \end(vmatica) = \začiatok(vmatica) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatica) \začiatok(vmatica) I_1\ \ I_2 \end(vmatrix) + \begin(vmatrix) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrix)$$

Alebo $Z = HX + V$, kde

$$Z= \začiatok(vmatica) z_1\\ z_2\\ z_3 \end(vmatica) = \begin(vmatica) 1\\ 2\\ 4 \end(vmatica) ; H= \začiatok(vmatica) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatica) ; X= \začiatok(vmatica) I_1\\ I_2 \end(vmatica) ; V= \begin(vmatrix) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrix)$$

Ak vezmeme do úvahy hodnoty šumu ako navzájom nekorelované, zistíme odhad I 1 a I 2 metódou najmenších štvorcov v súlade so vzorcom 3:

$H^TH= \začiatok(vmatica) 1 & 1& 1\\ 0 & 1& 2 \end(vmatica) \začiatok(vmatica) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatica) = \ begin(vmatrix) 3 & 3\\ 3 & 5 \end(vmatrix) ; (H^TH)^(-1)= \frac(1)(6) \begin(vmatica) 5 & -3\\ -3 & 3 \end(vmatica) $;

$H^TZ= \začiatok(vmatica) 1 & 1& 1\\ 0 & 1& 2 \koniec(vmatica) \začiatok(vmatica) 1 \\ 2\\ 4 \end(vmatica) = \začiatok(vmatica) 7\ \ 10 \end(vmatica) ; X(vmatrix)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) \begin(vmatrix) 7\\ 10 \end(vmatrix) = \frac (1)(6) \begin(vmatrix) 5\\ 9 \end(vmatrix)$;

Takže $ I_1 = 5/6 = 0,833 A$; $ I_2 = 9/6 = 1,5 A$.

Úloha filtrovania

Na rozdiel od problému odhadovania parametrov, ktoré majú pevné hodnoty, v probléme filtrácie je potrebné vyhodnocovať procesy, teda nájsť aktuálne odhady časovo premenného signálu skresleného šumom, a teda nedostupného pre priame meranie. Vo všeobecnom prípade typ filtračných algoritmov závisí od štatistických vlastností signálu a šumu.

Budeme predpokladať, že užitočný signál je pomaly sa meniacou funkciou času a šum je nekorelovaný šum. Použijeme metódu najmenších štvorcov, opäť kvôli nedostatku apriórnych informácií o pravdepodobnostných charakteristikách signálu a šumu.

Najprv získame odhad aktuálnej hodnoty $x_n$ pomocou posledných $k$ hodnôt časového radu $z_n, z_(n-1),z_(n-2)\dots z_(n-( k-1))$. Pozorovací model je rovnaký ako v probléme odhadu parametrov:

Je jasné, že $Z$ je stĺpcový vektor pozostávajúci z pozorovaných hodnôt časového radu $z_n, z_(n-1),z_(n-2)\dots z_(n-(k-1)) $, $V $ – vektor stĺpca šumu $\xi _n, \xi _(n-1),\xi_(n-2)\bodky \xi_(n-(k-1))$, skresľujúci skutočný signál. A čo znamenajú symboly $H$ a $X$? O akom stĺpcovom vektore $X$, napríklad, môžeme hovoriť, ak všetko, čo je potrebné, je poskytnúť odhad aktuálnej hodnoty časového radu? A čo znamená transformačná matica $H$, nie je vôbec jasné.

Všetky tieto otázky môžu byť zodpovedané iba vtedy, ak sa vezme do úvahy koncept modelu generovania signálu. To znamená, že je potrebný nejaký model pôvodného signálu. Je to pochopiteľné, pri absencii apriórnych informácií o pravdepodobnostných charakteristikách signálu a šumu zostáva len predpokladať. Môžete to nazvať veštením na kávovej usadenine, no odborníci uprednostňujú inú terminológiu. V ich sušiči vlasov sa tomu hovorí parametrický model.

V tomto prípade sa hodnotia parametre tohto konkrétneho modelu. Pri výbere vhodného modelu generovania signálu nezabúdajte, že akákoľvek analytická funkcia môže byť rozšírená v Taylorovom rade. Pozoruhodnou vlastnosťou Taylorovho radu je, že tvar funkcie v akejkoľvek konečnej vzdialenosti $t$ od nejakého bodu $x=a$ je jednoznačne určený správaním sa funkcie v nekonečne malom okolí bodu $x=a $ (hovoríme o jeho derivátoch prvého a vyššieho rádu).

Existencia Taylorovho radu teda znamená, že analytická funkcia má vnútornú štruktúru s veľmi silným prepojením. Ak sa napríklad obmedzíme na troch členov série Taylor, potom bude model generovania signálu vyzerať takto:

$x_(n-i) = F_(-i)x_n$, (4)

$$X_n= \begin(vmatrix) x_n\\ x"_n\\ x""_n \end(vmatrix) ; F_(-i)= \begin(vmatrix) 1 & -i & i^2/2\\ 0 & 1 & -i\\ 0 & 0 & 1 \end(vmatica) $$

To znamená, že vzorec 4 s daným poradím polynómu (v príklade je rovný 2) vytvára spojenie medzi $n$-tou hodnotou signálu v časovej sekvencii a $(n-i)$-tou . Odhadovaný stavový vektor teda v tomto prípade zahŕňa okrem samotnej odhadovanej hodnoty aj prvú a druhú deriváciu signálu.

V teórii automatického riadenia by sa takýto filter nazýval astatický filter druhého rádu. Transformačná matica $H$ pre tento prípad (odhad je založený na súčasných a $k-1$ predchádzajúcich vzorkách) vyzerá takto:

$$H= \begin(vmatrix) 1 & -k & k^2/2\\ - & - & -\\ 1 & -2 & 2\\ 1 & -1 & 0,5\\ 1 & 0 & 0 \ end(vmatrix)$$

Všetky tieto čísla sú získané z Taylorovho radu za predpokladu, že časový interval medzi susednými pozorovanými hodnotami je konštantný a rovný 1.

Problém filtrovania sa teda podľa našich predpokladov zredukoval na problém odhadovania parametrov; v tomto prípade sa odhadujú parametre nami prijatého modelu generovania signálu. A vyhodnotenie hodnôt stavového vektora $X$ sa vykonáva podľa rovnakého vzorca 3:

$$X_(ots)=(H^TH)^(-1)H^TZ$$

V skutočnosti sme implementovali proces parametrického odhadu založený na autoregresnom modeli procesu generovania signálu.

Vzorec 3 sa softvérovo jednoducho implementuje, preto je potrebné vyplniť maticu $H$ a vektorový stĺpec pozorovaní $Z$. Takéto filtre sú tzv konečné pamäťové filtre, pretože na získanie aktuálneho odhadu $X_(not)$ používajú posledných $k$ pozorovaní. Pri každom novom kroku pozorovania sa k aktuálnemu súboru pozorovaní pridá nový súbor pozorovaní a starý sa zahodí. Tento proces hodnotenia sa nazýva posuvné okno.

Rastúce pamäťové filtre

Filtre s konečnou pamäťou majú hlavnú nevýhodu v tom, že po každom novom pozorovaní je potrebné prepočítať kompletný prepočet všetkých údajov uložených v pamäti. Okrem toho, výpočet odhadov možno spustiť až po nazhromaždení výsledkov prvých $k$ pozorovaní. To znamená, že tieto filtre majú dlhé trvanie prechodného procesu.

Na odstránenie tohto nedostatku je potrebné prejsť od filtra s trvalou pamäťou na filter s rastúca pamäť. V takomto filtri sa počet pozorovaných hodnôt, ktoré sa majú vyhodnotiť, musí zhodovať s číslom n aktuálneho pozorovania. To umožňuje získať odhady začínajúce od počtu pozorovaní, ktorý sa rovná počtu zložiek odhadovaného vektora $X$. A to je určené poradím prevzatého modelu, teda koľko pojmov z Taylorovho radu je v modeli použitých.

Súčasne, keď sa n zvyšuje, zlepšujú sa vyhladzovacie vlastnosti filtra, to znamená, že sa zvyšuje presnosť odhadov. Priama implementácia tohto prístupu je však spojená so zvýšením výpočtových nákladov. Preto sú rastúce pamäťové filtre implementované ako opakujúci.

Ide o to, že v čase n už máme odhad $X_((n-1)ots)$, ktorý obsahuje informácie o všetkých doterajších pozorovaniach $z_n, z_(n-1), z_(n-2) \dots z_ (n-(k-1))$. Odhad $X_(not)$ sa získa nasledujúcim pozorovaním $z_n$ pomocou informácií uložených v odhade $X_((n-1))(\mbox (ot))$. Tento postup sa nazýva rekurentné filtrovanie a pozostáva z nasledujúcich krokov:

• podľa odhadu $X_((n-1))(\mbox (ots))$ je odhad $X_n$ predpovedaný vzorcom 4 pre $i = 1$: $X_(\mbox (noca priori)) = F_1X_((n-1)ots)$. Toto je a priori odhad;
• podľa výsledkov aktuálneho pozorovania $z_n$ sa tento apriórny odhad mení na pravdivý, teda a posteriori;
• tento postup sa opakuje v každom kroku, počnúc $r+1$, kde $r$ je poradie filtra.

Konečný vzorec rekurzívneho filtrovania vyzerá takto:

$X_((n-1)ots) = X_(\mbox (nocapriori)) + (H^T_nH_n)^(-1)h^T_0(z_n - h_0 X_(\mbox (nocapriori)))$, (6 )

kde pre náš filter druhej objednávky:

Rastúci pamäťový filter, ktorý funguje podľa vzorca 6, je špeciálnym prípadom filtrovacieho algoritmu známeho ako Kalmanov filter.

Pri praktickej implementácii tohto vzorca treba pamätať na to, že apriórny odhad v ňom zahrnutý je určený vzorcom 4 a hodnota $h_0 X_(\mbox (nocapriori))$ je prvou zložkou vektora $X_( \mbox (nocapriori))$.

Rastúci pamäťový filter má jednu dôležitú vlastnosť. Pri pohľade na Formulu 6 je konečné skóre súčtom predpokladaného vektora skóre a korekčného člena. Táto korekcia je veľká pre malé $n$ a znižuje sa, keď sa $n$ zvyšuje, pričom má tendenciu k nule ako $n \rightarrow \infty$. To znamená, že ako n rastie, vyhladzovacie vlastnosti filtra rastú a model v ňom vložený začína dominovať. Ale skutočný signál môže zodpovedať modelu iba na oddelené sekcie, takže presnosť predpovede sa zhoršuje.

Aby sa tomu zabránilo, od niektorých $ n$ sa ukladá zákaz ďalšieho skrátenia opravného termínu. To je ekvivalentné zmene filtračného pásma, to znamená, že pre malé n je filter širokopásmový (menej inerciálny), pre veľké n sa stáva viac zotrvačným.

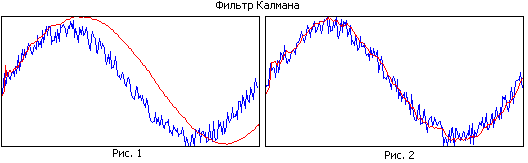
Porovnajte obrázok 1 a obrázok 2. Na prvom obrázku má filter veľkú pamäť, pričom dobre vyhladzuje, no kvôli úzkemu pásmu odhadovaná dráha zaostáva za skutočnou. Na druhom obrázku je pamäť filtra menšia, horšie sa vyhladzuje, no lepšie sleduje skutočnú trajektóriu.

Literatúra

1. Yu.M.Korshunov "Matematické základy kybernetiky"
2. A.V.Balakrishnan "Kalmanova teória filtrácie"
3. V.N. Fomin "Opakujúci sa odhad a adaptívne filtrovanie"
4. C.F.N. Cowen, P.M. Grant "Adaptívne filtre"

Bola vykonaná štúdia o použití Kalmanovho filtra v modernom vývoji komplexu navigačné systémy. Je uvedený a analyzovaný príklad konštrukcie matematického modelu s použitím rozšíreného Kalmanovho filtra na zlepšenie presnosti určenia súradníc bezpilotných lietadiel. Zvažuje sa čiastočný filter. Vyrobené krátka recenzia vedeckých prác použitie tohto filtra na zlepšenie spoľahlivosti a odolnosti voči chybám navigačných systémov. Tento článok nám umožňuje dospieť k záveru, že použitie Kalmanovho filtra v polohovacích systémoch UAV sa praktizuje v mnohých moderných vývojoch. Existuje obrovské množstvo variácií a aspektov tohto použitia, ktoré tiež poskytujú hmatateľné výsledky pri zlepšovaní presnosti, najmä v prípade zlyhania štandardných satelitných navigačných systémov. Toto je hlavný faktor vplyvu tejto technológie na rôzne vedecké oblasti súvisiace s vývojom presných navigačných systémov odolných voči poruchám pre rôzne lietadlá.

Kalmanov filter

navigácia

bezpilotné lietadlo (UAV)

1. Makarenko G.K., Aleshechkin A.M. Skúmanie algoritmu filtrovania pri určovaní súradníc objektu zo signálov satelitných rádiových navigačných systémov Doklady TUSUR. - 2012. - Číslo 2 (26). - S. 15-18.

2. Bar-Shalom Y., Li X. R., Kirubarajan T. Odhad s aplikáciami

na sledovanie a navigáciu // Teória Algoritmy a softvér. - 2001. - Zv. 3. - S. 10-20.

3. Bassem I.S. Navigácia bezpilotných lietadiel (UAV) založená na videní (VBN) // UNIVERZITA V CALGARY. - 2012. - Zv. 1. - S. 100-127.

4. Conte G., Doherty P. Integrovaný navigačný systém UAV založený na porovnávaní leteckých snímok // Aerospace Conference. - 2008. -Zv. 1. - S. 3142-3151.

5. Guoqiang M., Drake S., Anderson B. Návrh rozšíreného kalmanovho filtra pre uav lokalizáciu // In Information, Decision and Control. - 2007. - Zv. 7. – S. 224–229.

6. Optimalizácia trajektórie Ponda S.S pre lokalizáciu cieľa pomocou malých bezpilotných vzdušných prostriedkov // Massachusetts Institute of Technology. - 2008. - Zv. 1. - S. 64-70.

7. Wang J., Garrat M., Lambert A. Integrácia gps/ins/vision senzorov na navigáciu bezpilotných vzdušných prostriedkov // IAPRS&SIS. - 2008. - Zv. 37. – S. 963-969.

Jednou z naliehavých úloh modernej navigácie bezpilotných lietadiel (UAV) je úloha zvýšiť presnosť určovania súradníc. Tento problém je vyriešený použitím rôznych možností integrácie navigačných systémov. Jedným z moderných variantov integrácie je kombinácia navigácie gps/glonass s rozšíreným Kalmanovým filtrom (Extended Kalmanfilter), rekurzívne odhadujúca presnosť pomocou neúplných a zašumených meraní. V súčasnosti existujú a vyvíjajú sa rôzne variácie rozšíreného Kalmanovho filtra, vrátane rôznorodého množstva stavových premenných. V tejto práci ukážeme, aké efektívne môže byť jeho využitie v modernom vývoji. Uvažujme o jednej z charakteristických reprezentácií takéhoto filtra.

Zostavenie matematického modelu

V tomto príklade budeme hovoriť len o pohybe UAV v horizontálnej rovine, inak budeme uvažovať o takzvanom 2d lokalizačnom probléme. V našom prípade je to odôvodnené skutočnosťou, že pre mnohé prakticky sa vyskytujúce situácie môže UAV zostať približne v rovnakej výške. Tento predpoklad je široko používaný na zjednodušenie modelovania dynamiky lietadla. Dynamický model UAV je daný nasledujúcim systémom rovníc:

kde () - súradnice UAV v horizontálnej rovine ako funkcia času, smeru UAV, uhlovej rýchlosti UAV av pozemnej rýchlosti UAV fungujú a budú sa považovať za konštantné. Sú navzájom nezávislé, so známymi kovarianciami a , rovné a , v tomto poradí a používajú sa na simuláciu zmien zrýchlenia UAV spôsobených vetrom, pilotnými manévrami atď. Hodnoty a sú odvodené od maximálnej uhlovej rýchlosti UAV a experimentálnych hodnôt zmien lineárnej rýchlosti UAV, - symbol Kronecker.

Tento systém rovníc bude približný kvôli nelinearite v modeli a kvôli prítomnosti šumu. Najjednoduchšou aproximáciou je v tomto prípade Eulerova aproximácia. Diskrétny model dynamického pohybového systému UAV je uvedený nižšie.

diskrétny stavový vektor Kalmanovho filtra, ktorý umožňuje aproximáciu hodnoty spojitého stavového vektora. ∆ - časový interval medzi meraniami k a k+1. () a () - sekvencie hodnôt bieleho Gaussovho šumu s nulovým priemerom. Matica kovariancie pre prvú sekvenciu:

Podobne pre druhú sekvenciu:

Po vykonaní príslušných substitúcií v rovniciach systému (2) dostaneme:

Sekvencie a sú navzájom nezávislé. Sú to tiež sekvencie bieleho gaussovského šumu s nulovým priemerom s kovariančnými maticami, resp. Výhodou tohto tvaru je, že ukazuje zmenu diskrétneho šumu medzi každým meraním. V dôsledku toho získame nasledujúci diskrétny dynamický model:

(3)

Rovnica pre:

= + , (4)

kde x a y sú súradnice UAV v časovom bode k a je to Gaussova postupnosť náhodných parametrov s nulovou strednou hodnotou, ktorá sa používa na nastavenie chyby. Predpokladá sa, že táto postupnosť je nezávislá od () a ().

Výrazy (3) a (4) slúžia ako základ pre odhad polohy UAV, kde k-té súradnice získané pomocou rozšíreného Kalmanovho filtra. Modelovanie zlyhania navigačných systémov vo vzťahu k tento typ filter vykazuje značnú účinnosť.

Pre väčšiu názornosť uvádzame malý jednoduchý príklad. Nechajte niektoré UAV lietať rovnomerne, s určitým konštantným zrýchlením a.

Kde x je súradnica UAV v čase t a δ je nejaká náhodná premenná.

Predpokladajme, že máme gps senzor, ktorý prijíma údaje o polohe lietadla. Dovoľte nám predstaviť výsledok modelovania tohto procesu v softvérovom balíku MATLAB.

Ryža. 1. Filtrovanie údajov snímača pomocou Kalmanovho filtra

Na obr. 1 ukazuje, aké efektívne môže byť použitie Kalmanovho filtrovania.

V reálnej situácii však majú signály často nelineárnu dynamiku a abnormálny šum. Práve v takýchto prípadoch sa používa rozšírený Kalmanov filter. V prípade, že rozptyly šumu nie sú príliš veľké (t. j. postačí lineárna aproximácia), aplikácia rozšíreného Kalmanovho filtra poskytuje riešenie problému s vysokou presnosťou. Ak však šum nie je Gaussovský, rozšírený Kalmanov filter nemožno použiť. V tomto prípade sa zvyčajne používa čiastočný filter, ktorý využíva numerické metódy na prevzatie integrálov založených na metódach Monte Carlo s Markovovými reťazcami.

Filter častíc

Predstavme si jeden z algoritmov, ktoré rozvíjajú myšlienky rozšíreného Kalmanovho filtra – čiastočný filter. Čiastočné filtrovanie je suboptimálna metóda filtrovania, ktorá funguje pri kombinovaní Monte Carlo na množine častíc, ktoré predstavujú rozdelenie pravdepodobnosti procesu. Tu je častica prvkom prevzatým z predchádzajúcej distribúcie odhadovaného parametra. Hlavnou myšlienkou čiastočného filtra je, že na vyjadrenie odhadu distribúcie možno použiť veľké množstvo častíc. Čím väčší je počet použitých častíc, tým presnejšie bude súbor častíc reprezentovať predchádzajúce rozdelenie. Časticový filter sa inicializuje vložením N častíc z predchádzajúcej distribúcie parametrov, ktoré chceme odhadnúť. Filtračný algoritmus predpokladá, že tieto častice prechádzajú špeciálny systém a potom váženie pomocou informácií získaných meraním týchto častíc. Výsledné častice a ich pridružené hmotnosti predstavujú zadnú distribúciu hodnotiaceho procesu. Cyklus sa opakuje pre každé nové meranie a hmotnosti častíc sa aktualizujú, aby reprezentovali následné rozdelenie. Jedným z hlavných problémov tradičného prístupu k filtrovaniu častíc je, že výsledkom je zvyčajne niekoľko častíc, ktoré sú veľmi ťažké, na rozdiel od väčšiny ostatných, ktoré majú veľmi nízku hmotnosť. To vedie k nestabilite filtrovania. Tento problém možno vyriešiť zavedením vzorkovacej frekvencie, kde sa odoberie N nových častíc z distribúcie tvorenej starými časticami. Výsledok hodnotenia sa získa získaním vzorky priemernej hodnoty množstva častíc. Ak máme viacero nezávislých vzoriek, potom priemer vzorky bude presným odhadom priemeru, ktorý definuje konečný rozptyl.

Aj keď časticový filter nie je optimálny, potom keďže počet častíc má tendenciu k nekonečnu, účinnosť algoritmu sa blíži k Bayesovskému pravidlu odhadu. Preto je žiaduce mať čo najviac častíc na získanie najlepší výsledok. Bohužiaľ to vedie k silnému nárastu zložitosti výpočtov a následne núti hľadať kompromis medzi presnosťou a rýchlosťou výpočtov. Počet častíc by sa teda mal zvoliť na základe požiadaviek na problém hodnotenia presnosti. Ďalším dôležitým faktorom pre fungovanie časticového filtra je obmedzenie vzorkovacej frekvencie. Ako už bolo spomenuté, vzorkovacia frekvencia je dôležitým parametrom filtrovania častíc a bez nej sa algoritmus nakoniec stane degenerovaným. Myšlienka je taká, že ak sú hmotnosti rozložené príliš nerovnomerne a prah vzorkovania sa čoskoro dosiahne, častice s nízkou hmotnosťou sa vyradia a zvyšná množina vytvorí novú hustotu pravdepodobnosti, pre ktorú je možné odobrať nové vzorky. Výber prahu vzorkovacej frekvencie je pomerne náročná úloha, pretože tiež vysoká frekvencia spôsobuje, že filter je príliš citlivý na šum a príliš nízky spôsobuje veľkú chybu. Ďalším dôležitým faktorom je hustota pravdepodobnosti.

Algoritmus filtrovania častíc vo všeobecnosti vykazuje dobrý výkon pri určovaní polohy pre stacionárne ciele a pre relatívne pomaly sa pohybujúce ciele s neznámou dynamikou zrýchlenia. Vo všeobecnosti je algoritmus filtrovania častíc stabilnejší ako rozšírený Kalmanov filter a menej náchylný na degeneráciu a vážne poruchy. V prípadoch nelineárneho, negaussovského rozdelenia tento algoritmus filtrovanie ukazuje veľmi dobrú presnosť umiestnenia cieľa, zatiaľ čo rozšírený Kalmanov algoritmus filtrovania sa za takýchto podmienok nedá použiť. Medzi nevýhody tohto prístupu patrí vyššia zložitosť v porovnaní s rozšíreným Kalmanovým filtrom, ako aj skutočnosť, že nie je vždy zrejmé, ako zvoliť správne parametre pre tento algoritmus.

Sľubný výskum v tejto oblasti

Použitie modelu Kalmanovho filtra podobného tomu, ktorý sme uviedli, je možné vidieť v , kde sa používa na zlepšenie výkonu integrovaného systému (model GPS + počítačového videnia na prispôsobenie sa geografickej základni) a poruchovú situáciu Simuluje sa aj satelitná navigácia. Pomocou Kalmanovho filtra sa výrazne zlepšili výsledky prevádzky systému v prípade poruchy (napr. chyba pri určovaní výšky sa znížila asi dvojnásobne a chyby pri určovaní súradníc pozdĺž rôznych osí sa znížili takmer 9-krát). Podobné použitie Kalmanovho filtra je uvedené aj v .

Zaujímavý problém z pohľadu súboru metód je riešený v . Používa tiež 5-stavový Kalmanov filter s určitými rozdielmi v zostavovaní modelu. Získaný výsledok prevyšuje výsledok nášho modelu vďaka použitiu dodatočných prostriedkov integrácie (používajú sa fotografie a termosnímky). Aplikácia Kalmanovho filtra v tomto prípade umožňuje znížiť chybu pri určovaní priestorových súradníc daného bodu na hodnotu 5,5 m.

Záver

Na záver poznamenávame, že použitie Kalmanovho filtra v polohovacích systémoch UAV sa praktizuje v mnohých moderných vývojoch. Existuje obrovské množstvo variácií a aspektov tohto použitia, až po súčasné použitie niekoľkých podobných filtrov s rôznymi stavovými faktormi. Jednou z najperspektívnejších oblastí pre vývoj Kalmanových filtrov je práca na vytvorení modifikovaného filtra, ktorého chyby budú reprezentované farebným šumom, čím sa stane ešte cennejším pre riešenie reálnych problémov. V odbore je tiež veľký záujem o čiastočný filter, pomocou ktorého je možné filtrovať negaussovský šum. Táto rôznorodosť a hmatateľné výsledky pri zlepšovaní presnosti, najmä v prípade zlyhania štandardných satelitných navigačných systémov, sú hlavnými faktormi ovplyvňujúcimi túto technológiu v rôznych vedeckých oblastiach súvisiacich s vývojom presných a chybovo odolných navigačných systémov pre rôzne lietadlá.

Recenzenti:

Labunets V.G., doktor technických vied, profesor, profesor katedry teoretické základy Rádiotechnická Uralská federálna univerzita pomenovaná po prvom prezidentovi Ruska B. N. Jeľcin, Jekaterinburg;

Ivanov V.E., doktor technických vied, profesor, prednosta. Katedra technológie a komunikácie, Uralská federálna univerzita pomenovaná po prvom prezidentovi Ruska B. N. Jeľcin, Jekaterinburg.

Bibliografický odkaz