Kombinerad användning av en pid-regulator och ett kalman-filter. Använder ett Kalman-filter för att bearbeta en sekvens av GPS-koordinater. Mätbrus kovariansmatris

Random Forest är en av mina favoritalgoritmer för datautvinning. För det första är den otroligt mångsidig, den kan användas för att lösa både regressions- och klassificeringsproblem. Sök efter anomalier och välj prediktorer. För det andra är detta en algoritm som är riktigt svår att tillämpa felaktigt. Helt enkelt för att den, till skillnad från andra algoritmer, har få anpassningsbara parametrar. Och ändå är det förvånansvärt enkelt i sin essens. Samtidigt är det anmärkningsvärt korrekt.

Vad är tanken med en sådan underbar algoritm? Tanken är enkel: låt oss säga att vi har en väldigt svag algoritm, säg . Om vi ​​gör många olika modeller med den här svaga algoritmen och snittar resultatet av deras förutsägelser, kommer slutresultatet att bli mycket bättre. Detta är den så kallade ensemble learning in action. Random Forest-algoritmen kallas därför "Random Forest", för den mottagna data skapar den många beslutsträd och sedan medelvärdet av resultatet av deras förutsägelser. En viktig punkt här är elementet av slumpmässighet i skapandet av varje träd. När allt kommer omkring är det tydligt att om vi skapar många identiska träd, kommer resultatet av deras medelvärde att ha samma noggrannhet som ett träd.

Hur fungerar han? Anta att vi har lite indata. Varje kolumn motsvarar någon parameter, varje rad motsvarar något dataelement.

Vi kan slumpmässigt välja ett antal kolumner och rader från hela datasetet och bygga ett beslutsträd från dem.

Torsdagen den 10 maj 2012

Torsdagen den 12 januari 2012

Allt började i april 2011 när jag hade en telefonintervju med Zynga. Sedan verkade det hela som något slags spel som inte hade något med verkligheten att göra, och jag kunde inte ens föreställa mig vad det skulle leda till. I juni 2011 kom Zynga till Moskva och genomförde en serie intervjuer, cirka 60 kandidater som klarade en telefonintervju övervägdes och cirka 15 personer valdes ut från dem (jag vet inte det exakta antalet, någon ändrade sig senare, någon vägrade omedelbart). Intervjun visade sig vara förvånansvärt enkel. Inga programmeringsuppgifter för dig, inga intrikata frågor om formen på luckor, främst möjligheten att chatta testades. Och kunskap, enligt min mening, utvärderades endast ytligt.

Och så började bråket. Först väntade vi på resultatet, sedan erbjudandet, sedan godkännandet av LCA, sedan godkännandet av ansökan om visum, sedan dokumenten från USA, sedan linjen vid ambassaden, sedan den extra kontrollen, sedan visumet. Ibland verkade det för mig att jag var redo att släppa allt och göra mål. Ibland tvivlade jag på om vi behöver detta Amerika, för Ryssland är inte heller dåligt. Hela processen tog ungefär ett halvår, till slut, i mitten av december, fick vi visum och började förbereda oss för avresa.

Måndagen var min första dag på det nya jobbet. Kontoret har alla förutsättningar att inte bara arbeta, utan också att leva. Frukostar, luncher och middagar från våra egna kockar, ett gäng varierad mat fylld i alla hörn, gym, massage och även frisör. Allt detta är helt gratis för anställda. Många tar sig till jobbet med cykel och flera rum är utrustade för att förvara fordon. I allmänhet har jag aldrig sett något liknande i Ryssland. Allt har dock sitt pris, vi blev direkt förvarnade om att vi skulle behöva jobba mycket. Vad som är "mycket", enligt deras mått mätt, är inte särskilt tydligt för mig.

Jag hoppas dock att jag, trots mängden arbete, inom överskådlig framtid kommer att kunna återuppta bloggandet och kanske berätta något om det amerikanska livet och att jobba som programmerare i Amerika. Vänta och se. Under tiden önskar jag er alla en god jul och ett gott nytt år så ses vi snart!

resultat<- NULL for(i in (1:length(divs[,1]))){ d <- divs if (d$Divs>0)( försök(( citat<- getSymbols(d$Symbol, src="Finam", from="2010-01-01", auto.assign=FALSE) if (!is.nan(quotes)){ price <- Cl(quotes) if (length(price)>0)(dd<- d$Divs result <- rbind(result, data.frame(d$Symbol, d$Name, d$RegistryDate, as.numeric(dd)/as.numeric(price), stringsAsFactors=FALSE)) } } }, silent=TRUE) } } colnames(result) <- c("Symbol", "Name", "RegistryDate", "Divs") result

transkript

1 # 09, september 2015 UDC Tillämpning av Kalman-filtret för bearbetning av sekvensen av GPS-koordinater Listerenko R.R., Bachelor Ryssland, Moskva, MSTU im. N.E. Bauman, avdelning " programvara datorer och Informationsteknologi» Handledare: Bekasov D.E., assistent Ryssland, Moskva, MSTU im. N.E. Bauman, Institutionen för datorprogramvara och informationsteknik Uppgiften att filtrera GPS-koordinater För närvarande används GPS-spårningstjänster flitigt, vars uppgift är att spåra rutter för observerade objekt för att spara dem och ytterligare reproducera och analysera dem. Men på grund av felet i GPS-sensorn på grund av ett antal orsaker, såsom förlust av signal från satelliten, ändring av geometrin för satelliternas placering, signalreflektioner, beräkningsfel och avrundningsfel, gör det slutliga resultatet inte exakt matcha objektets rutt. Det finns både mindre avvikelser (inom 100 m), som inte hindrar uppfattningen av visuell information om rutten och dess analys, och mycket betydande avvikelser (upp till 1 km, i händelse av satellitsignalförlust och användning av basstationer uppåt till flera tiotals km). För att demonstrera resultatet av algoritmen som presenteras i artikeln används en rutt som innehåller avvikelser från den faktiska platsen som överstiger flera kilometer. För att korrigera sådana fel utvecklas en algoritm som utför transformationen av en sekvens av koordinater. Indata för algoritmen är en sekvens av GPS-koordinater. Varje koordinat innehåller följande information som tas emot från sensorn: Latitud Longitud Azimut i grader Objektets momentana hastighet vid den givna punkten i m/s

2 Möjlig avvikelse av objektets koordinater från det sanna värdet i meter Tidpunkt för mottagning av koordinaten av sensorn Resultatet av algoritmen är en sekvens av koordinater med korrigerad latitud och longitud. Som grund för att konstruera algoritmen beslutades det att använda Kalman-filtret, eftersom det låter dig ta hänsyn till mätfel och fel i en slumpmässig process separat, samt använda hastigheten på objektet som tas emot från sensorn. Byggnad matematisk modell använda Kalman-filtret För att använda Kalman-filtret är det nödvändigt att processen som studeras beskrivs på följande sätt: = + + (1) = + (2) till ett tillstånd. Vektorn beskriver kontrollåtgärderna på processen. Matris B med dimensioner n l mappar vektorn för styråtgärder u till en tillståndsändring s. är en slumpvariabel som beskriver felen i processen som studeras, och ~0, där Q är kovariansmatrisen för processfel. Formel (2) beskriver mätningarna av en slumpmässig process. - vektorn för det uppmätta tillståndet av processen, matrisen H med dimensioner m n avbildar processens tillstånd till mätningen av processen. - en slumpvariabel som karakteriserar mätfelen, och ~0, där P är kovariansmatrisen för mätfel. Eftersom ett objekts rörelseprocess undersöks, kompileras tillståndsekvationen baserat på kroppens rörelseekvation = + +!" #$ % & ". Dessutom finns det ingen ytterligare information om rörelseprocessen, så det antas att kontrollåtgärden är 0. Vektorn = + () *, - tas som tillstånd för processen. +, där x, y - koordinater för objektet, - projektioner av objektets hastighet. Således, för processen under övervägande, har ekvation (1) följande form: = + /!, (3)

3 där = ! = 3! + 7 " 0 ; 6 2: 6 " / = : 6 0: 6 2: 6 0: , (4)!,4, (5) (6) I denna modell betraktas ett objekts acceleration som en slumpmässig fel i processen. Följande antaganden görs: a) Accelerationer längs olika axlar är oberoende slumpvariabler.),* b)

4 = AB = C. C E. = C/!!. /. = /C!!. /. Eftersom komponenterna i vektorn ak (5) är oberoende slumpvariabler, då C!!. = " 0 " G. Därför har formel (7) följande form: = / " (8) Mätvektorn zk för detta problem representeras enligt följande: H I = 0 + J, J (7) 2, (9) där H, I - koordinater för objektet som tas emot från sensorn, J +,J, - hastigheten för objektet som tas emot från sensorn Matris H i formel (2) tas lika med identitetsmatrisen med 4 4 dimensioner, eftersom inom ramverket för denna uppgift anses att mätningen är en linjär kombinationstillståndsvektor och några slumpmässiga fel. Mätfelskovariansmatrisen R antas vara given. alternativ dess beräkning är användningen av data om den uppskattade noggrannheten för mätningen som tas emot från sensorn. Tillämpning av Kalmanfiltret på den konstruerade modellen För att tillämpa filtret måste du introducera följande begrepp: - en uppskattning i efterhand av objektets tillstånd vid tidpunkten k, erhållen från resultaten av observationer fram till och med tiden k. L är den okorrigerade a posteriori uppskattningen av objektets tillstånd vid tidpunkten k. - A posteriori felkovariansmatris, som specificerar en uppskattning av noggrannheten hos den erhållna uppskattningen av tillståndsvektorn och inkluderar en uppskattning av felvarianserna för det beräknade tillståndet och kovariansen, som visar de identifierade sambanden mellan systemets tillståndsparametrar. L är den ojusterade bakre felkovariansmatrisen. Matrisen PO sätts till noll, eftersom det antas att objektets initiala position är känd. Ungdomsvetenskapliga och tekniska bulletinen för federala församlingen, ISSN

5 En iteration av Kalman-filtret består av två steg: extrapolering och korrigering. a) Vid extrapoleringssteget beräknas uppskattningen L från uppskattningen av tillståndsvektorn L och felkovariansmatrisen L enligt följande formler: L =, (10) L =. +, (11) där matrisen Ak är känd från formel (4), beräknas matrisen Qk från formel (8). b) Vid korrektionssteget beräknas förstärkningsmatrisen Kk enligt följande formel: M = L. L. + (12) där R, H antas vara kända. Kk används för att korrigera objekttillståndsuppskattningen L och felkovariansmatrisen L enligt följande: = L + M L, (13) = N M L, (14) där I är identitetsmatrisen. Det bör noteras att för att använda ovanstående förhållanden är det nödvändigt att måttenheterna för objektparametrarna som ingår i beräkningarna är konsekventa. I originaldata anges dock latitud och longitud i vinkelkoordinater och hastighet i metrisk. Dessutom är det också bekvämare att specificera accelerationen för att beräkna processfelet i metriska enheter. För att omvandla hastighet och acceleration till vinkelenheter används Vincentis formler. Resultatet av filtret i fig. 1 visar ett exempel på en rutt före bearbetning. Det kan ses i detta exempel det finns flera koordinater med en hög grad av fel, vilket uttrycks i närvaro av "toppar" av koordinater som avsevärt avlägsnas från huvudvägen. På fig. 2 visar resultatet av filteroperationen med denna rutt.

6 Fig. 1. Objektets rutt Fig. 2. Objektets rutt efter applicering av filtret Som ett resultat finns det praktiskt taget inga "toppar", förutom den största, som var märkbart reducerad, och resten av rutten jämnades ut. Således, med hjälp av ovanstående algoritm, var det möjligt att minska graden av ruttförvrängning och förbättra dess visuella kvalitet. Slutsats I detta dokument har vi övervägt ett tillvägagångssätt för att korrigera GPS-koordinater med hjälp av Kalman-filtret. Med hjälp av ovanstående algoritm var det möjligt att eliminera de mest märkbara ruttförvrängningarna, vilket visar tillämpbarheten av denna metod på problemet med ruttutjämning och toppeliminering. För att ytterligare förbättra kvaliteten på algoritmen krävs emellertid ytterligare bearbetning av sekvensen av koordinater för att förbättra kvaliteten på algoritmen.

7 eliminering av redundanta punkter som uppstår i frånvaro av rörelse av det observerade objektet. Referenser 1. Yadav J., Giri R., Meena L. Felhantering i GPS-databehandling // Mausam Vol. 62. Nej. 1. P Kalman R. E. A New Approach to Linear Filtering and Prediction Problems // Transactions of the ASME Journal of Basic Engineering Vol. 82. Nej. Series D. P.P. Welch G., Bishop G. An Introduction to the Kalman Filter: Tech. Rep. TR Tillgänglig på: nås Vincenty T. Direct and Inverse Solutions of Geodesics on the Ellipsoid with application of nested equations // Survey Review apr. Vol. 23.Ingen PP

UDC 519.711.2 Algoritm för att uppskatta rymdfarkosternas attitydparametrar med hjälp av Kalman-filtret DI Galkin 1 1 MSTU im. N.E. Bauman, Moskva, 155, Ryssland Beskrivningen av konstruktionen av Kalman-filtret ges

FEDERAL BYRÅ FÖR TEKNISK REGLERING OCH METROLOGI RYSKA FEDERATIONENS NATIONELLA STANDARD GOST R 53608-2009 Globalt navigationssatellitsystem METODER OCH TEKNIKER FÖR IMPLEMENTERING

BAYESIAN TIME SERIES PROGNOS BASERAD PÅ STATLIGA RYMDMODELLER V I Lobach Vitryska statsuniversitetet Minsk Vitryssland E-post: [e-postskyddad] Prognosmetoden beaktas

UDC 681.5(07) IDENTIFIERING AV INKELINJÄRA DYNAMISKA OBJEKT I TIDSDOMÄNEN Vyatchennikov, V.V. Kosobutsky, A.A. Nosenko, N.V. Plotnikova Otillräcklig information om objekt när man utvecklar dem

Ser. 0,200 Utgåva. 4 BULLETIN OF ST PETERSBURG UNIVERSITY KONTROLLPROCESSER UDC 539.3 VV Karelin STRAFFUNKTIONER I PROBLEMET MED KONTROLL AV OBSERVATIONSPROCESSEN. Introduktion. Artikeln ägnas åt problemet

UDC 63.1/.7 ALGORITIMER FÖR DEN SEKUNDÄRA BEHANDLING AV INFORMATION I EN RADARSTATION MED OLIKA TYPER AV DEN DYNAMISKA ÅTERBERÄKNINGSMATRISEN FÖR BESTÄMNING AV KOORDINATEN FÖR HÖJDVINKEL Yanitsky А.А. vetenskaplig chef

Udk 5979 + 5933 A av Omarovs av samma, följande [e-postskyddad] Statistisk rörelsemodell

Introduktion till robotik Föreläsning 12. Del 2. Navigering och kartläggning. SLAM SLAM Simultaneous Localization And Mapping (samtidig lokalisering och mappning) SLAMs uppgift är en av

Sammanfattning av föreläsningen ”Linjära dynamiska system. Kalman filter. på specialkursen "Strukturella metoder för bild- och signalanalys" 211 Likbez: några egenskaper hos normalfördelningen. Låt x R d fördelas

Robotlokaliseringssystem baserat på en hemisfärisk kamera Alexander Ovchinnikov, Hoa Phan Institutionen för radioelektronik Tula State University, Tula, Ryssland [e-postskyddad], [e-postskyddad]

Proceedings of MAI Issue 84 UDC 57:5198 wwwmairu/science/trudy/ Bestämning av fel i ett kardanlöst tröghetsnavigeringssystem i taxi- och accelerationsläge Vavilova NB* Golovan AA Kalchenko AO** Moskovsky

# 08, augusti 2016 UDC 004.93"1 Normalisering av 3D-kameradata med hjälp av den huvudsakliga komponentmetoden för att lösa problemet med att känna igen poser och beteenden hos användare av smarta hem Malykh D.A., student Ryssland,

National Technical University of Ukraine "Kyiv Polytechnic Institute" Institutionen för instrument och system för orientering och navigering Riktlinjer för laboratoriearbete disciplin "Navigation

UDC 629.78.018:621.397.13 METODEN FÖR PARAVSTÅND I PROBLEMET MED FLYGJUSTERING AV ASTRO-SENSORER I RYMDFORDONS ORIENTERINGSSYSTEM B.M. Sukhovilov Som noggrannheten och tillförlitligheten av astronomiska

UDC 629.05 Att lösa problemet med navigering med hjälp av ett tröghetsnavigeringssystem och ett luftsignalsystem Mkrtchyan V.I., student, Instrument och system för orientering, stabilisering och navigering

MODELL FÖR DET VISUELLA SYSTEMET HOS EN MÄNNISKA OPERATÖR I OBJEKTBILDIGENTIFIERING Yu.S. Gulina, V.Ya. Kolyuchkin Lomonosov Moscow State Technical University N.E. Bauman, Det matematiska

RAKET- OCH RYMDINSTRUMENT OCH INFORMATIONSSYSTEM 2015, volym 2, nummer 3, sid. 79 83 UDC 681.3.06 SYSTEMANALYS, RYMDFARTSKONTROLL, INFORMATIONSBEHANDLING OCH TELEMETRISYSTEM

Linjära dynamiska system. Kalman filter. Likbez: några egenskaper hos normalfördelningen Distributionsdensitet.4.3.. -4 x b.5 x b =.7 5 p(x a x b =.7) - x p(x a,x b) p(x a) 4 3 - - -3 x .5

UDC 621.396.671 O. S. Litvinov, A. A. Gilyazov en UTVÄRDERING AV STÖRINGSGRUPPERNAS PÅVERKAN PÅ RECEPTIONEN AV EN ANVÄNDBAR SIGNAL AV EN LINJÄR LIKVIDISTANT ADAPTIVA ANTENN MED ANVÄNDNING AV METODENS DIAGRAM

UDC 681.5.15.44 PROGNOS AV STATIONÄRA PROCESSER E.Yu. Alekseev Diskreta slumpmässiga processer som innehåller parametrar som ändras abrupt vid slumpmässiga tidpunkter beaktas. För

UDC 63966 OPTIMAL LINJÄR FILTRERING FÖR ICKE-VITT BULLER GF Savinov I detta dokument erhålls en optimal filteralgoritm för fallet då ingångsåtgärderna och bruset är slumpmässiga Gaussiska

Bestämning av oscillerande rörelser hos icke-styva satellitelement med användning av videobildbehandling D.O. Lazarev Moscow Institute of Physics and Technology Handledare, kandidat för fysiska och matematiska vetenskaper: D.S. Ivanov, Institutet

UDC 004 OM METODER FÖR SPÅRNING OCH SPÅRNING AV ETT OBJEKT PÅ EN VIDEOSTRÖM SOM TILLÄMPAS PÅ ETT VIDEOANALYTIKSYSTEM FÖR INSAMLING OCH ANALYSERING AV MARKNADSDATA Chezganov D.A., Serikov O.N. Sydryska staten

Elektronisk journal"Proceedings of MAI". Utgåva 66 www.ma.u/scence/tud/ UDC 69.78 Modifierad navigationsalgoritm för att bestämma positionen för en satellit med hjälp av GS/GLONASS-signaler Kurshin A.V.

UDC 621.396.96 Undersökning av algoritmen för att länka och bekräfta banor enligt kriteriet M av N Chernova TS, student vid avdelningen "Radioelectronic systems and devices", Ryssland, 105005, Moskva N.E.

TEORI OCH PRAKTIK FÖR NAVIGATIONSANORDNINGAR OCH -SYSTEM

Föreläsning 6 Karakteristika för portföljer I tidigare föreläsningar användes termen "portfölj" upprepade gånger

IDENTIFIERING AV GAP TIME SERIE BASERADE PÅ STATLIGA RYMDMODELLER R. I. Merkulov V. I. Lobach Vitryska statsuniversitetet Minsk Vitryssland e-post: [e-postskyddad] [e-postskyddad]

AUTOMATISKA STYRANORDNINGAR OCH SYSTEM

MAI:s förfarande. Utgåva 89 UDC 629.051 www.mai.ru/science/trudy/ Kalibrering av ett tröghetsnavigeringssystem med fastspännade vid svängning vertikal axel Matasov A.I.*, Tikhomirov V.V.** Moskovsky

Analytisk geometri Modul 1 Matrisalgebra Vektoralgebra Text 4 ( oberoende studie) Abstrakt linjärt beroende av vektorer Kriterier för linjärt beroende av två, tre och fyra vektorer

UDC 62.396.26 L.A. Podkolzina, K. Drugov ALGORITIMER FÖR INFORMATIONSBEHANDLING I NAVIGATIONSSYSTEM FÖR MARKFÖRLIGA OBJEKT FÖR KANALEN FÖR BESTÄMNING AV POSITIONSKORDINATER För att bestämma koordinater och parametrar

STATISTISK ANALYS AV GAP-PARAMETRISK TIDSERIER BASERAD PÅ STATLIGA RYMDMODELLER SV Lobach Belarusian State University Minsk, Vitryssland e-post: [e-postskyddad]

Matematiska metoder för databehandling UDC 6,39 S. Ya. Zhuk.. Kozheshkurt.. Yuzefovich National Technical University of Ukraine "KP" ave. Pobedy 37 356 Kiev Ukraine Institute of Information Registreringsproblem NAS

Konstruktion av MM-statik för tekniska objekt När man studerar statiken för tekniska objekt, påträffas oftast objekt med följande typer av blockdiagram (Fig: O med en ingång x och en

Uppskattning av rymdfarkosternas attitydparametrar med hjälp av Kalman-filtret Student, Institutionen för automatiska styrsystem: D.I. Galkin Vetenskaplig rådgivare: A.A. Karpunin, Ph.D., docent

5. Meleshko V.V. Strapdown tröghetsnavigeringssystem: Lärobok. ersättning / V.V. Meleshko, O.I. Nesterenko. Kirovograd: POLYMED-Service, 211. 172 sid. Deadline för redaktionen 17 april 212 Kostyuk

UDC 004.896 Tillämpning av geometriska transformationer för bildanamorfisering Kanev AI, specialist Ryssland, 105005, Moskva, MSTU im. N.E. Bauman, Institutionen för informationsbehandling och styrsystem

4. Monte Carlo-metoder 1 4. Monte Carlo-metoder För att simulera olika fysiska, ekonomiska och andra effekter används metoder som kallas Monte Carlo-metoder i stor utsträckning. De är skyldiga sitt namn

Bandpassfiltrering 1 Bandpassfiltrering I de föregående avsnitten övervägdes filtrering av snabba signalvariationer (utjämning) och långsamma signalvariationer (avskräckande). Ibland behöver man lyfta fram

[ANMÄRKNINGAR] Genom att förklara grunderna för Kalman-filtret Med Ramsey Farahers enkla och intuitiva härledning ger den här artikeln en enkel och intuitiv härledning av Kalman-filtret, i syfte att lära ut det

UDC 004.932 Fingerprint classification algorithm D.S. Lomov, student Ryssland, 105005, Moskva, MSTU im. N.E. Bauman, avdelning "Datorprogramvara och informationsteknologi" Handledare:

Föreläsning NUMERISKA KARAKTERISTIKA FÖR ETT SYSTEM AV TVÅ Slumpvariabler - DIMENSIONELL Slumpmässig VEKTOR SYFTE MED FÖRELÄSNINGAR: att bestämma de numeriska egenskaperna hos ett system av två slumpvariabler: initiala och centrala moment, kovarians

Födelsetalsdynamiken i Chuvash Republic

IN 1990-5548 Elektronik och styrsystem. 2011. 4(30) 73 UDC656.7.052.002.5:681.32(045) V. M. Sineglazov, doktor i teknik. Sci., prof., Sh. I. Askerov OPTIMA KOMPLEXA DATABEHANDLING I NAVIGATION

UDC 004.896 Funktioner i implementeringen av algoritmen för att visa resultaten av anamorfisering Kanev AI, specialist Ryssland, 105005, Moskva, MSTU im. N.E. Bauman, avdelningen "Informationsbehandlingssystem och

177 UDC 658.310.8: 519.876.2 ANVÄNDNING AV EXAKTHETEN I UPPSKATTNING VID RESERVERA SENSORER L.I. Luzina Artikeln överväger ett möjligt tillvägagångssätt för att få ett nytt sensorredundansschema. Traditionell

SAMLING AV VETENSKAPLIGA VERK AV NSTU. 28,4(54). 37 44 UDC 59.24 OM KOMPLEXET AV PROGRAM FÖR LÖSNING AV PROBLEMET MED IDENTIFIERING AV LINJÄRDYNAMISKA DISKRETTA STATIONÄRA OBJEKT G.V. TROSHINA En uppsättning program övervägdes

UDC 625.1:519.222:528.4 S.I. Dolganyuk S.I. Dolganyuk, 2010 ÖKNING AV NOGGRANNHETEN I NAVIGATIONSLÖSNINGEN I POSITIONERING AV SHUNTERLOKOM GENOM ANVÄNDNING AV MODELLER FÖR DIGITAL SPÅRUTVECKLING

UDC 531.1 ANPASSNING AV KALMAN-FILTERET FÖR ANVÄNDNING MED LOKALA OCH GLOBALA NAVIGATIONSSYSTEM A.N. Zabegaev ( [e-postskyddad]) V.E. Pavlovsky ( [e-postskyddad]) Institutet för tillämpad matematik.

AUTOMATION OCH KONTROLL UDC 68.58.3 AG Shpektorov, VT Fam V. I. Ulyanova (Lenina) Analys av tillämpningen av mikromekaniska

GRUNDLÄGGANDE FÖR REGRESSIONSANALYS KONCEPTET KORRELATION OCH REGRESSIONSANALYS För att lösa problem med ekonomisk analys och prognoser används ofta statistik, rapportering eller observerbara

Föreläsning 4. Lösa linjära ekvationssystem genom enkla iterationer. Om systemet har en stor dimension (6 ekvationer) eller om systemets matris är gles, är indirekta iterativa metoder mer effektiva för att lösa.

58:e Vetenskaplig konferens Moscow Institute of Physics and Technology Sektion för rymdfarkosters dynamik och rörelsekontroll System för att bestämma rörelsen hos styrsystemmodeller på ett aerodynamiskt bord med hjälp av en videokamera

Föreläsning 3 5. METODER FÖR APPROXIMATION AV FUNKTIONER FORMULERING AV PROBLEMET Gridtabellfunktioner [a b] y 5 definierade vid noderna i rutnätet Ω beaktas. Varje nät kännetecknas av steg h av olikformig eller h

1. Numeriska metoder för att lösa ekvationer 1. Linjära ekvationssystem. 1.1. direkta metoder. 1.2. iterativa metoder. 2. Icke-linjära ekvationer. 2.1. Ekvationer med en okänd. 2.2. Ekvationssystem. ett.

UDC 621.396 UNDERSÖKNING AV ALGORITMER FÖR SEKUNDÄR BEHANDLING AV INFORMATION OM FLERA RADARSYSTEM FÖR HÖJDVINKELKANALEN Borisov AN, Glinchenko VA, Nazarov AA, Islamov RV, Suchkov PV. Vetenskaplig

Ämne Numeriska metoder för linjär algebra - - Ämne Numeriska metoder för linjär algebra Klassificering Det finns fyra huvudsektioner av linjär algebra: Lösa system av linjära algebraiska ekvationer (SLAE)

UDC 004.352.242 Rekonstruktion av utsmetade bilder genom att lösa en integralekvation av faltningstypen Ivannikova IA, student Ryssland, 105005, Moskva, MSTU im. N.E. Bauman, avdelningen "System av automatiserade

AEROGRAVIMETRISK UNDERSÖKNING UNDER STANDARD GPS-FUNKTIONSLÄGE Mogilevsky V.Ye. JSC "GNPP "Aerogeofizika"

ANALYS AV AKUSTISKA SIGNALER baserad på KALMAN FILTRERINGSMETOD Gurov, P.G. Zhiganov, A.M. Ozersky Funktionerna för dynamisk bearbetning av stokastiska signaler med hjälp av diskreta

UDC AA Minko IDENTIFIKATION AV ETT LINJÄRT OBJEKT GENOM SVAR PÅ EN HARMONISK SIGNAL

FÖRELÄSNING. Uppskattning av signalens komplexa amplitud. Uppskattning av signalfördröjningstid. Uppskattning av frekvensen för en signal med en slumpmässig fas. Gemensam uppskattning av fördröjningstid och frekvens för en signal med en slumpmässig fas.

Computational technologys Volym 18, 1, 2013 Identifiering av onormala diffusionsprocessparametrar baserade på differensekvationer AS Ovsienko Samara State Technical University, Ryssland e-post:

1 FÖRUTSÄTTNING AV MARKNADSFÖRHÅLLANDEN FÖR PETROKEMISKA FÖRETAG Kordunov D.Yu., Bityutsky S.Ya. Introduktion. I moderna ekonomiska förhållanden, som kännetecknas av den snabba utvecklingen av global integration

Samtidig lokalisering och kartläggningsuppgift (SLAM) Robot School-2014 Andrey Antonov robotosha.ru 10 oktober 2014 Plan 1 SLAM Basics 2 RGB-D SLAM 3 Robot Andrey Antonov (robotosha.ru) SLAM-uppgift

UDC 004.021 T. N. Romanova, A. V. Sidorin, V. N. Solyakov och K. V. Kozl o v SINTEZ AV EN MONOKROM BILD FRÅN EN MULTI-RADIG PALETT KONSTRUKTION SOM ANVÄNDER LÖSNINGEN AV GIFTEKVATIONEN

National Technical University of Ukraine "Kyiv Polytechnic Institute" Institutionen för instrument och system för orientering och navigering Riktlinjer för laboratoriearbete inom disciplinen "Navigation

Digital signalbearbetning /9 UDC 69.78 ANALYTISK METOD FÖR BERÄKNING AV FEL FÖR BESTÄMNING AV vinkelorientering FRÅN SIGNALER FRÅN SATELLITRADIONAVIGATIONSSYSTEM Aleshechkin А.М. Inledning Definitionsläge

EGENSKAPER MED ATT FORMA EN DATORMODEL AV ETT DYNAMISKT OPTOELEKTRONISKA SYSTEM Pozdnyakova N.S., Torshina I.P. Moscow State University of Geodesy and Cartography Fakulteten för optisk information

Handlingar av ISA RAS 009. T. 46 III. TILLÄMPAD PROBLEM MED DISTRIBUERAD DATOR Stationära tillstånd i en olinjär modell av laddningsöverföring i DNA * Stationära tillstånd i en olinjär modell av laddningsöverföring i DNA

Figur 1

Således ligger paret vi letar efter någonstans på denna raka linje. Jag upprepar, det är omöjligt att från alla dessa alternativ välja det par som faktiskt fanns – vilket gav siffran 12, utan att ha några ytterligare ledtrådar. I alla fall, i den situation som Kalman-filtret uppfanns för finns det sådana tips. Det är något känt i förväg om slumptal. I synnerhet är det så kallade distributionshistogrammet för varje par av nummer känt där. Det erhålls vanligtvis efter tillräckligt långa observationer av nedfallet av dessa mycket slumpmässiga siffror. Det vill säga att det till exempel är känt av erfarenhet att i 5 % av fallen faller oftast paret x=1, y=8 ut (vi betecknar detta par enligt följande: (1,8)), i 2 % av fallen par x=2, y=3 ( 2,3), i 1 % av fallen ett par (3,1), i 0,024 % av fallen ett par (11,1), etc. Återigen är detta histogram satt för alla par siffror, inklusive de som summerar till 12. Således, för varje par som summerar till 12, kan vi säga att till exempel paret (1, 11) faller ut i 0,8 % av fallen, paret ( 2, 10) - i 1% av fallen, par (3, 9) - i 1,5% av fallen, etc. Således kan vi avgöra från histogrammet i vilken procent av fallen summan av termerna i ett par är 12. Låt till exempel summan i 30 % av fallen ge 12. Och i de återstående 70 % faller de återstående paren ut - dessa är (1.8), (2, 3), (3,1), etc. - de som summerar till andra tal än 12. Låt dessutom till exempel ett par (7,5) falla ut i 27% av fallen, medan alla andra par som ger totalt 12 faller ut i 0,024% + 0,8% + 1%+1,5%+…=3% av fallen. Så enligt histogrammet fick vi reda på att siffror som ger totalt 12 faller ut i 30 % av fallen. Samtidigt vet vi att om 12 ramlade ut så är orsaken oftast (27% av 30%) ett par (7,5). Det vill säga om redan 12 kastade, kan vi säga att i 90% (27% av 30% - eller, vad är detsamma, 27 gånger av varje 30) är anledningen till kast med 12 ett par (7,5). Att veta att paret (7,5) oftast är orsaken till att summan blir lika med 12, är det logiskt att anta att det med största sannolikhet föll ut nu. Naturligtvis är det fortfarande inte ett faktum att talet 12 faktiskt bildas av just detta par, men nästa gång, om vi stöter på 12, och vi återigen antar ett par (7,5), så är vi någonstans i 90% av fallen 100% rätt. Men om vi antar ett par (2, 10), kommer vi att ha rätt endast 1 % av 30 % av gångerna, vilket är lika med 3,33 % av korrekta gissningar jämfört med 90 % när vi gissar ett par (7,5). Det är allt - det här är poängen med Kalman-filteralgoritmen. Det vill säga, Kalman-filtret garanterar inte att det inte kommer att göra ett misstag vid bestämning av termen med summan, men det garanterar att det kommer att göra ett misstag det minsta antalet gånger (sannolikheten för ett fel kommer att vara minimal), eftersom den använder statistik - ett histogram för att falla ut ur par av siffror. Det bör också betonas att den så kallade sannolikhetsfördelningstätheten (PDD) ofta används i Kalman-filtreringsalgoritmen. Det måste dock förstås att innebörden där är densamma som histogrammets. Dessutom är ett histogram en funktion som bygger på PDF och är dess approximation (se till exempel ).
I princip kan vi avbilda detta histogram som en funktion av två variabler – det vill säga som en slags yta ovanför xy-planet. Där ytan är högre är sannolikheten för att motsvarande par faller ut också högre. Figur 2 visar en sådan yta.

fig.2

Som du kan se, ovanför linjen x + y = 12 (som är varianter av par som ger totalt 12), finns ytpunkter på olika höjder och den högsta höjden finns i varianten med koordinater (7,5). Och när vi stöter på en summa som är lika med 12, är i 90% av fallen paret (7,5) orsaken till att denna summa visas. De där. det är detta par, som summerar till 12, som har störst sannolikhet att inträffa, förutsatt att summan är 12.
Därför beskrivs idén bakom Kalman-filtret här. Det är på den som alla typer av dess modifieringar byggs - enstegs, flerstegs återkommande, etc. För en djupare studie av Kalmanfiltret rekommenderar jag boken: Van Tries G. Theory of detection, estimation and modulering.

p.s. För den som är intresserad av att förklara matematikens begrepp, det som kallas "på fingrarna", kan vi rekommendera den här boken och i synnerhet kapitlen från dess "Matematik"-sektion (du kan köpa själva boken eller enskilda kapitel från Det).

Wienerfilter är bäst lämpade för bearbetning av processer eller segment av processer som helhet (blockbearbetning). Sekventiell bearbetning kräver en aktuell uppskattning av signalen vid varje cykel, med hänsyn tagen till informationen som tas emot vid filteringången under observationsprocessen.

Med Wiener-filtrering skulle varje nytt signalprov kräva omräkning av alla filtervikter. För närvarande används adaptiva filter i stor utsträckning, där inkommande ny information används för kontinuerlig korrigering av en tidigare gjord signaluppskattning (målspårning i radar, automatiska styrsystem i styrning, etc.). Av särskilt intresse är adaptiva filter av den rekursiva typen, kända som Kalman-filtret.

Dessa filter används i stor utsträckning i styrslingor i automatiska regler- och styrsystem. Det är där de kom ifrån, vilket framgår av en sådan specifik terminologi som används för att beskriva deras arbete som det statliga rummet.

En av huvuduppgifterna som måste lösas vid utövandet av neurala datorer är att få snabba och pålitliga inlärningsalgoritmer för neurala nätverk. I detta avseende kan det vara användbart att använda en inlärningsalgoritm av linjära filter i återkopplingsslingan. Eftersom inlärningsalgoritmer är iterativa till sin natur måste ett sådant filter vara en sekventiell rekursiv estimator.

Problem med parameteruppskattning

Ett av problemen med teorin om statistiska lösningar, som är av stor praktisk betydelse, är problemet med att uppskatta systemens tillståndsvektorer och parametrar, vilket är formulerat enligt följande. Antag att det är nödvändigt att uppskatta värdet på vektorparametern $X$, som är otillgänglig för direkt mätning. Istället mäts en annan parameter $Z$, beroende på $X$. Uppskattningens uppgift är att svara på frågan: vad kan man säga om $X$ givet $Z$. I det allmänna fallet beror proceduren för optimal uppskattning av vektorn $X$ på det accepterade kvalitetskriteriet för uppskattningen.

Till exempel kräver den bayesianska metoden för parameteruppskattningsproblemet fullständig a priori-information om de probabilistiska egenskaperna hos den uppskattade parametern, vilket ofta är omöjligt. I dessa fall tillgriper man metoden med minsta kvadrater (LSM), som kräver mycket mindre a priori-information.

Låt oss överväga tillämpningen av minsta kvadrater för det fall då observationsvektorn $Z$ är kopplad till parameteruppskattningsvektorn $X$ genom en linjär modell, och det finns ett brus $V$ i observationen som inte är korrelerad med uppskattad parameter:

$Z = HX + V$, (1)

där $H$ är transformationsmatrisen som beskriver förhållandet mellan de observerade värdena och de uppskattade parametrarna.

Uppskattningen $X$ som minimerar det kvadratiska felet skrivs enligt följande:

$X_(ots)=(H^TR_V^(-1)H)^(-1)H^TR_V^(-1)Z$, (2)

Låt bruset $V$ vara okorrelerat, i vilket fall matrisen $R_V$ bara är identitetsmatrisen, och uppskattningsekvationen blir enklare:

$X_(ots)=(H^TH)^(-1)H^TZ$, (3)

Att spela in i matrisform sparar mycket papper, men kan vara ovanligt för någon. Följande exempel, hämtat från Yu. M. Korshunovs monografi "Mathematical Foundations of Cybernetics", illustrerar allt detta.
Det finns följande elektriska krets:

De observerade värdena i detta fall är instrumentavläsningarna $A_1 ​​= 1 A, A_2 = 2 A, V = 20 B$.

Dessutom är motståndet $R = 5$ Ohm känt. Det krävs att man på bästa sätt uppskattar värdena för strömmarna $I_1$ och $I_2$, utifrån det minsta medelkvadratfelskriteriet. Det viktigaste här är att det finns ett visst samband mellan de observerade värdena (instrumentavläsningar) och de uppskattade parametrarna. Och denna information hämtas utifrån.

I det här fallet är det Kirchhoffs lagar, i fallet med filtrering (vilket kommer att diskuteras senare) - en autoregressiv tidsseriemodell, som antar att det aktuella värdet beror på de tidigare.

Så, kunskap om Kirchhoffs lagar, som inte på något sätt är kopplad till teorin om statistiska beslut, gör att du kan upprätta en koppling mellan de observerade värdena och de uppskattade parametrarna (de som studerade elektroteknik kan kontrollera, resten måste ta deras ord för det):

$$z_1 = A_1 = I_1 + \xi_1 = 1$$

$$z_2 = A_2 = I_1 + I_2 + \xi_2 = 2$$

$$z_2 = V/R = I_1 + 2 * I_2 + \xi_3 = 4$$

Detta är i vektorform:

$$\begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) \begin(vmatrix) I_1\ \ I_2 \end(vmatrix) + \begin(vmatrix) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrix)$$

Eller $Z = HX + V$, där

$$Z= \begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1\\ 2\\ 4 \end(vmatrix) ; H= \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) ; X= \begin(vmatrix) I_1\\ I_2 \end(vmatrix) ; V= \begin(vmatrix) \xi_1\\ \xi_2\\ \xi_3 \end(vmatrix)$$

Med tanke på brusvärdena som okorrelerade med varandra hittar vi uppskattningen av I 1 och I 2 med minsta kvadratmetoden i enlighet med formel 3:

$H^TH= \begin(vmatrix) 1 & 1& 1\\ 0 & 1& 2 \end(vmatrix) \begin(vmatrix) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatrix) = \ begin(vmatrix) 3 & 3\\ 3 & 5 \end(vmatrix) ; (H^TH)^(-1)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) $;

$H^TZ= \begin(vmatrix) 1 & 1& 1\\ 0 & 1& 2 \end(vmatrix) \begin(vmatrix) 1 \\ 2\\ 4 \end(vmatrix) = \begin(vmatrix) 7\ \ 10 \end(vmatris) ; X(vmatrix)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) \begin(vmatrix) 7\\ 10 \end(vmatrix) = \frac (1)(6) \begin(vmatrix) 5\\ 9 \end(vmatrix)$;

Så $I_1 = 5/6 = 0,833 A$; $I_2 = 9/6 = 1,5 A$.

Filtreringsuppgift

Till skillnad från uppgiften att uppskatta parametrar som har fasta värden, krävs det i filtreringsproblemet att utvärdera processer, det vill säga att hitta aktuella uppskattningar av en tidsvarierande signal som är förvrängd av brus och därför otillgänglig för direkt mätning. I det allmänna fallet beror typen av filtreringsalgoritmer på de statistiska egenskaperna hos signalen och bruset.

Vi kommer att anta att den användbara signalen är en långsamt varierande funktion av tiden, och att bruset är okorrelerat brus. Vi kommer att använda minsta kvadratmetoden, återigen på grund av bristen på a priori-information om de probabilistiska egenskaperna hos signalen och bruset.

Först får vi en uppskattning av det aktuella värdet av $x_n$ med de sista $k$-värdena i tidsserien $z_n, z_(n-1),z_(n-2)\dots z_(n-( k-1))$. Observationsmodellen är densamma som i parameteruppskattningsproblemet:

Det är tydligt att $Z$ är en kolumnvektor som består av de observerade värdena av tidsserierna $z_n, z_(n-1),z_(n-2)\dots z_(n-(k-1)) $, $V $ – bruskolumnvektor $\xi _n, \xi _(n-1),\xi_(n-2)\dots \xi_(n-(k-1))$, förvränger den sanna signalen. Och vad betyder symbolerna $H$ och $X$? Vilken typ av kolumnvektor $X$ kan vi till exempel prata om om det enda som behövs är att ge en uppskattning av tidsseriens aktuella värde? Och vad som menas med transformationsmatrisen $H$ är inte alls klart.

Alla dessa frågor kan endast besvaras om konceptet med en signalgenereringsmodell införs i övervägande. Det vill säga, någon modell av den ursprungliga signalen behövs. Detta är förståeligt, i frånvaro av a priori information om de probabilistiska egenskaperna hos signalen och bruset återstår det bara att göra antaganden. Man kan kalla det spådomar på kaffesumpen, men experter föredrar en annan terminologi. I deras hårtork kallas detta en parametrisk modell.

I det här fallet uppskattas parametrarna för just denna modell. När du väljer en lämplig signalgenereringsmodell, kom ihåg att alla analytiska funktioner kan utökas i en Taylor-serie. En slående egenskap hos Taylor-serien är att formen av en funktion på vilket ändligt avstånd $t$ som helst från någon punkt $x=a$ bestäms unikt av funktionens beteende i en oändligt liten omgivning av punkten $x=a $ (vi talar om dess första och högre ordningens derivator).

Således innebär förekomsten av Taylor-serier att den analytiska funktionen har en intern struktur med en mycket stark koppling. Om vi ​​till exempel begränsar oss till tre medlemmar av Taylor-serien, kommer signalgenereringsmodellen att se ut så här:

$x_(n-i) = F_(-i)x_n$, (4)

$$X_n= \begin(vmatrix) x_n\\ x"_n\\ x""_n \end(vmatrix) ; F_(-i)= \begin(vmatrix) 1 & -i & i^2/2\\ 0 & 1 & -i\\ 0 & 0 & 1 \end(vmatrix) $$

Det vill säga, formel 4, med en given ordning av polynomet (i exemplet är det lika med 2), upprättar en koppling mellan $n$-th-värdet för signalen i tidssekvensen och $(n-i)$-th . Således inkluderar den uppskattade tillståndsvektorn i detta fall, förutom själva det uppskattade värdet, signalens första och andra derivata.

I teorin om automatisk styrning skulle ett sådant filter kallas ett andra ordningens astatiskt filter. Transformationsmatrisen $H$ för det här fallet (uppskattningen är baserad på nuvarande och $k-1$ tidigare prov) ser ut så här:

$$H= \begin(vmatrix) 1 & -k & k^2/2\\ - & - & -\\ 1 & -2 & 2\\ 1 & -1 & 0.5\\ 1 & 0 & 0 \ end(vmatrix)$$

Alla dessa siffror erhålls från Taylor-serien, förutsatt att tidsintervallet mellan angränsande observerade värden är konstant och lika med 1.

Således har filtreringsproblemet, under våra antaganden, reducerats till problemet med att uppskatta parametrar; i detta fall uppskattas parametrarna för signalgenereringsmodellen som antagits av oss. Och utvärderingen av värdena för tillståndsvektorn $X$ utförs enligt samma formel 3:

$$X_(ots)=(H^TH)^(-1)H^TZ$$

Faktum är att vi har implementerat en parametrisk uppskattningsprocess baserad på en autoregressiv modell av signalgenereringsprocessen.

Formel 3 är lätt att implementera i mjukvara, för detta måste du fylla i matrisen $H$ och vektorkolumnen för observationer $Z$. Sådana filter kallas ändliga minnesfilter, eftersom de använder de senaste $k$-observationerna för att få den aktuella skattningen $X_(not)$. Vid varje nytt observationssteg läggs en ny uppsättning observationer till den nuvarande uppsättningen av observationer och den gamla kasseras. Denna utvärderingsprocess kallas glidande fönster.

Växande minnesfilter

Filter med ändligt minne har den största nackdelen att efter varje ny observation är det nödvändigt att räkna om en fullständig omräkning av all data som lagras i minnet. Dessutom kan beräkningen av uppskattningar startas först efter att resultaten av de första $k$-observationerna har ackumulerats. Det vill säga att dessa filter har en lång varaktighet av den transienta processen.

För att komma till rätta med denna brist är det nödvändigt att gå från ett filter med permanent minne till ett filter med växande minne. I ett sådant filter måste antalet observerade värden som ska utvärderas matcha numret n för den aktuella observationen. Detta gör det möjligt att få uppskattningar med utgångspunkt från antalet observationer lika med antalet komponenter i den uppskattade vektorn $X$. Och detta bestäms av ordningen på den antagna modellen, det vill säga hur många termer från Taylor-serien som används i modellen.

Samtidigt, när n ökar, förbättras filtrets utjämningsegenskaper, det vill säga att uppskattningarnas noggrannhet ökar. Den direkta implementeringen av detta tillvägagångssätt är dock förknippat med en ökning av beräkningskostnaderna. Därför implementeras växande minnesfilter som återkommande.

Poängen är att vi vid tidpunkten n redan har skattningen $X_((n-1)ots)$, som innehåller information om alla tidigare observationer $z_n, z_(n-1), z_(n-2) \dots z_ (n-(k-1))$. Uppskattningen $X_(not)$ erhålls av nästa observation $z_n$ med hjälp av informationen lagrad i uppskattningen $X_((n-1))(\mbox (ot))$. Denna procedur kallas återkommande filtrering och består av följande:

• enligt uppskattningen $X_((n-1))(\mbox (ots))$, förutsägs uppskattningen $X_n$ av formel 4 för $i = 1$: $X_(\mbox (noca priori)) = F_1X_((n-1 )ots)$. Detta är en uppskattning på förhand;
• enligt resultaten av den aktuella observationen $z_n$ omvandlas denna a priori uppskattning till en sann, det vill säga a posteriori;
• denna procedur upprepas vid varje steg, med start från $r+1$, där $r$ är filterordningen.

Den slutliga rekursiva filtreringsformeln ser ut så här:

$X_((n-1)ots) = X_(\mbox (nocapriori)) + (H^T_nH_n)^(-1)h^T_0(z_n - h_0 X_(\mbox (nocapriori)))$, (6 )

där för vårt andra ordningens filter:

Det växande minnesfiltret, som fungerar enligt formel 6, är ett specialfall av filtreringsalgoritmen som kallas Kalman-filtret.

I den praktiska implementeringen av denna formel måste man komma ihåg att den a priori uppskattningen som ingår i den bestäms av formel 4, och värdet $h_0 X_(\mbox (nocapriori))$ är den första komponenten av vektorn $X_( \mbox (nocapriori))$.

Det växande minnesfiltret har en viktig funktion. Om man tittar på Formel 6 är slutpoängen summan av den förväntade poängvektorn och korrigeringstermen. Denna korrigering är stor för små $n$ och minskar när $n$ ökar, och tenderar till noll som $n \rightarrow \infty$. Det vill säga när n växer växer filtrets utjämningsegenskaper och modellen som är inbäddad i det börjar dominera. Men den verkliga signalen kan motsvara modellen endast på separata avsnitt, så noggrannheten i prognosen försämras.

För att bekämpa detta, med start från några $n$, införs ett förbud mot ytterligare minskning av korrigeringstiden. Detta motsvarar att ändra filterbandet, det vill säga för litet n är filtret mer bredbandigt (mindre tröghet), för stort n blir det trögare.

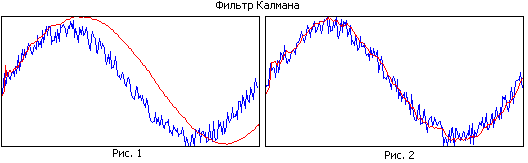
Jämför figur 1 och figur 2. I den första figuren har filtret ett stort minne, samtidigt som det jämnar ut bra, men på grund av det smala bandet ligger den uppskattade banan efter den verkliga. I den andra figuren är filterminnet mindre, det jämnar ut sämre, men det spårar den verkliga banan bättre.

Litteratur

1. Yu.M.Korshunov "Mathematical Foundations of Cybernetics"
2. A.V.Balakrishnan "Kalman filtration theory"
3. V.N. Fomin "Återkommande uppskattning och adaptiv filtrering"
4. C.F.N. Cowen, P.M. Bevilja "Adaptiva filter"

En studie gjordes av användningen av Kalman-filtret i moderna utvecklingar av komplex navigationssystem. Ett exempel på att konstruera en matematisk modell med det utökade Kalman-filtret för att förbättra noggrannheten vid bestämning av koordinaterna för obemannade flygfarkoster ges och analyseras. Delfiltret beaktas. Gjord kort recension vetenskapliga arbeten använder detta filter för att förbättra tillförlitligheten och feltoleransen hos navigationssystem. Denna artikel låter oss dra slutsatsen att användningen av Kalman-filtret i UAV-positioneringssystem praktiseras i många moderna utvecklingar. Det finns ett stort antal variationer och aspekter av denna användning, vilket också ger påtagliga resultat för att förbättra noggrannheten, särskilt i händelse av fel på standardsystem för satellitnavigering. Detta är huvudfaktorn i påverkan av denna teknik på olika vetenskapliga områden relaterade till utvecklingen av noggranna och feltoleranta navigationssystem för olika flygplan.

Kalman filter

navigering

obemannat flygfordon (UAV)

1. Makarenko G.K., Aleshechkin A.M. Undersökning av filtreringsalgoritmen för att bestämma koordinaterna för ett objekt från signalerna från satellitnavigeringssystem Doklady TUSUR. - 2012. - Nr 2 (26). - S. 15-18.

2. Bar-Shalom Y., Li X. R., Kirubarajan T. Uppskattning med applikationer

till spårning och navigering // Teorialgoritmer och programvara. - 2001. - Vol. 3. - S. 10-20.

3. Bassem I.S. Vision based Navigation (VBN) of Unmanned Aerial Vehicles (UAV) // UNIVERSITY OF CALGARY. - 2012. - Vol. 1. - S. 100-127.

4. Conte G., Doherty P. Ett integrerat UAV-navigeringssystem baserat på Aerial Image Matching // Aerospace Conference. - 2008. -Vol. 1. - P. 3142-3151.

5. Guoqiang M., Drake S., Anderson B. Design av ett utökat kalman-filter för UAV-lokalisering // In Information, Decision and Control. - 2007. - Vol. 7. – S. 224–229.

6. Ponda S.S banoptimering för mållokalisering med hjälp av små obemannade flygfarkoster // Massachusetts Institute of Technology. - 2008. - Vol. 1. - S. 64-70.

7. Wang J., Garrat M., Lambert A. Integration av gps/ins/vision-sensorer för att navigera obemannade flygfarkoster // IAPRS&SIS. - 2008. - Vol. 37. – s. 963-969.

En av de brådskande uppgifterna för modern navigering av obemannade flygfarkoster (UAV) är uppgiften att öka noggrannheten vid bestämning av koordinater. Detta problem löses genom att använda olika alternativ för att integrera navigationssystem. Ett av de moderna integrationsalternativen är kombinationen av gps/glonass-navigering med ett utökat Kalmanfilter, som rekursivt uppskattar noggrannheten med hjälp av ofullständiga och bullriga mätningar. För närvarande finns och utvecklas olika varianter av det utökade Kalman-filtret, inklusive ett varierat antal tillståndsvariabler. I detta arbete kommer vi att visa hur effektiv användningen kan vara i modern utveckling. Låt oss överväga en av de karakteristiska representationerna av ett sådant filter.

Att bygga en matematisk modell

I det här exemplet kommer vi bara att prata om UAV:s rörelse i horisontalplanet, annars kommer vi att överväga det så kallade 2d-lokaliseringsproblemet. I vårt fall motiveras detta av det faktum att UAV:en för många praktiskt förekommande situationer kan förbli ungefär på samma höjd. Detta antagande används ofta för att förenkla modellering av flygplansdynamik. Den dynamiska modellen för UAV ges av följande ekvationssystem:

där () - UAV-koordinater i horisontalplanet som en funktion av tid, UAV-riktning, UAV-vinkelhastighet och v UAV-markhastighet, fungerar och kommer att anses vara konstant. De är ömsesidigt oberoende, med kända kovarianser och , lika med respektive , och används för att simulera UAV-accelerationsförändringar orsakade av vind, pilotmanövrar, etc. Värdena och härleds från den maximala vinkelhastigheten för UAV och de experimentella värdena för förändringarna i den linjära hastigheten för UAV, - Kronecker-symbolen.

Detta ekvationssystem kommer att vara ungefärligt på grund av olinjäriteten i modellen och på grund av förekomsten av brus. Den enklaste approximationen i detta fall är Euler approximationen. Den diskreta modellen av det dynamiska rörelsesystemet UAV visas nedan.

diskret tillståndsvektor för Kalman-filtret, som tillåter approximering av värdet av en kontinuerlig tillståndsvektor. ∆ - tidsintervall mellan k och k+1 mätningar. () och () - sekvenser av vita Gaussiska brusvärden med noll medelvärde. Kovariansmatris för den första sekvensen:

På samma sätt, för den andra sekvensen:

Efter att ha gjort lämpliga substitutioner i ekvationerna i system (2) får vi:

Sekvenserna och är ömsesidigt oberoende. De är också noll-medelvärde vita Gaussiska brussekvenser med kovariansmatriser resp. Fördelen med denna form är att den visar förändringen i diskret brus mellan varje mätning. Som ett resultat får vi följande diskreta dynamiska modell:

(3)

Ekvation för:

= + , (4)

där x och y är koordinaterna för UAV vid k-tidpunkten, och är en Gaussisk sekvens av slumpmässiga parametrar med ett nollmedelvärde, som används för att ställa in felet. Denna sekvens antas vara oberoende av () och ().

Uttryck (3) och (4) tjänar som grund för att uppskatta platsen för UAV:en, var k-te koordinater erhålls med det utökade Kalman-filtret. Modellering av navigationssystems fel i förhållande till den här typen filter visar sin betydande effektivitet.

För större tydlighet ger vi ett litet enkelt exempel. Låt en del UAV flyga jämnt, med viss konstant acceleration a.

Där x är koordinaten för UAV vid t-tiden och δ är någon slumpvariabel.

Anta att vi har en gps-sensor som tar emot data om var ett flygplan befinner sig. Låt oss presentera resultatet av att modellera denna process i mjukvarupaketet MATLAB.

Ris. 1. Filtrering av sensoravläsningen med Kalman-filtret

På fig. 1 visar hur effektiv användningen av Kalman-filtrering kan vara.

Men i en verklig situation har signaler ofta icke-linjär dynamik och onormalt brus. Det är i sådana fall som det utökade Kalmanfiltret används. I händelse av att brusspridningarna inte är för stora (dvs en linjär approximation är tillräcklig), ger tillämpningen av det utökade Kalman-filtret en lösning på problemet med hög noggrannhet. Men när bruset inte är Gaussiskt kan det utökade Kalman-filtret inte användas. I det här fallet används vanligtvis ett partiellt filter, som använder numeriska metoder för att ta integraler baserade på Monte Carlo-metoder med Markov-kedjor.

Partikelfilter

Låt oss föreställa oss en av algoritmerna som utvecklar idéerna med det utökade Kalman-filtret - ett delfilter. Partiell filtrering är en suboptimal filtreringsmetod som fungerar när man utför Monte Carlo-kombination på en uppsättning partiklar som representerar sannolikhetsfördelningen för processen. Här är en partikel ett element taget från den tidigare fördelningen av den uppskattade parametern. Huvudidén med ett partiellt filter är att ett stort antal partiklar kan användas för att representera en distributionsuppskattning. Ju större antal partiklar som används, desto mer exakt kommer uppsättningen av partiklar att representera den tidigare fördelningen. Partikelfiltret initieras genom att sätta N partiklar i det från den tidigare fördelningen av parametrarna vi vill uppskatta. Filtreringsalgoritmen förutsätter att dessa partiklar passerar igenom specialsystem, och sedan viktning med hjälp av information erhållen från mätning av dessa partiklar. De resulterande partiklarna och deras associerade massor representerar den bakre fördelningen av uppskattningsprocessen. Cykeln upprepas för varje ny mätning och partikelvikterna uppdateras för att representera den efterföljande fördelningen. Ett av huvudproblemen med den traditionella partikelfiltreringsmetoden är att resultatet vanligtvis är ett fåtal partiklar som är mycket tunga, i motsats till de flesta andra som är mycket lätta. Detta leder till filtreringsinstabilitet. Detta problem kan lösas genom att införa en samplingshastighet, där N nya partiklar tas från en fördelning som består av gamla partiklar. Utvärderingsresultatet erhålls genom att erhålla ett prov av medelvärdet för flertalet partiklar. Om vi ​​har flera oberoende urval, kommer urvalets medelvärde att vara en exakt uppskattning av medelvärdet, som definierar den slutliga variansen.

Även om partikelfiltret inte är optimalt, när antalet partiklar tenderar till oändlighet, närmar sig effektiviteten hos algoritmen den Bayesianska uppskattningsregeln. Därför är det önskvärt att ha så många partiklar som möjligt för att erhålla bästa resultat. Tyvärr leder detta till en kraftig ökning av komplexiteten i beräkningar och tvingar följaktligen fram ett sökande efter en kompromiss mellan noggrannhet och beräkningshastighet. Så antalet partiklar bör väljas baserat på kraven för noggrannhetsbedömningsproblemet. En annan viktig faktor för driften av ett partikelfilter är begränsningen av provtagningshastigheten. Som tidigare nämnts är samplingshastigheten en viktig partikelfiltreringsparameter och utan den kommer algoritmen så småningom att degenereras. Tanken är att om vikterna är för ojämnt fördelade och provtagningströskeln snart nås, så kasseras partiklarna med låg vikt, och den återstående uppsättningen bildar en ny sannolikhetstäthet för vilken nya prover kan tas. Valet av samplingsfrekvenströskeln är en ganska svår uppgift, eftersom också hög frekvens gör att filtret blir för känsligt för brus, och för lågt ger ett stort fel. En annan viktig faktor är sannolikhetstätheten.

Generellt sett visar partikelfiltreringsalgoritmen bra positioneringsprestanda för stationära mål och för relativt långsamt rörliga mål med okänd accelerationsdynamik. Generellt sett är partikelfiltreringsalgoritmen mer stabil än det utökade Kalman-filtret och mindre benägen för degeneration och allvarliga fel. I fall av icke-linjär, icke-gaussisk fördelning denna algoritm filtrering visar en mycket god målplatsnoggrannhet, medan den utökade Kalman-filtreringsalgoritmen inte kan användas under sådana förhållanden. Nackdelarna med detta tillvägagångssätt inkluderar dess högre komplexitet i förhållande till det utökade Kalman-filtret, såväl som det faktum att det inte alltid är självklart hur man väljer rätt parametrar för denna algoritm.

Lovande forskning inom detta område

Användningen av en Kalman-filtermodell, som den vi har angett, kan ses i , där den används för att förbättra prestandan hos ett integrerat system (GPS + datorseende modell för matchning med en geografisk bas), och situationen för fel på satellitnavigeringsutrustning simuleras också. Med hjälp av Kalman-filtret förbättrades resultaten av systemdriften vid fel avsevärt (till exempel minskades felet vid bestämning av höjden med cirka två gånger, och felen vid bestämning av koordinaterna längs olika axlar reducerades nästan 9 gånger). En liknande användning av Kalman-filtret ges också i .

Ett intressant problem ur en uppsättning metoders synvinkel löses i . Den använder också ett 5-läges Kalman-filter, med vissa skillnader i modellbyggandet. Det erhållna resultatet överstiger resultatet av vår modell på grund av användningen av ytterligare metoder för integration (foto och termiska bilder används). Tillämpningen av Kalman-filtret i detta fall gör det möjligt att reducera felet vid bestämning av de rumsliga koordinaterna för en given punkt till ett värde av 5,5 m.

Slutsats

Sammanfattningsvis noterar vi att användningen av Kalman-filtret i UAV-positioneringssystem praktiseras i många moderna utvecklingar. Det finns ett stort antal variationer och aspekter av denna användning, upp till samtidig användning av flera liknande filter med olika tillståndsfaktorer. Ett av de mest lovande områdena för utvecklingen av Kalman-filter är arbetet med att skapa ett modifierat filter, vars fel kommer att representeras av färgbrus, vilket kommer att göra det ännu mer värdefullt för att lösa verkliga problem. Av stort intresse inom tekniken är också ett partiellt filter med vilket icke-Gaussiskt brus kan filtreras. Denna mångfald och påtagliga resultat för att förbättra noggrannheten, särskilt i händelse av fel påm, är de viktigaste faktorerna som påverkar denna teknik inom olika vetenskapliga områden relaterade till utvecklingen av noggranna och feltoleranta navigationssystem för olika flygplan.

Recensenter:

Labunets V.G., doktor i tekniska vetenskaper, professor, professor vid institutionen teoretiska grunder Radio Engineering Ural Federal University uppkallad efter Rysslands första president B.N. Jeltsin, Jekaterinburg;

Ivanov V.E., doktor i tekniska vetenskaper, professor, chef. Institutionen för teknik och kommunikation, Ural Federal University uppkallad efter Rysslands första president B.N. Jeltsin, Jekaterinburg.

Bibliografisk länk